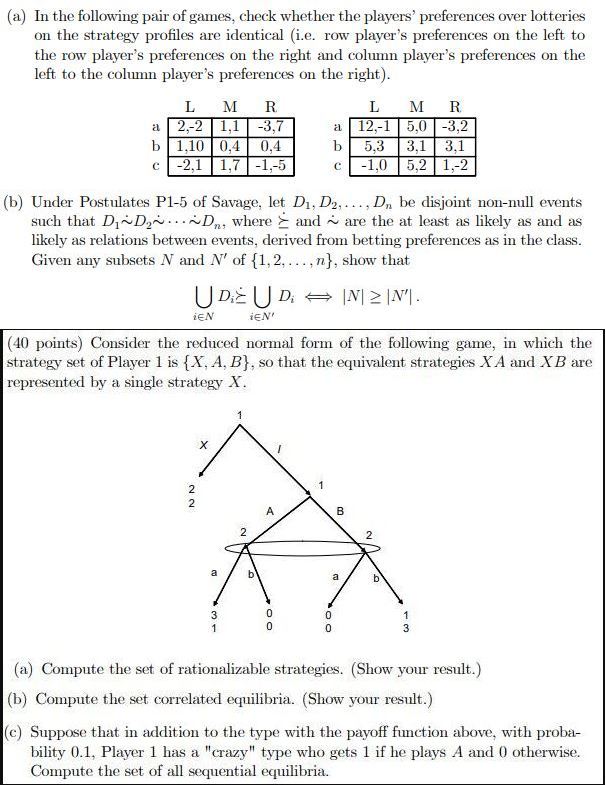
(a) In the following pair of games, check whether the players' preferences over lotteries on the strategy profiles are identical (i.e. row player's preferences on the left to the row player's preferences on the right and column player's preferences on the left to the column player's preferences on the right). L M R L M R 2.-2 1,1 -3,7 12.-1 5.0 -3,2 1,10 0,4 0,4 5.3 3,1 3.1 -2,1 1,7 -1,-5 -1,0 5.2 1,-2 (b) Under Postulates P1-5 of Savage, let D1, D2. .... D, be disjoint non-null events such that Di~Dy...~Dn, where > and ~ are the at least as likely as and as likely as relations between events, derived from betting preferences as in the class. Given any subsets N and N' of {1, 2. ....n}, show that UD UD - IN1 2 IN'. iEN iEN' (40 points) Consider the reduced normal form of the following game, in which the strategy set of Player 1 is {X, A, B}, so that the equivalent strategies X A and X B are represented by a single strategy X. X NO N 2 (a) Compute the set of rationalizable strategies. (Show your result.) (b) Compute the set correlated equilibria. (Show your result.) (c) Suppose that in addition to the type with the payoff function above, with proba- bility 0.1, Player 1 has a "crazy" type who gets 1 if he plays A and 0 otherwise. Compute the set of all sequential equilibria.(30 points) Consider an expected profit maximizing monopolist who faces an uncertain demand. He supplies q units of goods at zero cost and sells it at price e - q, where e is unknown. [The price and the supply level can be negative.] (a) Assuming that # ~ N (y. o'), compute the monopolist's optimal supply q and his expected profit under the optimal supply. (b) Suppose that, through market research, the monopolist can learn about 0. In particular, by investing c', he can learn the value of a random variable Y before choosing his supply q, such that 0 = X + Y, X ~ N (0, 1 - c) and Y ~ N (0, c). How much should the monopolist invest? [Note that the utility function of the monopolist is (0 - q) q - c2.] 3. (40 Minutes - 20 Points) Harvard and MIT are both considering whether to admit a particular student to their economics Ph.D. programs. Assume that MIT has read the student's application carefully and knows the quality q of the student. Assume that Harvard faculty members are too busy to read applications carefully. Instead they must base their decisions on their prior about the student's ability. Harvard's prior is that q may be 1, 2 or 3 and that each of these values is equally likely. Assume that each school must make one of two decisions on the student: admit with financial aid or reject (the student has no source of support and could not attend graduate school without financial aid). The schools make these decisions simultaneously. Assume that each school's payoff in the game is 0 if they do not offer the student admission, -1 if the student is offered admission and turns them down (this is costly both because the school loses prestige and because the slot could have been given to another student), and q - 1.5 if the student is offered admission and decides to come. Assume that if the student is admitted to both schools she chooses to come to MIT with probability 0.65 and to go to Harvard with probability 0.35. In the following questions treat this as a two player game between Harvard (player 1) and MIT (player 2). (a) What type spaces Oj and Oz would you use to represent this situation as a static game of incomplete information? How many elements are in each set? Write down the val- ues of the utility functions w, (a1, 02; 61, 02) for a couple values of i, a1, a2, 01, 02 to illustrate how to compute them. How many pure Bayesian strategies does each player have? (b) What actions are strictly (conditionally) dominated for each possible type of each player? (c) Find the Bayesian Nash equilibrium of this game. (d) Would Harvard be any better off if it could observe MIT's admission decision before making its decision