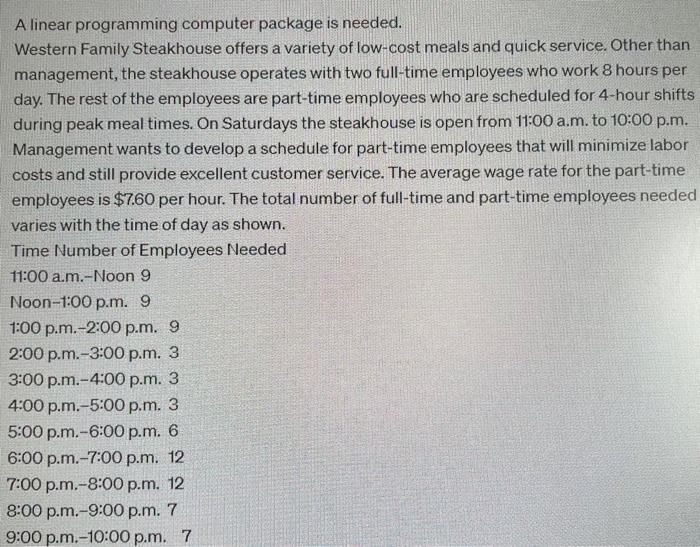
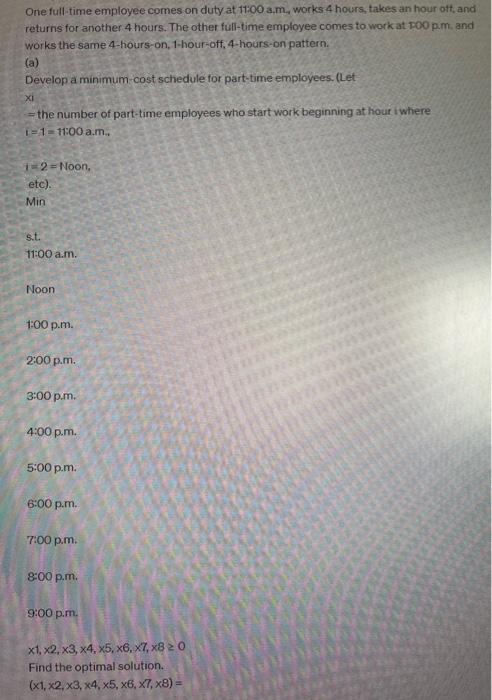
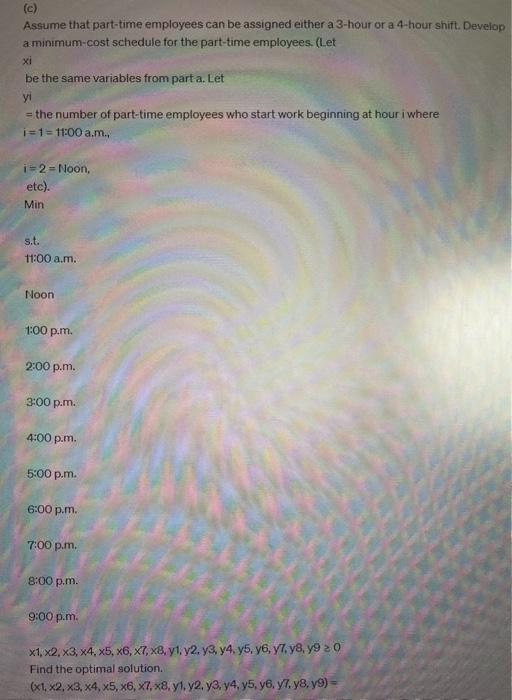
A linear programming computer package is needed. Western Family Steakhouse offers a variety of low-cost meals and quick service. Other than management, the steakhouse operates with two full-time employees who work 8 hours per day. The rest of the employees are part-time employees who are scheduled for 4 -hour shifts during peak meal times. On Saturdays the steakhouse is open from 11:00 a.m. to 10:00 p.m. Management wants to develop a schedule for part-time employees that will minimize labor costs and still provide excellent customer service. The average wage rate for the part-time employees is $7.60 per hour. The total number of full-time and part-time employees needed varies with the time of day as shown. Time Number of Employees Needed 11:00 a.m.-Noon 9 Noon-1:00 p.m. 9 1:00 p.m.-2:00 p.m. 9 2:00 p.m. 3:00 p.m. 3 3:00 p.m. 4:00 p.m. 3 4:00 p.m. 5:00 p.m. 3 5:00 p.m. 6:00 p.m. 6 6:00 p.m.-7:00 p.m. 12 7:00 p.m.-8:00 p.m. 12 8:00 p.m. 9:00 p.m. 7 One full-time employee comes on duty at 11.00a,m, works 4 hours, takes an hour oft, and returns for another 4 hours. The other full-time employee comes to workat poo p.m. and works the same 4-hours-on, 1-hour-off, 4-hours-on pattern. (a) Develop a minimum cost schedule for part-time employees. (Let xi = the number of part-time employees who start work beginning at hour iwhere t=1=1100a.m. 1=2= Noon, etc). Min s.t. 11:00 a.m. Noon 1:00 p.m. 2:00 p.m. 3:00 p.m. 4:00 p.m. 5:00 p.m. 6:00 p.m. 7:00 p.m. 8:00 p.m. 9:00 p.m. x1,2,3,4,5,6,7,80 Find the optimal solution. (12345678)= (b) What is the total payroll (in \$) for the part-time employees? $ How many part-time shifts are needed? (c) Assume that part-time employees can be assigned either a 3-hour or a 4-hour shift. Devel a minimum-cost schedule for the part-time employees. (Let xi be the same variables from parta. Let yi = the number of part-time employees who start work beginning at hour i where i=1=11:00am. i=2= Noon, etc). Min s.t. 11:00 a.m. Noon 1:00 p.m. 2:00 p.m. 3:00 p.m. 4:00 p.m. 5:00 p.m. 6:00 p.m. 7:00 p.m. 8:00 p.m. 9:00 p.m. x1,2,x3,x4,x5,x6,x7,x8,y1,y2,y3,y4,y5,y6,y7,y8,y90 Find the optimal solution. How many part-time shifts are needed, and what is the cost savings (in \$) compared to the previous schedule? part-time shifts needed cost savings \$