Question
A. Listed below are paired data consisting of amounts spent on advertising (in millions of dollars) and the profits (in millions of dollars). Determine if
A. Listed below are paired data consisting of amounts spent on advertising (in millions of dollars) and the profits (in millions of dollars). Determine if there is a significant linear correlation between advertising cost and profit . Use a significance level of 0.01 and round all values to 4 decimal places.
| Advertising Cost | Profit |
|---|---|
| 3 | 25 |
| 4 | 19 |
| 5 | 19 |
| 6 | 21 |
| 7 | 17 |
| 8 | 20 |
Ho:? = 0 Ha:? ? 0
Find the Linear Correlation Coefficient r = __________
Find the p-value p-value = ________
The p-value is
- Less than (or equal to) ??
- Greater than ??
The p-value leads to a decision to
- Reject Ho
- Accept Ho
- Do Not Reject Ho
The conclusion is
- There is a significant linear correlation between advertising expense and profit.
- There is a significant negative linear correlation between advertising expense and profit.
- There is insufficient evidence to make a conclusion about the linear correlation between advertising expense and profit.
- There is a significant positive linear correlation between advertising expense and profit.
B. A study was done to look at the relationship between number of vacation days employees take each year and the number of sick days they take each year. The results of the survey are shown below.
| Vacation Days | 13 | 7 | 7 | 10 | 5 | 11 | 15 | 6 | 1 | 15 | 11 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Sick Days | 1 | 5 | 1 | 0 | 3 | 4 | 0 | 3 | 10 | 0 | 3 |
- Find the correlation coefficient: r=r= Round to 2 decimal places.
- The null and alternative hypotheses for correlation are: H0:H0: ? r ? ? == 0 H1:H1: ? ? ? r ??0 The p-value is: __________ (Round to four decimal places)
- Use a level of significance of?=0.05?=0.05to state the conclusion of the hypothesis test in the context of the study.
- There is statistically significant evidence to conclude that there is a correlation between the number of vacation days taken and the number of sick days taken. Thus, the regression line is useful.
- There is statistically significant evidence to conclude that an employee who takes more vacation days will take fewer sick days than an employee who takes fewer vacation days .
- There is statistically significant evidence to conclude that an employee who takes more vacation days will take more sick days than an employee who takes fewer vacation days.
- There is statistically insignificant evidence to conclude that there is a correlation between the number of vacation days taken and the number of sick days taken. Thus, the use of the regression line is not appropriate.
- r2=__________ (Round to two decimal places)
- Interpretr2:
- There is a 59% chance that the regression line will be a good predictor for the number of sick days taken based on the number of vacation days taken.
- There is a large variation in the number of sick days employees take, but if you only look at employees who take a fixed number of vacation days, this variation on average is reduced by 59%.
- Given any group with a fixed number of vacation days taken, 59% of all of those employees will take the predicted number of sick days.
- 59% of all employees will take the average number of sick days.
- 6. The equation of the linear regression line is: ?y=_______ +______ x (Please show your answers to two decimal places) 7. Use the model to predict the number of sick days taken for an employee who took 4 vacation days this year. Sick Days = _________ (Please round your answer to the nearest whole number.)
- 8. Interpret the slope of the regression line in the context of the question:
- For every additional vacation day taken, employees tend to take on average 0.52 fewer sick days.
- As x goes up, y goes down.
- The slope has no practical meaning since a negative number cannot occur with vacation days and sick days.
- 9. Interpret the y-intercept in the context of the question:
- If an employee takes no vacation days, then that employee will take 7 sick days.
- The best prediction for an employee who doesn't take any vacation days is that the employee will take 7 sick days.
- The y-intercept has no practical meaning for this study.
- The average number of sick days is predicted to be 7.
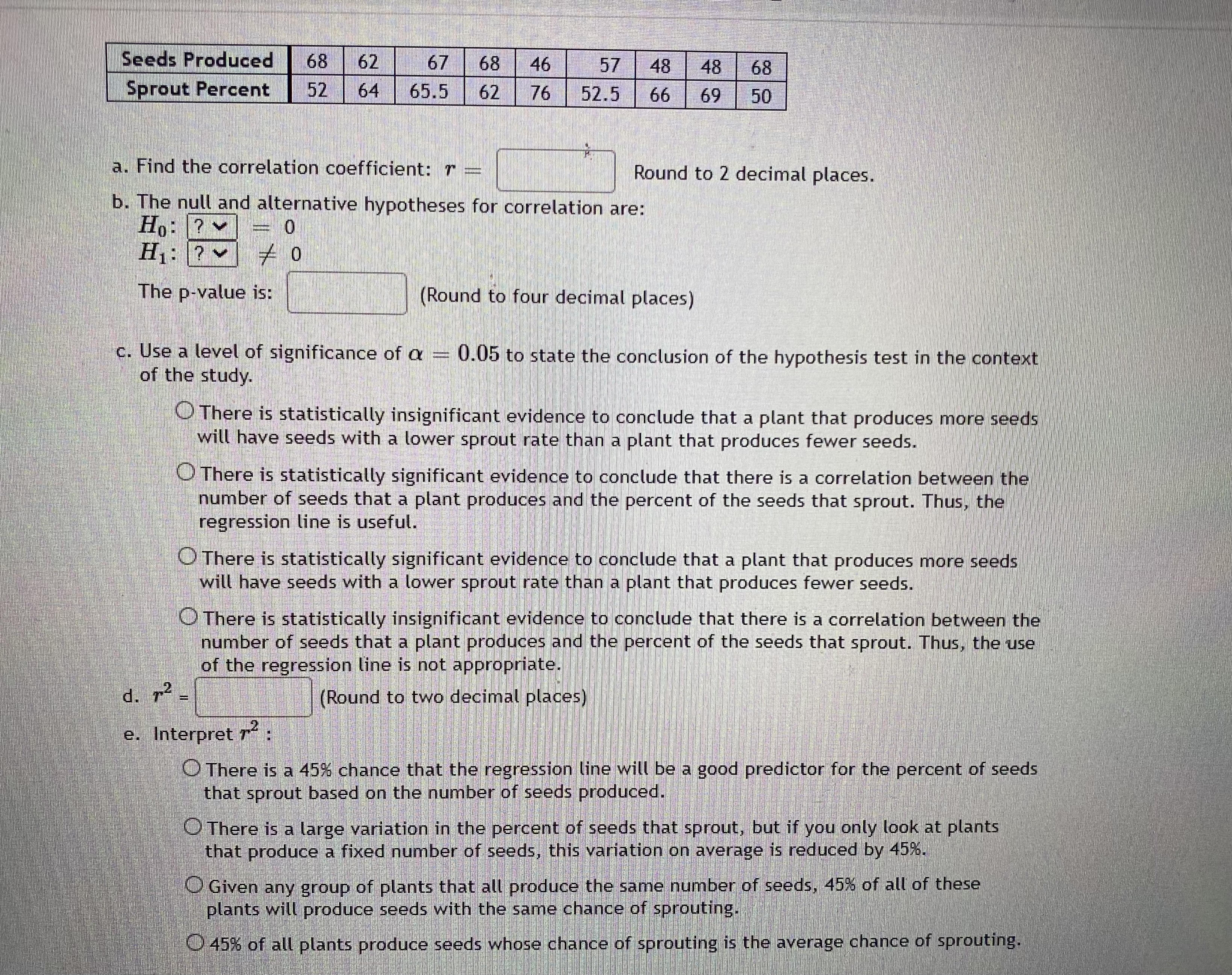
C. A biologist looked at the relationship between number of seeds a plant produces and the percent of those seeds that sprout. The results of the survey are shown below.

Step by Step Solution
There are 3 Steps involved in it
Step: 1

Get Instant Access to Expert-Tailored Solutions
See step-by-step solutions with expert insights and AI powered tools for academic success
Step: 2

Step: 3

Ace Your Homework with AI
Get the answers you need in no time with our AI-driven, step-by-step assistance
Get Started


