A number of stories in the press about the structure of the Internet and the Web have focused on some version of the following question: How far apart are typical nodes in these networks? If you read these stories carefully, you find that many of them are confused about the difference between the diameter of a network and the average distance in a network; they often jump back and forth between these concepts as though theyre the same thing.

As in the text, we say that the distance between two nodes u and v in a graph G = (V , E) is the minimum number of edges in a path joining them; well denote this by dist(u, v). We say that the diameter of G is the maximum distance between any pair of nodes; and well denote this quantity by diam(G).

Lets define a related quantity, which well call the average pairwise distance in G (denoted apd(G)). We define apd(G) to be the average, over all sets of two distinct nodes u and v, of the distance between u and v. 2

That is,

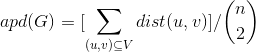
Heres a simple example to convince yourself that there are graphs G for which diam(G) 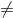apd(G). Let G be a graph with three nodes u, v, w, and with the two edges {u, v} and {v, w}. Then:

diam(G) = dist(u, w) = 2,

while:

apd(G) = [dist(u, v) + dist(u, w) + dist(v, w)]/3 = 4/3.

Of course, these two numbers arent all that far apart in the case of this three-node graph, and so its natural to ask whether theres always a close relation between them. Heres a claim that tries to make this precise.

Claim: There exists a positive natural number c so that for all connected graphs G, it is the case that :

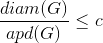
Decide whether you think the claim is true or false, and give a proof of either the claim or its negation.

n2