Answered step by step
Verified Expert Solution
Question
1 Approved Answer
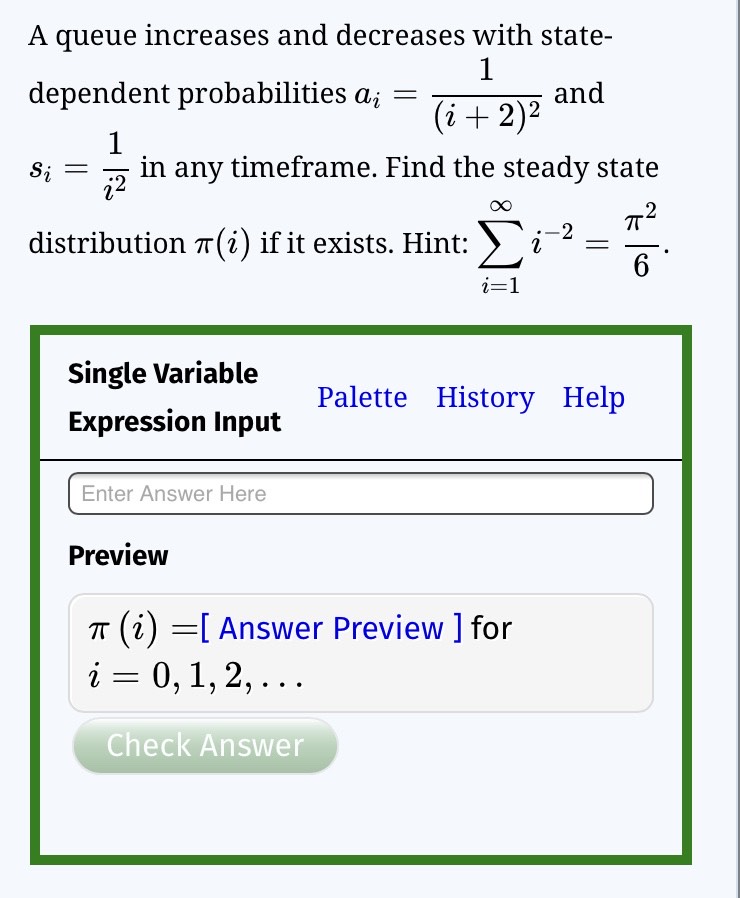
A queue increases and decreases with state-dependent probabilitiesa_i=dfrac{1}{(i+2)^2} a?i ??=?(i+2)?2 ?? ? ?1 ??ands_i=dfrac{1}{i^2} s?i ??=?i?2 ?? ? ?1 ??in any timeframe. Find the steady
A queue increases and decreases with state-dependent probabilitiesa_i=\dfrac{1}{(i+2)^2}
a?i
??=?(i+2)?2
??
?
?1
??ands_i=\dfrac{1}{i^2}
s?i
??=?i?2
??
?
?1
??in any timeframe. Find the steady state distribution\pi(i)
?(i)if it exists. Hint:\displaystyle \sum_{i=1}^{\infty}i^{-2}=\frac{\pi^2}{6}
?i=1
??
??
??i??2
??=?6
?
???2
??
??.
Step by Step Solution
There are 3 Steps involved in it
Step: 1

Get Instant Access to Expert-Tailored Solutions
See step-by-step solutions with expert insights and AI powered tools for academic success
Step: 2

Step: 3

Ace Your Homework with AI
Get the answers you need in no time with our AI-driven, step-by-step assistance
Get Started


