a) Show that for a general M, i.e. not necessarily symmetric, the following equation is also satisfied

(I)

from (II)

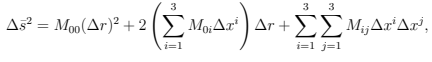b) Since s^2 = 0 in (I) for any {x^i}, replace x^i by x^i in (I) and subtract the equation resulting from (I) to establish that M_0i = 0 for i = 1, 2, 3. c) Use (I) together with s^2 = 0 to set M_ij = (M_00)ij (i, j = 1, 2, 3).

Note: "_" is used to represent subscripts

3 3 3 g? = (r)2 + 2 (, *) r + ; ' , ** 2 (.., ) . 1=1 i=1 j=1 3 3 3 ? = :z3. 9 a=0 =0 3 3 3 g? = (r)2 + 2 (, *) r + ; ' , ** 2 (.., ) . 1=1 i=1 j=1 3 3 3 ? = :z3. 9 a=0 =0