A smartphone manufacturing company operates three factories, each situated in one of three cities: New York, San Francisco, and Los Angeles. These factories supply the manufactured smartphones to three distribution centers located in the city of Chicago. The per-unit transportation cost matrix is provided below:

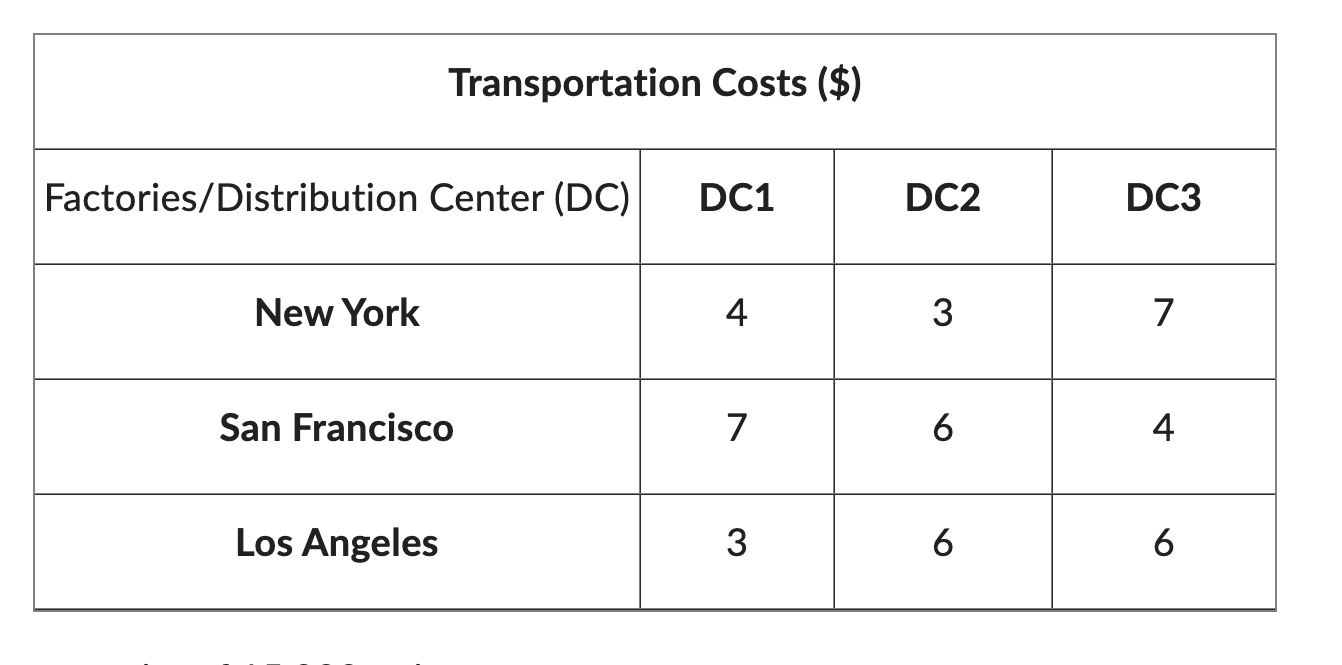
The factory in New York has a capacity of 15,000 units.

The factory in San Francisco has a capacity of 18,000 units.

The factory in Los Angeles has a capacity of 8,000 units.

The requirements of the distribution centers are:

1. Determine how much of the companys production should be shipped from each factory to each distribution center to minimize the total transportation cost.
2. What would be the effect on the optimal solution and the optimal cost if the demand at DC3 increases to 15,000 units?
3. Suppose a new distribution center (DC4) can be used that requires 5,000 units. The transportation cost from New York to DC4 is $4 per unit, from San Francisco to DC4 is $3 per unit, and from Los Angeles to DC4 is $5 per unit. Does using this new distribution center beneficial for the company? Explain from transportation cost and revenue perspectives.

Question 2:

As the manager of a technology department, you have the responsibility to select the most beneficial combination of four software development projects to maximize the department's overall productivity while staying within budget. Each project is represented by a binary decision variable, indicating whether it's chosen (1) or not chosen (0). Additionally, you have constraints on budget and team availability.

The potential benefits (in units of productivity), required team effort (in person-weeks), and associated costs (in thousands of dollars) for each project are as follows:

Project A: Benefit = 30 units, Team Effort = 4 person-weeks, Cost = $10,000

Project B: Benefit = 20 units, Team Effort = 2 person-weeks, Cost = $6,000

Project C: Benefit = 40 units, Team Effort = 5 person-weeks, Cost = $12,000

Project D: Benefit = 25 units, Team Effort = 3 person-weeks, Cost = $8,000

You have a budget constraint of $30,000 and a team availability constraint of 10 person-weeks. Additionally, due to the interdependencies of projects, you cannot select both Project A and Project D simultaneously.

Formulate this as a binary linear optimization problem to find the optimal combination of projects that maximize overall productivity while adhering to the constraints. Please include the decision variables, objective function, and all constraints, and solve the problem using a solver.

PLEASE INCLUDE STEP BY STEP DIRECTIONS FOR CALCULATIONS AND CONSTRAINTS USING THE SOLVER TOOL ON EXCEL

\begin{tabular}{|c|c|c|c|} \hline \multicolumn{4}{|c|}{ Transportation Costs (\$) } \\ \hline Factories/Distribution Center (DC) & DC1 & DC2 & DC3 \\ \hline New York & 4 & 3 & 7 \\ \hline San Francisco & 7 & 6 & 4 \\ \hline Los Angeles & 3 & 6 & 6 \\ \hline \end{tabular} \begin{tabular}{|c|c|} \hline Distribution Centers & Requirement (Smartphones) \\ \hline DC1 & 18,000 \\ \hline DC2 & 12,000 \\ \hline DC3 & 5,000 \\ \hline \end{tabular}