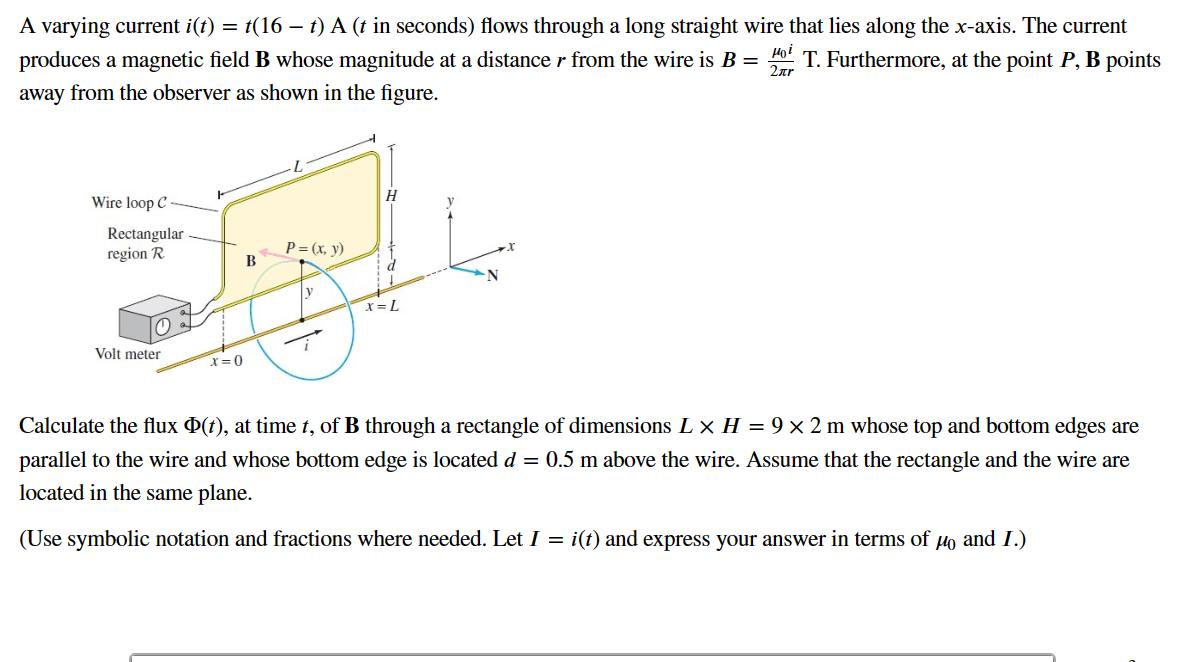
A solid material has thermal conductivity K in kilowatts per meter-kelvin and temperature given at each point by w(x, y, z) = 40 6(x + y + z) C. Use the fact that heat flow is given by the vector field F = -KVw and the rate of heat flow across a surface S within the solid is given by - K ff Vw ds. Find the rate of heat flow out of a sphere of radius 1 (centered at the origin) inside a large cube of copper (K = 400 kW/(m K)). (Use symbolic notation and fractions where needed.) -K Incorrect VU VwdS = 48k kW A varying current i(t) = t(16 t) A (t in seconds) flows through a long straight wire that lies along the x-axis. The current Hoi produces a magnetic field B whose magnitude at a distance r from the wire is B = T. Furthermore, at the point P, B points 2r away from the observer as shown in the figure. Wire loop C Rectangular region R 10 Volt meter x=0 B P = (x, y) y H X=L Calculate the flux (t), at time t, of B through a rectangle of dimensions L x H = 9 x 2 m whose top and bottom edges are parallel to the wire and whose bottom edge is located d = 0.5 m above the wire. Assume that the rectangle and the wire are located in the same plane. (Use symbolic notation and fractions where needed. Let I = i(t) and express your answer in terms of and I.) (Use symbolic notation and fractions where needed. Let I = i(t) and express your answer in terms of and I.) (t) = Use Faraday's Law to determine the voltage drop around the rectangular loop (the boundary of the rectangle) at time t = 7. Assume = 4 . 10-7 T. m/A. (Use symbolic notation and fractions where needed.) /E. T. m E. dr = V Compute f F d.S for the given oriented surface. F = (y, z, x), plane 5x - 6y + z = 1, 0 x 1, 0 y 1, upward-pointing normal Consider the shown work. Tx = = x Ty - dy = d -(x, y, 1 - 5x + 6y) = (1,0,-5) dx -(x, y, 1-5x + 6y) = (0, 1,6) dy Tx x Ty = 1 0 k 5 = 5i - 6j + k = (5, -6, 1) 0 1 6 Because the plane is oriented with upward-pointing normal, the normal vector is N = (5, -6, 1). F((x, y)) = (x, y, 1 - 5x + 6y) F(Q(x, y)) N = (x, y, 1 - 5x + 6y) (5, -6, 1) = 5x - 6y + 1 - 5x + 6y = 1 1 [[ F as = ["'" [" FdS S 1 dx dy Identify the first error in the work shown. . The surface integral is rewritten incorrectly. The surface integral is rewritten incorrectly. F((x, y)) is incorrect. The tangent vectors Tx and T, are incorrect. The normal vector N is incorrect. No errors exist in the work shown. Compute fFdS for the given oriented surface. F = (y, z, x), plane 5x - 6y + z = 1, 0 x 1, 0 y 1, upward-pointing normal (Express numbers in exact form. Use symbolic notation and fractions where needed.) JsFdS =