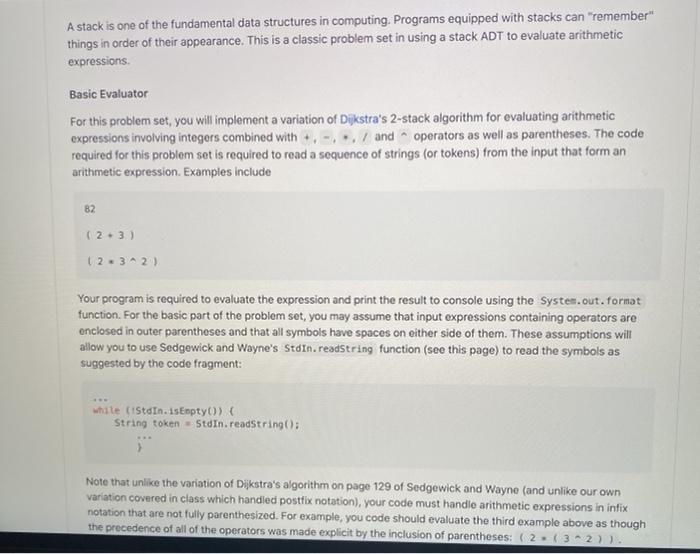
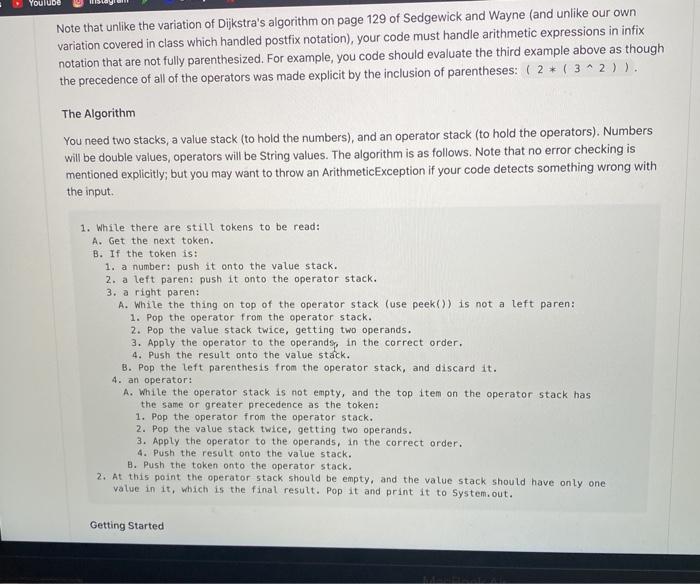
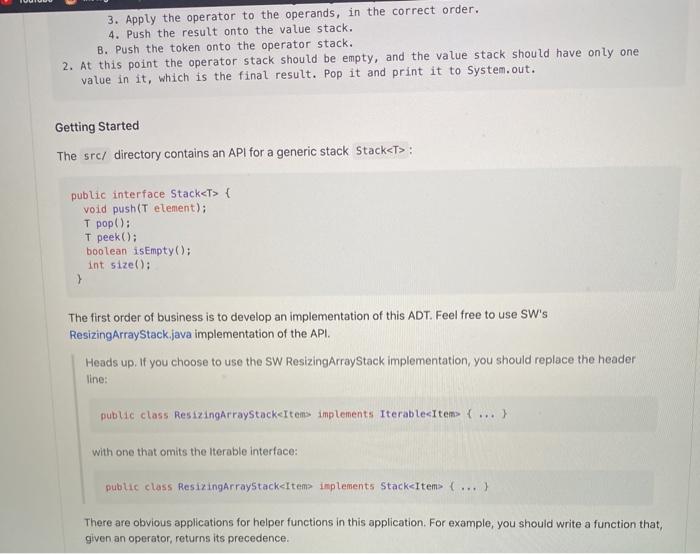
A stack is one of the fundamental data structures in computing. Programs equipped with stacks can "remember" things in order of their appearance. This is a classic problem set in using a stack ADT to evaluate arithmetic expressions Basic Evaluator For this problem set, you will implement a variation of Dijkstra's 2-stack algorithm for evaluating arithmetic expressions involving integers combined with +, -, -, / and operators as well as parentheses. The code required for this problem set is required to read a sequence of strings (or tokens) from the input that form an arithmetic expression. Examples include B2 (23) 123^2) Your program is required to evaluate the expression and print the result to console using the System.out.format function. For the basic part of the problem set, you may assume that input expressions containing operators are enclosed in outer parentheses and that all symbols have spaces on either side of them. These assumptions will allow you to use Sedgewick and Wayne's stdin.readstring function (see this page) to read the symbols as suggested by the code fragment: white (stdin.isEmpty) { String token - Stdin.readString(); Note that unlike the variation of Dijkstra's algorithm on page 129 of Sedgewick and Wayne (and unlike our own variation covered in class which handled postfix notation), your code must handle arithmetic expressions in infix notation that are not fully parenthesized. For example, you code should evaluate the third example above as though the precedence of all of the operators was made explicit by the inclusion of parentheses: (2. (3^2)). Youlude Note that unlike the variation of Dijkstra's algorithm on page 129 of Sedgewick and Wayne (and unlike our own variation covered in class which handled postfix notation), your code must handle arithmetic expressions in infix notation that are not fully parenthesized. For example, you code should evaluate the third example above as though the precedence of all of the operators was made explicit by the inclusion of parentheses: (2* ( 3*2)). The Algorithm You need two stacks, a value stack (to hold the numbers), and an operator stack (to hold the operators). Numbers will be double values, operators will be String values. The algorithm is as follows. Note that no error checking is mentioned explicitly; but you may want to throw an ArithmeticException if your code detects something wrong with the input 1. While there are still tokens to be read: A. Get the next token. B. If the token is: 1. a number: push it onto the value stack. 2. a left paren: push it onto the operator stack. 3. a right paren: A. While the thing on top of the operator stack (use peek()) is not a left paren: 1. Pop the operator from the operator stack. 2. Pop the value stack twice, getting two operands. 3. Apply the operator to the operands, in the correct order. 4. Push the result onto the value stack. B. Pop the left parenthesis from the operator stack, and discard it. 4. an operator: A. While the operator stack is not empty, and the top item on the operator stack has the same or greater precedence as the token: 1. Pop the operator from the operator stack. 2. Pop the value stack twice, getting two operands. 3. Apply the operator to the operands, in the correct order. 4. Push the result onto the value stack. B. Push the token onto the operator stack. 2. At this point the operator stack should be empty, and the value stack should have only one value in it, which is the final result. Pop it and print it to system.out. Getting Started 3. Apply the operator to the operands, in the correct order. 4. Push the result onto the value stack. B. Push the token onto the operator stack. 2. At this point the operator stack should be empty, and the value stack should have only one value in it, which is the final result. Pop it and print it to System.out. Getting Started The src/ directory contains an API for a generic stack Stack : public interface Stack { void push(T element); T pop(); T peek; boolean isEmpty(); int size(): > The first order of business is to develop an implementation of this ADT. Feel free to use SW's ResizingArrayStack.java implementation of the API. Heads up. If you choose to use the SW ResizingArrayStack implementation, you should replace the header line: public class ResizingArraystack ...) with one that omits the Iterable interface: public class ResizingArraystack (...) There are obvious applications for helper functions in this application. For example, you should write a function that, given an operator, returns its precedence