Answered step by step
Verified Expert Solution
Question
1 Approved Answer
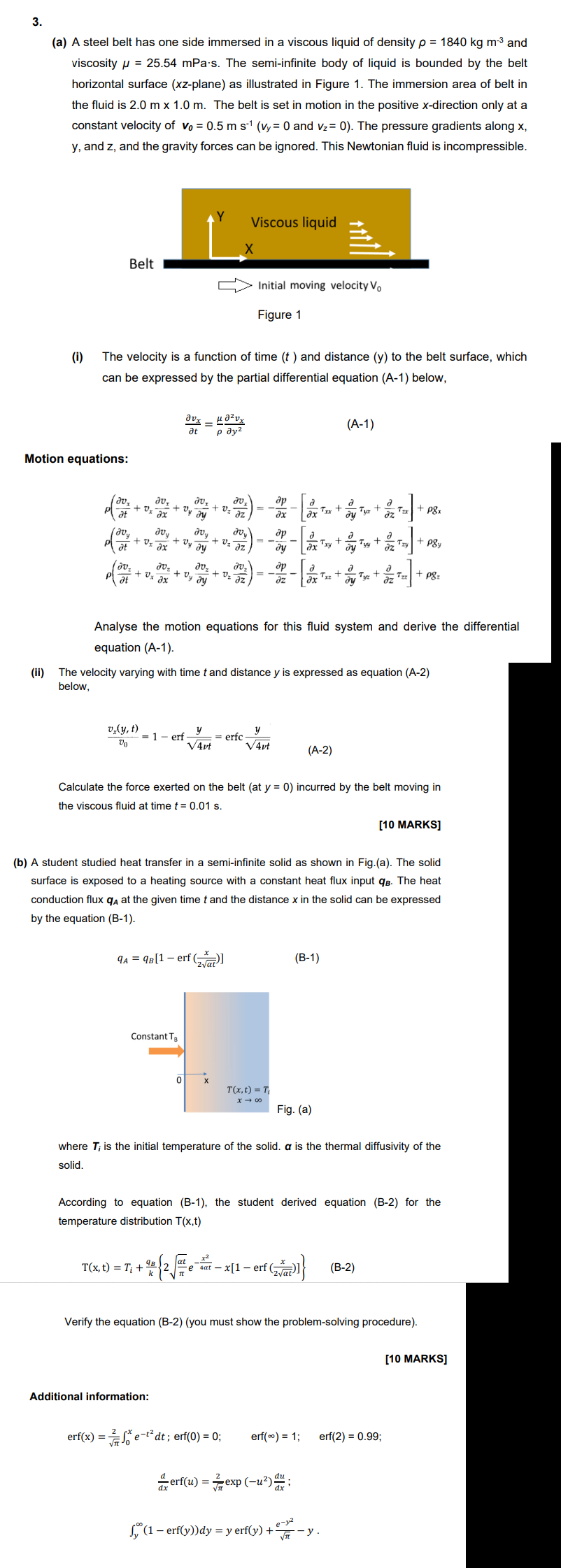
A steel belt has one side immersed in a viscous liquid of density = 1840 kg m-3 and viscosity = 25.54 mPas. The semi-infinite body
A steel belt has one side immersed in a viscous liquid of density = 1840 kg m-3 and viscosity = 25.54 mPas. The semi-infinite body of liquid is bounded by the belt horizontal surface (xz-plane) as illustrated in Figure 1. The immersion area of belt in the fluid is 2.0 m x 1.0 m. The belt is set in motion in the positive x-direction only at a constant velocity of v0 = 0.5 m s-1 (vy = 0 and vz = 0). The pressure gradients along x, y, and z, and the gravity forces can be ignored. This Newtonian fluid is incompressible.
Step by Step Solution
There are 3 Steps involved in it
Step: 1

Get Instant Access to Expert-Tailored Solutions
See step-by-step solutions with expert insights and AI powered tools for academic success
Step: 2

Step: 3

Ace Your Homework with AI
Get the answers you need in no time with our AI-driven, step-by-step assistance
Get Started


