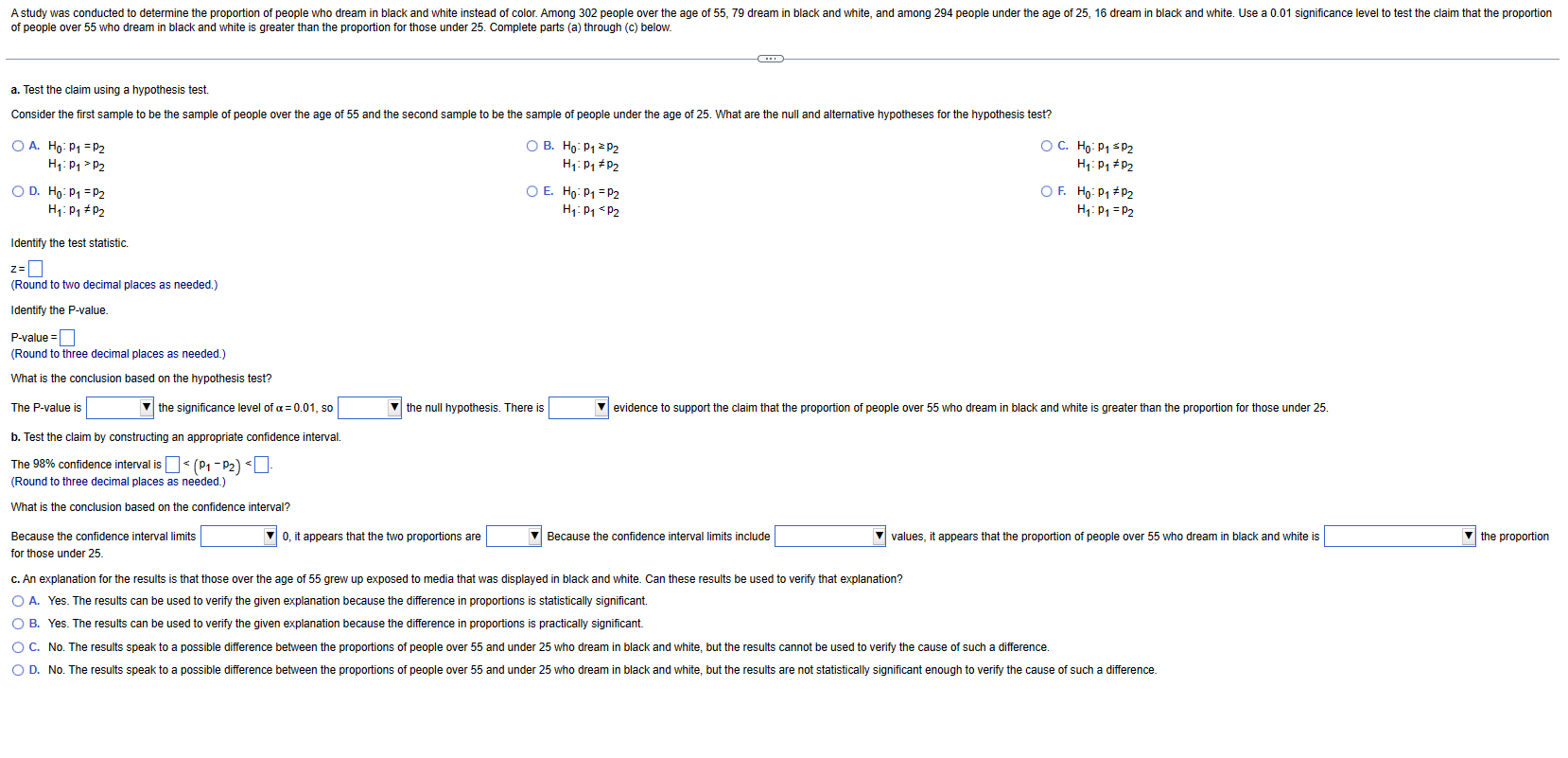
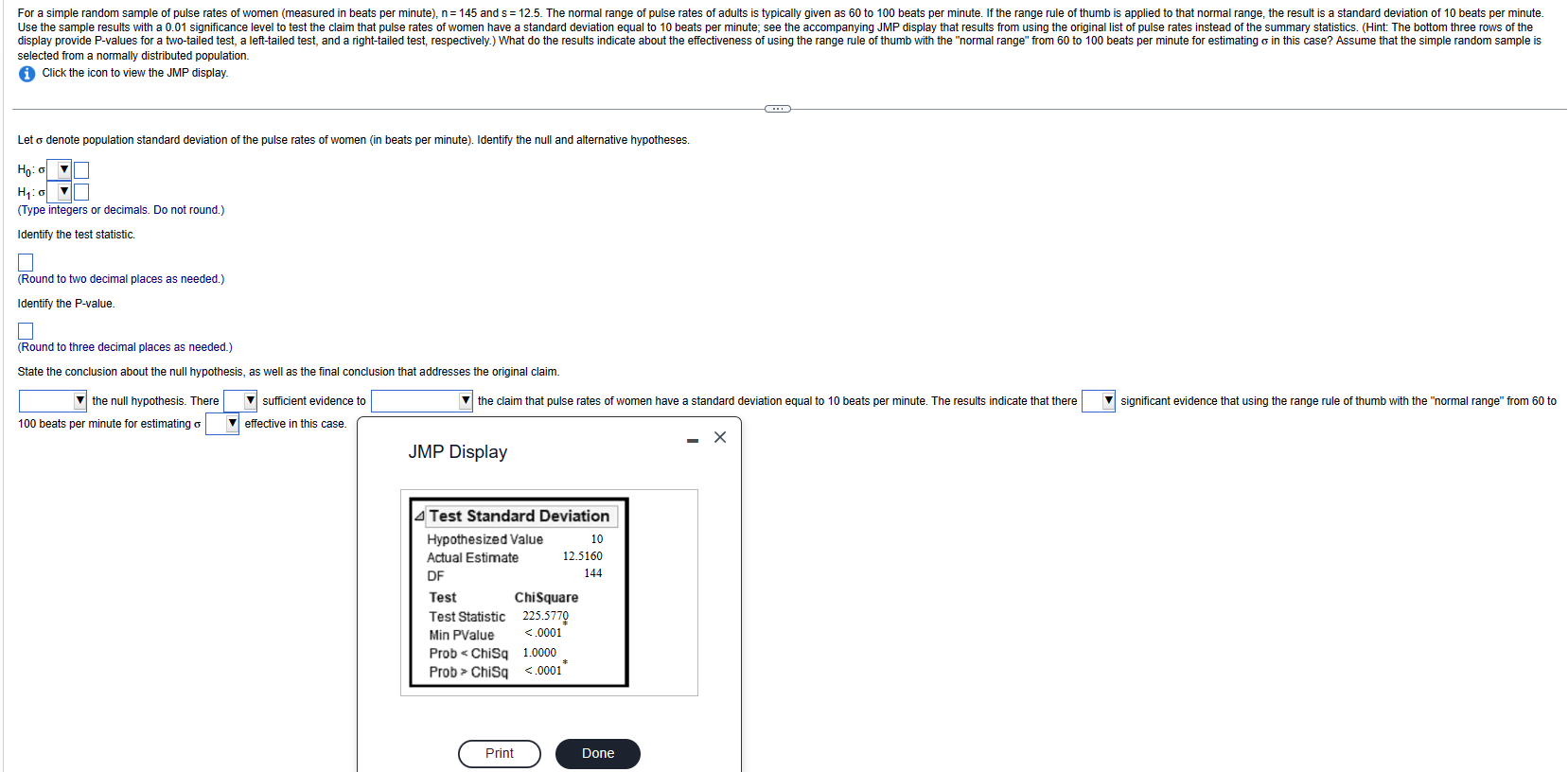
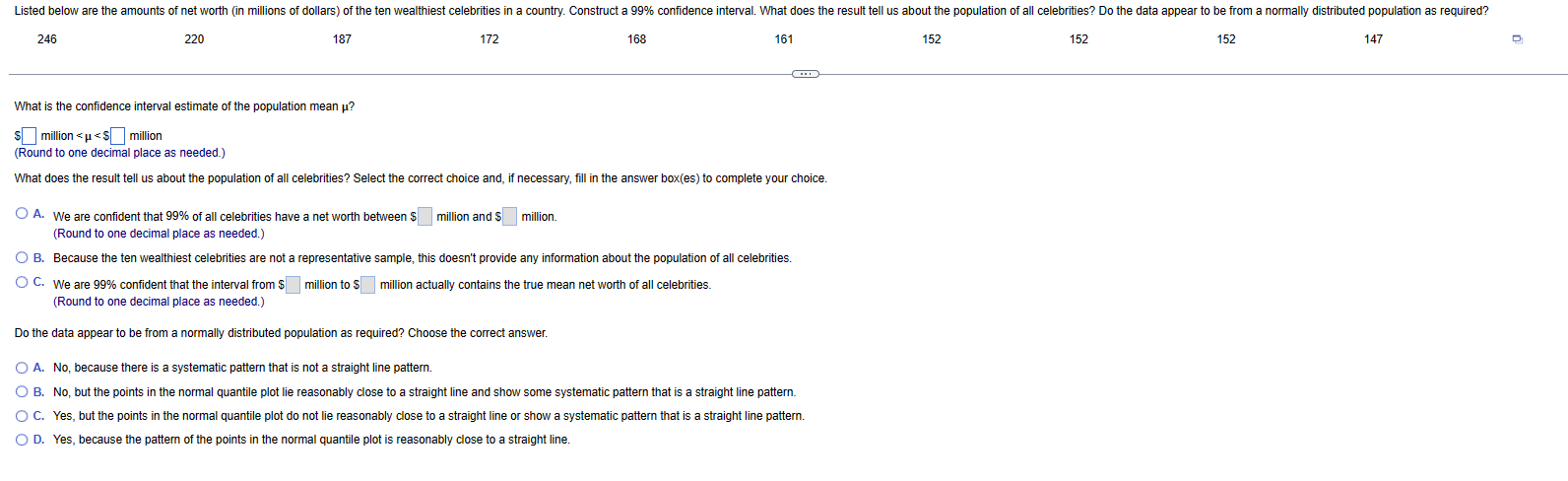
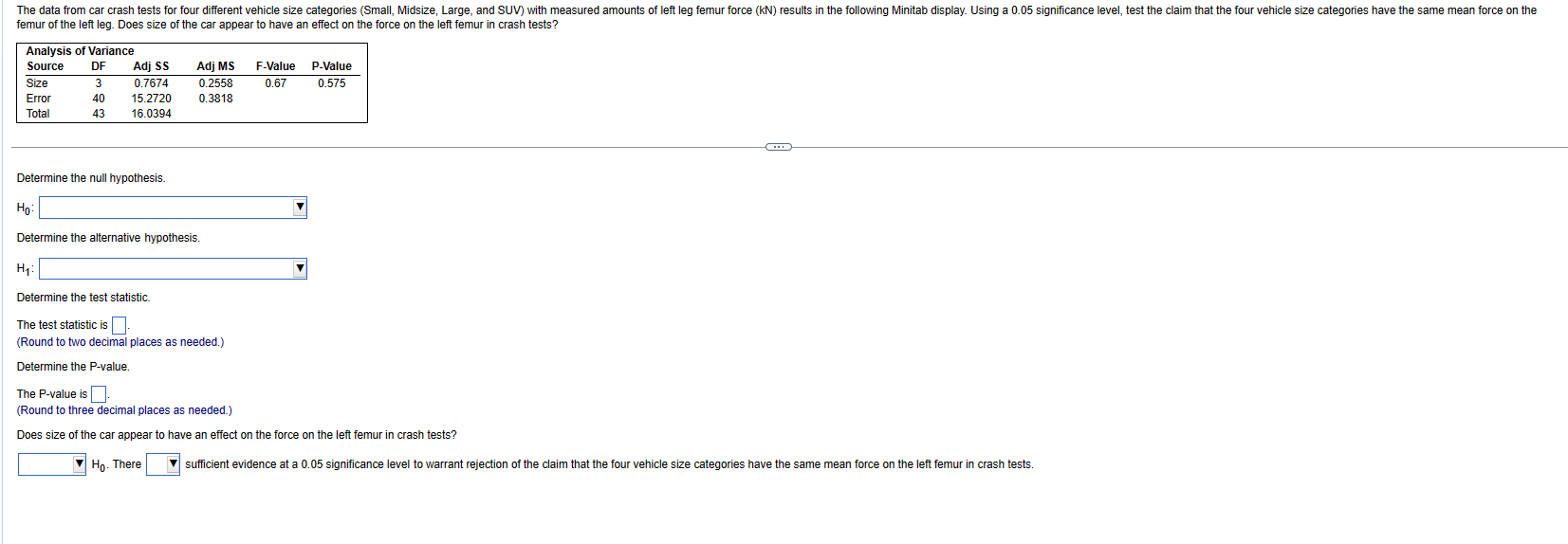
A study was conducted to determine the proportion of people who dream in black and white instead of color. Among 302 people over the age of 55, 79 dream in black and white, and among 294 people under the age of 25, 16 dream in black and white. Use a 0.01 significance level to test the claim that the proportion of people over 55 who dream in black and white is greater than the proportion for those under 25. Complete parts (a) through (c) below. a. Test the claim using a hypothesis test. Consider the first sample to be the sample of people over the age of 55 and the second sample to be the sample of people under the age of 25. What are the null and alternative hypotheses for the hypothesis test? A. Ho: P1=P2 H: P1 P2 OD. Ho: P = P2 H1: P1 P2 Identify the test statistic. z= (Round to two decimal places as needed.) Identify the P-value. P-value (Round to three decimal places as needed.) What is the conclusion based on the hypothesis test? The P-value is B. Ho: P P2 H: P1 P2 E. Ho: P = P2 H: P1 P2 C. Ho: P SP2 H: P1 P2 OF. Ho: P1 P2 H: P1 P2 the significance level of a = 0.01, so the null hypothesis. There is evidence to support the claim that the proportion of people over 55 who dream in black and white is greater than the proportion for those under 25. b. Test the claim by constructing an appropriate confidence interval. The 98% confidence interval is (P1 - P2) For a simple random sample of pulse rates of women (measured in beats per minute), n = 145 and s = 12.5. The normal range of pulse rates of adults is typically given as 60 to 100 beats per minute. If the range rule of thumb is applied to that normal range, the result is a standard deviation of 10 beats per minute. Use the sample results with a 0.01 significance level to test the claim that pulse rates of women have a standard deviation equal to 10 beats per minute; see the accompanying JMP display that results from using the original list of pulse rates instead of the summary statistics. (Hint: The bottom three rows of the display provide P-values for a two-tailed test, a left-tailed test, and a right-tailed test, respectively.) What do the results indicate about the effectiveness of using the range rule of thumb with the "normal range" from 60 to 100 beats per minute for estimating in this case? Assume that the simple random sample is selected from a normally distributed population. Click the icon to view the JMP display. Let o denote population standard deviation of the pulse rates of women (in beats per minute). Identify the null and alternative hypotheses. Hoo H:0 (Type integers or decimals. Do not round.) Identify the test statistic. (Round to two decimal places as needed.) Identify the P-value. (Round to three decimal places as needed.) State the conclusion about the null hypothesis, as well as the final conclusion that addresses the original claim. the null hypothesis. There sufficient evidence to 100 beats per minute for estimating o effective in this case. the claim that pulse rates of women have a standard deviation equal to 10 beats per minute. The results indicate that there significant evidence that using the range rule of thumb with the "normal range" from 60 to JMP Display 4 Test Standard Deviation Hypothesized Value Actual Estimate DF Test 10 12.5160 144 ChiSquare Test Statistic 225.5770 Min PValue A random sample of 740 births in New York State included 363 boys, and that sample is to be used for a test of the common belief that the proportion of male births in the population is equal to 0.512. Complete parts (a) through (c). a. In testing the common belief that the proportion of male babies is equal to 0.512, identify the values of p and p. p= (Round to three decimal places as needed.) 363 b. For random samples of size 740, what sample proportions of male births are at least as extreme as the sample proportion of (Round to three decimal places as needed.) ? Select the correct choice below and fill in the answer box(es) within your choice. 740 OA. Those that are both greater than or equal to OB. Those that are greater than or equal to and less than or equal to OC. Those that are less than or equal to D. Those that are less than or equal to and those that are greater than or equal to c. In using the method of randomization with 1000 resamples, it is found that 251 of them have sample proportions that are at least as extreme as There sufficient evidence to the claim that the proportion of male births is equal to 0.512. 363 740 Using a significance level of 0.05, what should be concluded about the claim that the proportion of male births is equal to 0.512? Listed below are the amounts of net worth (in millions of dollars) of the ten wealthiest celebrities in a country. Construct a 99% confidence interval. What does the result tell us about the population of all celebrities? Do the data appear to be from a normally distributed population as required? 220 246 187 172 168 161 152 152 152 147 What is the confidence interval estimate of the population mean ? $ million Assume that the sample is a simple random sample obtained from a normally distributed population of IQ scores of statistics professors. Use the table below to find the minimum sample size needed to be 95% confident that the sample standard deviation s is within 30% of . Is this sample size practical? To be 95% confident that s is within of the value of 6, the sample size In should be at least 10% 20% 30% 40% 50% 1% 5% 19,205 768 192 48 21 12 8 1% 5% 10% 20% 30% 40% 50% of the value of 6, the sample size In should be at least 33,218 1,336 336 85 38 22 14 To be 99% confident that s is within The minimum sample size needed is Is this sample size practical? A. Yes, because the sample size should be as large as possible for most applications. B. Yes, because the sample size is small enough to be practical for most applications. C. No, because the sample size is excessively large to be practical for most applications. D. No, because the sample size should be as small as possible for most applications. Suppose that in a random selection of 100 colored candies, 30% of them are blue. The candy company claims that the percentage of blue candies is equal to 20%. Use a 0.10 significance level to test that claim. Identify the null and alternative hypotheses for this test. Choose the correct answer below. A. Ho: p = 0.2 H: p>0.2 OB. Ho: p=0.2 H: p 0.2 C. Ho: p 0.2 H: p=0.2 D. Ho: p=0.2 H: p