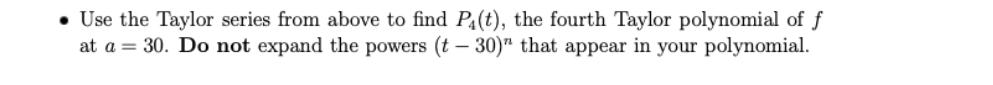
A train runs between two cities every one hour. The amount of time (in minutes) a passenger waits at the train station can be modeled by a normal random variable T with mean 30 and standard deviation = 10. In this problem we will compute the probability that a passenger will wait between 30 and 40 minutes using Taylor series and polynomials. (a) The probability density function of T is f(t) 1 102 -e-(1-0) -00 Use the Taylor series from above to find P4(t), the fourth Taylor polynomial of f at a = 30. Do not expand the powers (t-30)" that appear in your polynomial. (b) Express P(30 T40), the probability that a passenger will wait between 30 and 40 minutes, as an integral of the density function f. Then use P(t) from the previous part to approximate this integral. Show all the steps of your computation and at the end use a calculator to provide a decimal approximation. (c) Now compute the same probability P(30 T40) by converting it to a probability involving the standard normal random variable Z (and referring to the standard normal distribution table). How does this compare to your answer from part (b)?