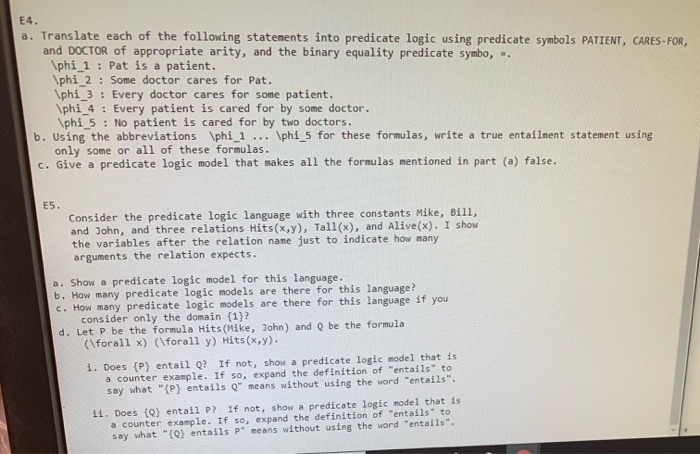
a. Translate each of the following statements into predicate logic using predicate symbols PATIENT, CARES-FOR, and DOCTOR of appropriate arity, and the binary equality predicate symbo, -, \phi_1 : Pat is a patient. \phi_2 : Some doctor cares for Pat. phi 3 : Every doctor cares for some patient. \phi_4 : Every patient is cared for by some doctor. \phi 5 : No patient is cared for by two doctors. b. Using the abbreviations phi 1... \phi 5 for these formulas, write a true entailnent statement using only some or all of these formulas. c. Give a predicate logic model that makes all the formulas mentioned in part (a) false. Consider the predicate logic language with three constants Mike, Bill, and John, and three relations Hits(x,y), Tall(x), and Alive(x). I show the variables after the relation name just to indicate how many arguments the relation expects. a. Show a predicate logic model for this language. b. How many predicate logic models are there for this language? c. How many predicate logic models are there for this language if you consider only the domain {1}? d. Let P be the formula Hits (Mike, John) and be the formula (\forall x) (\forall y) Hits(x,y). i. Does (P} entail Q? If not, show a predicate logic model that is a counter example. If so, expand the definition of "entails" to say what "{P) entails " means without using the word "entails". 11. Does {Q) entail P? If not, show a predicate logic model that is a counter example. If so, expand the definition of "entails" to Say what "{Q} entails p" means without using the word "entails". a. Translate each of the following statements into predicate logic using predicate symbols PATIENT, CARES-FOR, and DOCTOR of appropriate arity, and the binary equality predicate symbo, -, \phi_1 : Pat is a patient. \phi_2 : Some doctor cares for Pat. phi 3 : Every doctor cares for some patient. \phi_4 : Every patient is cared for by some doctor. \phi 5 : No patient is cared for by two doctors. b. Using the abbreviations phi 1... \phi 5 for these formulas, write a true entailnent statement using only some or all of these formulas. c. Give a predicate logic model that makes all the formulas mentioned in part (a) false. Consider the predicate logic language with three constants Mike, Bill, and John, and three relations Hits(x,y), Tall(x), and Alive(x). I show the variables after the relation name just to indicate how many arguments the relation expects. a. Show a predicate logic model for this language. b. How many predicate logic models are there for this language? c. How many predicate logic models are there for this language if you consider only the domain {1}? d. Let P be the formula Hits (Mike, John) and be the formula (\forall x) (\forall y) Hits(x,y). i. Does (P} entail Q? If not, show a predicate logic model that is a counter example. If so, expand the definition of "entails" to say what "{P) entails " means without using the word "entails". 11. Does {Q) entail P? If not, show a predicate logic model that is a counter example. If so, expand the definition of "entails" to Say what "{Q} entails p" means without using the word "entails