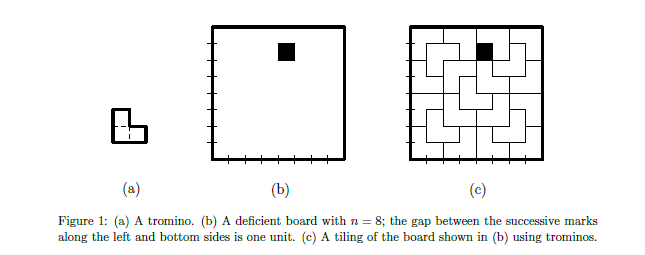
A tromino is an object consists of three 1 x 1 squares that form an L shape; see Figure 1(a) for an an be four different trominos by rotation. An n x n board is called deficient board if exactly one of its 1 x 1 squares is removed; see Figure 1(b) for an example in which n = 8 and the square shown in black is removed. Consider the following problem: given a deficient n x n board, where n is a power of 2, tile the board with trominos. Here, tiling means an exact covering of the board by trominos such that (i) every square of the board except the removed one is covered, (ii) no two trominos overlap each other, and (iii) no tromino extends outside the board. A tiling of the board of Figure 1(b) is shown in Figure 1(c). 1. Design a divide-and-conquer algorithm for the problem. First, explain your algorithm by following the steps of the divide-and-conquer approach, and then write it in pseudocode. 2. Analyze the running time of your algorithm by first stating the recurrence relation form of the time complexity of your algorithm. Then, solving it by one of the methods we learned in class. (b) B (c) Figure 1: (a) A tromino. (b) A deficient board with n=8; the gap between the successive marks along the left and bottom sides is one unit. (c) A tiling of the board shown in (b) using trominos. A tromino is an object consists of three 1 x 1 squares that form an L shape; see Figure 1(a) for an an be four different trominos by rotation. An n x n board is called deficient board if exactly one of its 1 x 1 squares is removed; see Figure 1(b) for an example in which n = 8 and the square shown in black is removed. Consider the following problem: given a deficient n x n board, where n is a power of 2, tile the board with trominos. Here, tiling means an exact covering of the board by trominos such that (i) every square of the board except the removed one is covered, (ii) no two trominos overlap each other, and (iii) no tromino extends outside the board. A tiling of the board of Figure 1(b) is shown in Figure 1(c). 1. Design a divide-and-conquer algorithm for the problem. First, explain your algorithm by following the steps of the divide-and-conquer approach, and then write it in pseudocode. 2. Analyze the running time of your algorithm by first stating the recurrence relation form of the time complexity of your algorithm. Then, solving it by one of the methods we learned in class. (b) B (c) Figure 1: (a) A tromino. (b) A deficient board with n=8; the gap between the successive marks along the left and bottom sides is one unit. (c) A tiling of the board shown in (b) using trominos