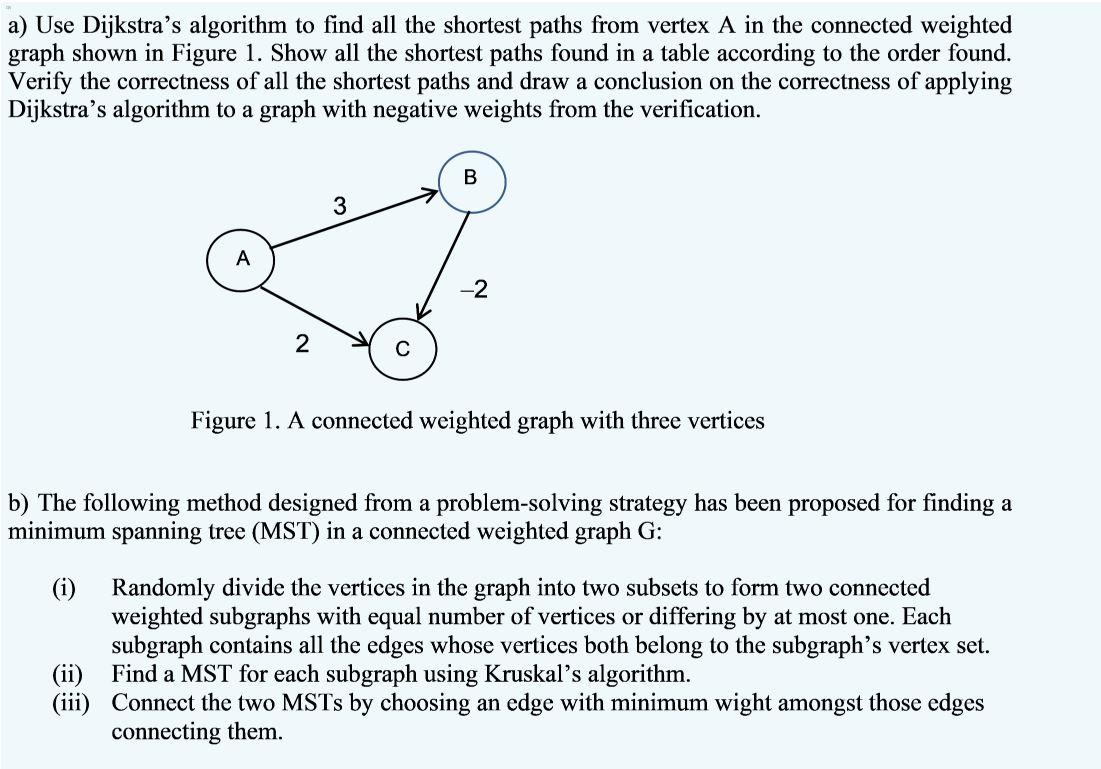
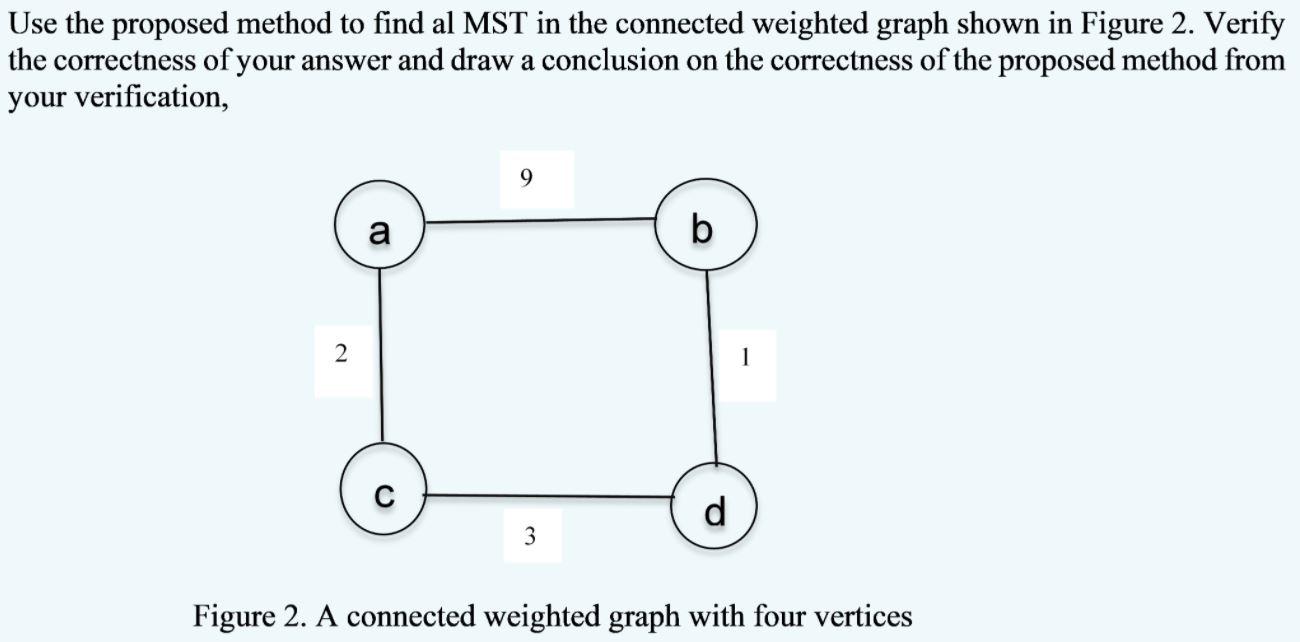
a) Use Dijkstra's algorithm to find all the shortest paths from vertex A in the connected weighted graph shown in Figure 1. Show all the shortest paths found in a table according to the order found. Verify the correctness of all the shortest paths and draw a conclusion on the correctness of applying Dijkstra's algorithm to a graph with negative weights from the verification. B 3 A -2 2 Figure 1. A connected weighted graph with three vertices b) The following method designed from a problem-solving strategy has been proposed for finding a minimum spanning tree (MST) in a connected weighted graph G: (i) Randomly divide the vertices in the graph into two subsets to form two connected weighted subgraphs with equal number of vertices or differing by at most one. Each subgraph contains all the edges whose vertices both belong to the subgraph's vertex set. (ii) Find a MST for each subgraph using Kruskal's algorithm. (iii) Connect the two MSTs by choosing an edge with minimum wight amongst those edges connecting them. Use the proposed method to find al MST in the connected weighted graph shown in Figure 2. Verify the correctness of your answer and draw a conclusion on the correctness of the proposed method from your verification, 9 a b 2 1 d 3 Figure 2. A connected weighted graph with four vertices a) Use Dijkstra's algorithm to find all the shortest paths from vertex A in the connected weighted graph shown in Figure 1. Show all the shortest paths found in a table according to the order found. Verify the correctness of all the shortest paths and draw a conclusion on the correctness of applying Dijkstra's algorithm to a graph with negative weights from the verification. B 3 A -2 2 Figure 1. A connected weighted graph with three vertices b) The following method designed from a problem-solving strategy has been proposed for finding a minimum spanning tree (MST) in a connected weighted graph G: (i) Randomly divide the vertices in the graph into two subsets to form two connected weighted subgraphs with equal number of vertices or differing by at most one. Each subgraph contains all the edges whose vertices both belong to the subgraph's vertex set. (ii) Find a MST for each subgraph using Kruskal's algorithm. (iii) Connect the two MSTs by choosing an edge with minimum wight amongst those edges connecting them. Use the proposed method to find al MST in the connected weighted graph shown in Figure 2. Verify the correctness of your answer and draw a conclusion on the correctness of the proposed method from your verification, 9 a b 2 1 d 3 Figure 2. A connected weighted graph with four vertices








