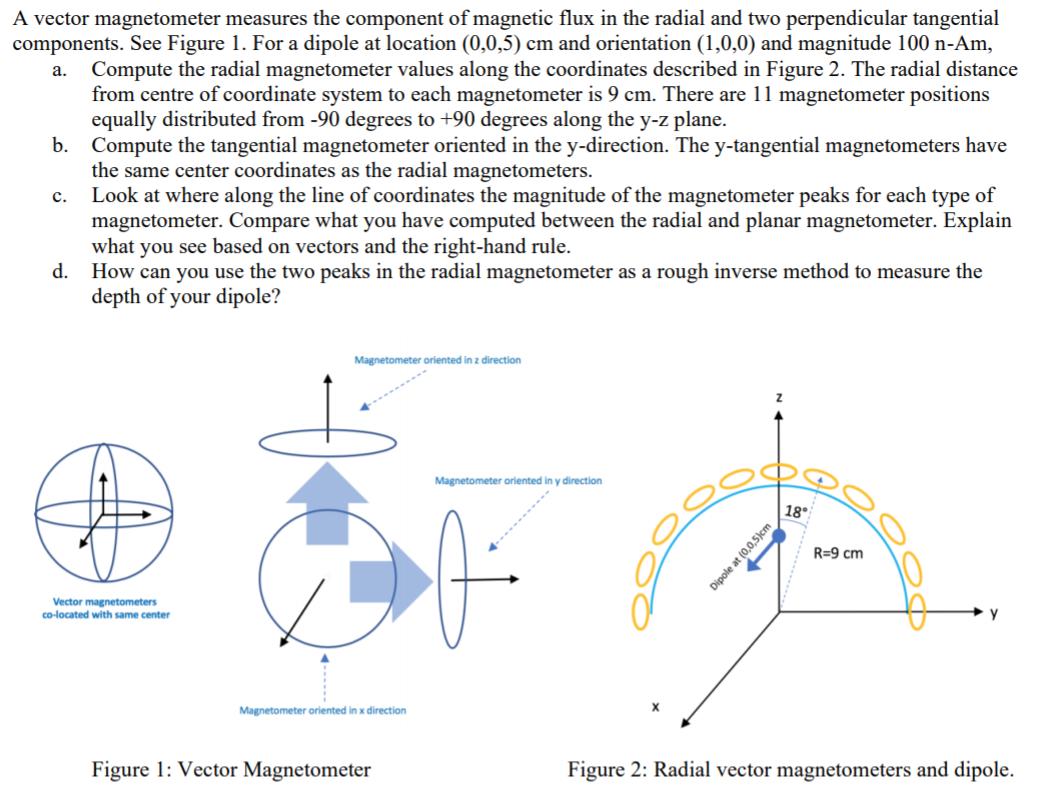
A vector magnetometer measures the component of magnetic flux in the radial and two perpendicular tangential components. See Figure 1. For a dipole at location (0,0,5) cm and orientation (1,0,0) and magnitude 100 n-Am, Compute the radial magnetometer values along the coordinates described in Figure 2. The radial distance from centre of coordinate system to each magnetometer is 9 cm. There are 11 magnetometer positions equally distributed from -90 degrees to +90 degrees along the y-z plane. Compute the tangential magnetometer oriented in the y-direction. The y-tangential magnetometers have the same center coordinates as the radial magnetometers. Look at where along the line of coordinates the magnitude of the magnetometer peaks for each type of magnetometer. Compare what you have computed between the radial and planar magnetometer. Explain what you see based on vectors and the right-hand rule. d. How can you use the two peaks in the radial magnetometer as a rough inverse method to measure the depth of your dipole? . b. . Magnetometer oriented in z direction Magnetometer oriented in y direction 18* R=9 cm Dipole at (0,0,5) Vector magnetometers co-located with same center Magnetometer oriented in x direction Figure 1: Vector Magnetometer Figure 2: Radial vector magnetometers and dipole.