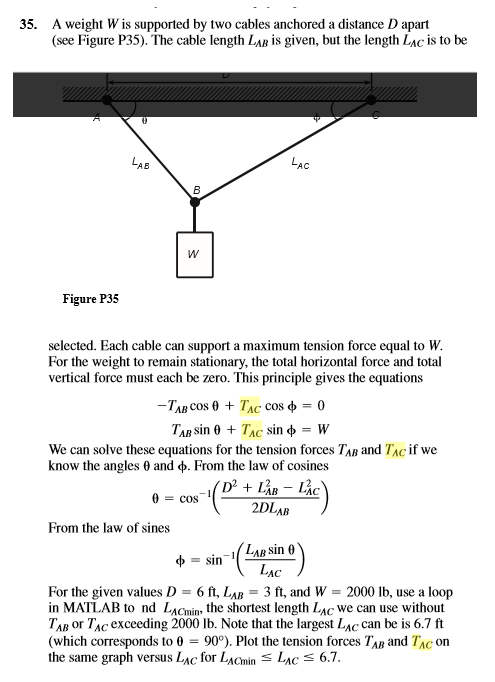
A weight W is supported by two cables anchored a distance D apart (see Figure P35). The cable length L_AB is given, but the length L_AC is to be selected. Each cable can support a maximum tension force equal to W. For the weight to remain stationary, the total horizontal force and total vertical force must each be zero. This principle gives the equations -T_AB cos theta + T_AC cos phi = 0 T_AB sin theta + T_AC sin phi = W We can solve these equations for the tension forces T_AB and T_AC if we know the angles theta and phi. From the law of cosines theta = cos^-1 (D^2 +L^2_AB - L^2_AC/2DL_AB) From the law of sines phi = sin^-1(L_AB sin theta/L_AC) For the given values D = 6 ft, L_AB = 3 ft, and W = 2000 lb, use a loop in MATLAB to and L_ACmin, the shortest length L_AC we can use without T_AB or T_AC exceeding 2000 lb. Note that the largest L_AC can be is 6.7 ft (which corresponds to theta = 90 degree). Plot the tension forces T_AB and T_AC on the same graph versus L_AC for L_ACmin lessthanorequalto L_AC lessthanorequalto 6.7. A weight W is supported by two cables anchored a distance D apart (see Figure P35). The cable length L_AB is given, but the length L_AC is to be selected. Each cable can support a maximum tension force equal to W. For the weight to remain stationary, the total horizontal force and total vertical force must each be zero. This principle gives the equations -T_AB cos theta + T_AC cos phi = 0 T_AB sin theta + T_AC sin phi = W We can solve these equations for the tension forces T_AB and T_AC if we know the angles theta and phi. From the law of cosines theta = cos^-1 (D^2 +L^2_AB - L^2_AC/2DL_AB) From the law of sines phi = sin^-1(L_AB sin theta/L_AC) For the given values D = 6 ft, L_AB = 3 ft, and W = 2000 lb, use a loop in MATLAB to and L_ACmin, the shortest length L_AC we can use without T_AB or T_AC exceeding 2000 lb. Note that the largest L_AC can be is 6.7 ft (which corresponds to theta = 90 degree). Plot the tension forces T_AB and T_AC on the same graph versus L_AC for L_ACmin lessthanorequalto L_AC lessthanorequalto 6.7