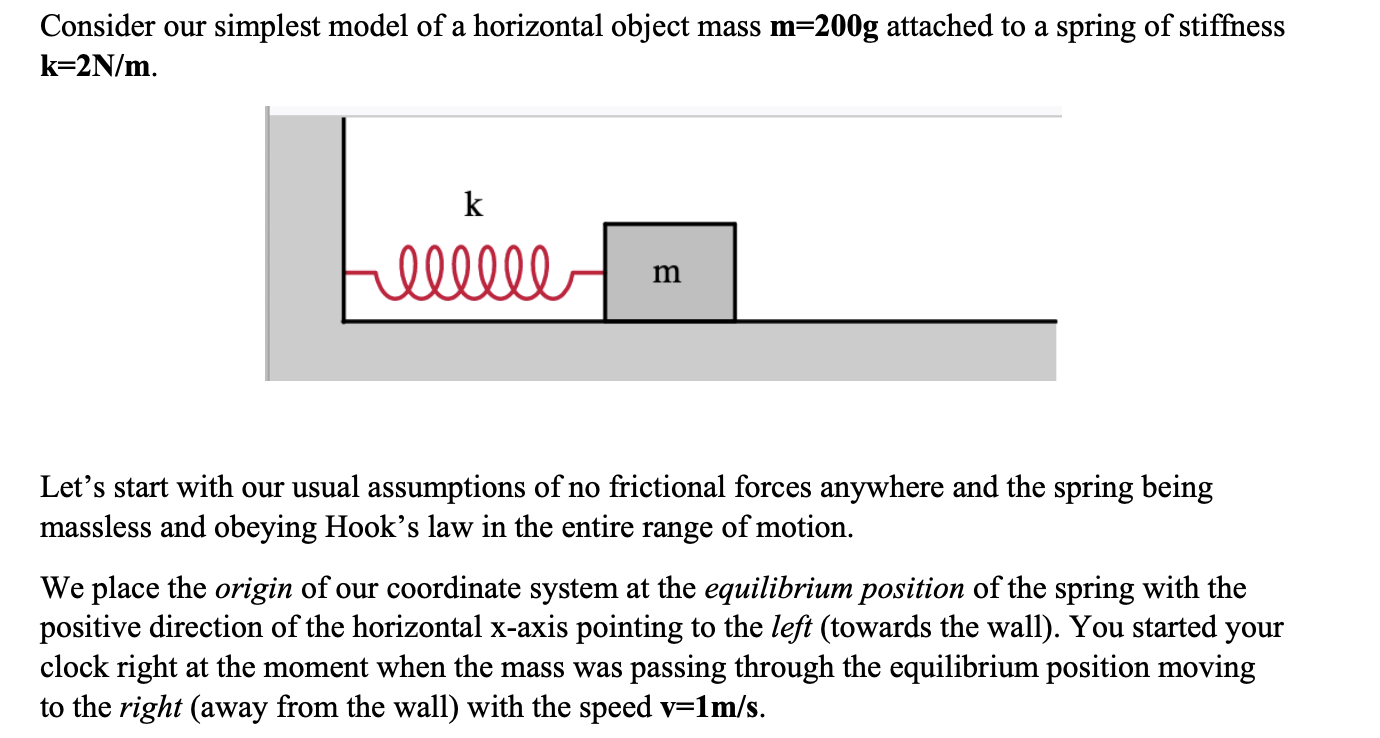
Question
A. Write down an algebraic expression and make a correct graph (not just a sketch) for the velocity of your mass as function of time.
A. Write down an algebraic expression and make a correct graph (not just a sketch) for the velocity of your mass as function of time. Attach the graph with your answer. Explain and show the intermediate steps of how you arrived at your answer. HINT: This is a multistep process which will require you to figure out what trigonometric function best describes the situation, figuring out its correct argument, phase, and amplitude. B. Write down an algebraic expression and make a correct graph (not just a sketch) for the position of your mass as function of time. Attach the graph with your answer. Explain and show the intermediate steps of how you arrived at your answer. HINT: There are many ways to approach this part. You can use your velocity vs. time graph as a starting point to figure out the correct trigonometric function for your position. For the amplitude of your function, you can either use dimensional analysis or conservation of energy. C. Write down an algebraic expression and make a correct graph (not just a sketch) for the acceleration of your mass as function of time. Attach the graph with your answer. Explain and show the intermediate steps of how you arrived at your answer. HINT: There are many ways to approach this part. You can use either your velocity or position vs. time graph as a starting point to figure out the correct trigonometric function for your acceleration. For the amplitude of your function, you can either use dimensional analysis or Newton's laws. D. Write down an algebraic expression and make a correct graph (not just a sketch) for the kinetic energy of your mass as function of time. Attach the graph with your answer. Explain and show the intermediate steps of how you arrived at your answer. E. Write down an algebraic expression and make a correct graph (not just a sketch) for the potential energy of your mass as function of time. Attach the graph with your answer. Explain and show the intermediate steps of how you arrived at your answer. F. The kinetic and potential energy curves oscillate, but not about zero. They also seem to oscillate twice as fast as the velocity or position curves. Is this correct? Explain. G. Write down an algebraic expression and make a correct graph (not just a sketch) for the total energy of your mass as function of time. Attach the graph with your answer. Simplify your answer as much as possible. Explain and show the intermediate steps of how you arrived at your answer. Does your answer seem consistent with the principles of conservation of energy? Explain.
Step by Step Solution
There are 3 Steps involved in it
Step: 1

Get Instant Access to Expert-Tailored Solutions
See step-by-step solutions with expert insights and AI powered tools for academic success
Step: 2

Step: 3

Ace Your Homework with AI
Get the answers you need in no time with our AI-driven, step-by-step assistance
Get Started


