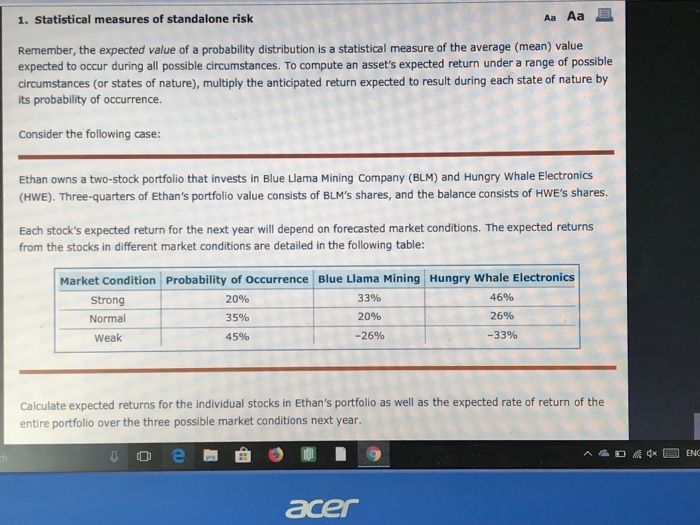
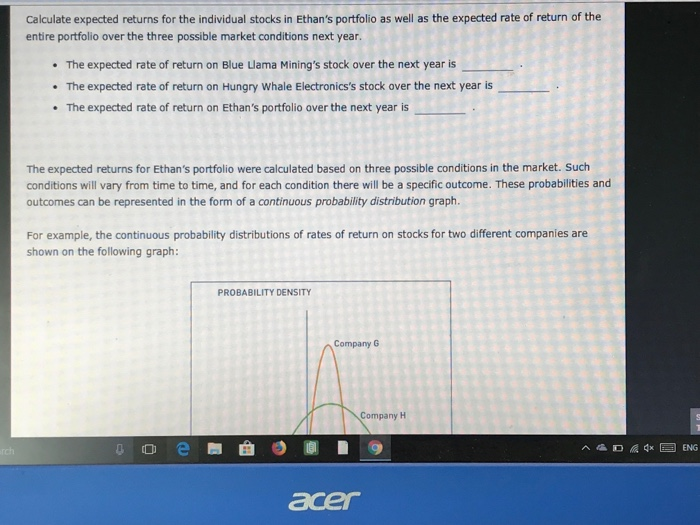
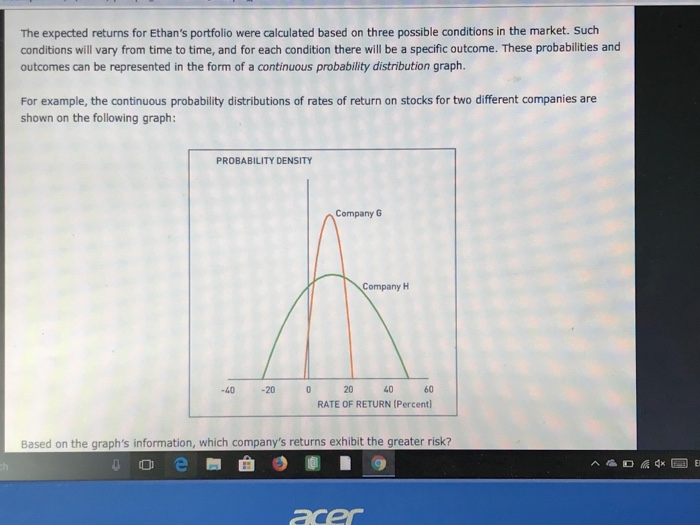
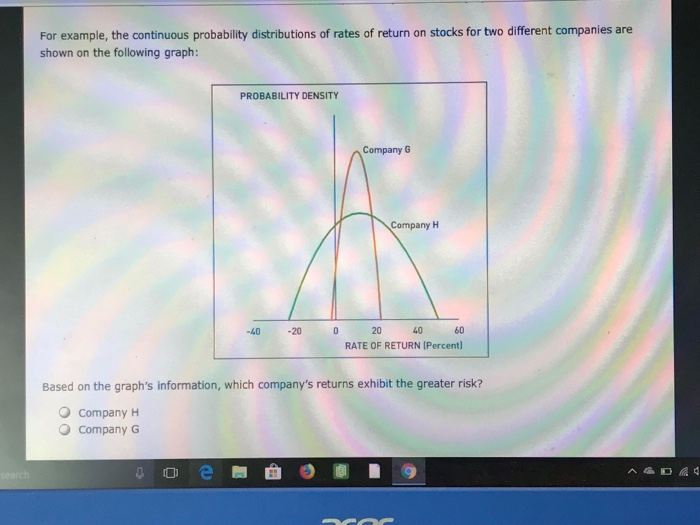
Aa Aa 1. Statistical measures of standalone risk Remember, the expected value of a probability distribution is a statistical measure of the average (mean) value expected to occur during all possible circumstances. To compute an asset's expected return under a range of possible circumstances (or states of nature), multiply the anticipated return expected to result during each state of nature by its probability of occurrence Consider the following case: Ethan owns a two-stock portfolio that invests in Blue Llama Mining Company (BLM) and Hungry Whale Electronics (HWE). Three-quarters of Ethan's portfolio value consists of BLM's shares, and the balance consists of HWE's shares. Each stock's expected return for the next year will depend on forecasted market conditions. The expected returns from the stocks in different market conditions are detailed in the following table: Market Condition Probability of occurrence Blue LIama Mining Hungry Whale Electronics 4690 20% 33% Strong 20% 26% 35% Normal -26% 45% -33% Weak Calculate expected returns for the individual stocks in Ethan's portfolio as well as the expected rate of return of the entire portfolio over the three possible market conditions next year acer Calculate expected returns for the individual stocks in Ethan's portfolio as well as the expected rate of return of the entire portfolio over the three possible market conditions next year. The expected rate of return on Blue Llama Mining's stock over the next year is The expected rate of return on Hungry whale Electronics's stock over the next year is The expected rate of return on Ethan's portfolio over the next year is The expected returns for Ethan's portfolio were calculated based on three possible conditions in the market. Such conditions will vary from time to time, and for each condition there will be a specific outcome. These probabilities and outcomes can be represented in the form of a continuous probability distribution graph. For example, the continuous probability distributions of rates of return on stocks for two different companies are shown on the following graph: PROBABILITY DENSITY Company G Company H acer The expected returns for Ethan's portfolio were calculated based on three possible conditions in the market. Such conditions will vary from time to time, and for each condition there will be a specific outcome. These probabilities and outcomes can be represented in the form of a continuous probability distribution graph. For example, the continuous probability distributions of rates of return on stocks for two different companies are shown on the following graph: PROBABILITY DENSITY Company G Company H -40 -20 0 20 40 60 RATE OF RETURN (Percent Based on the graph's information, which company's returns exhibit the greater risk? For example, the continuous probability distributions of rates of return on stocks for two different companies are shown on the following graph: PROBABILITY DENSITY Company G Company H 20 40 RATE OF RETURN (Percent) -40 -20 60 Based on the graph's information, which company's returns exhibit the greater risk? O Company H Company G