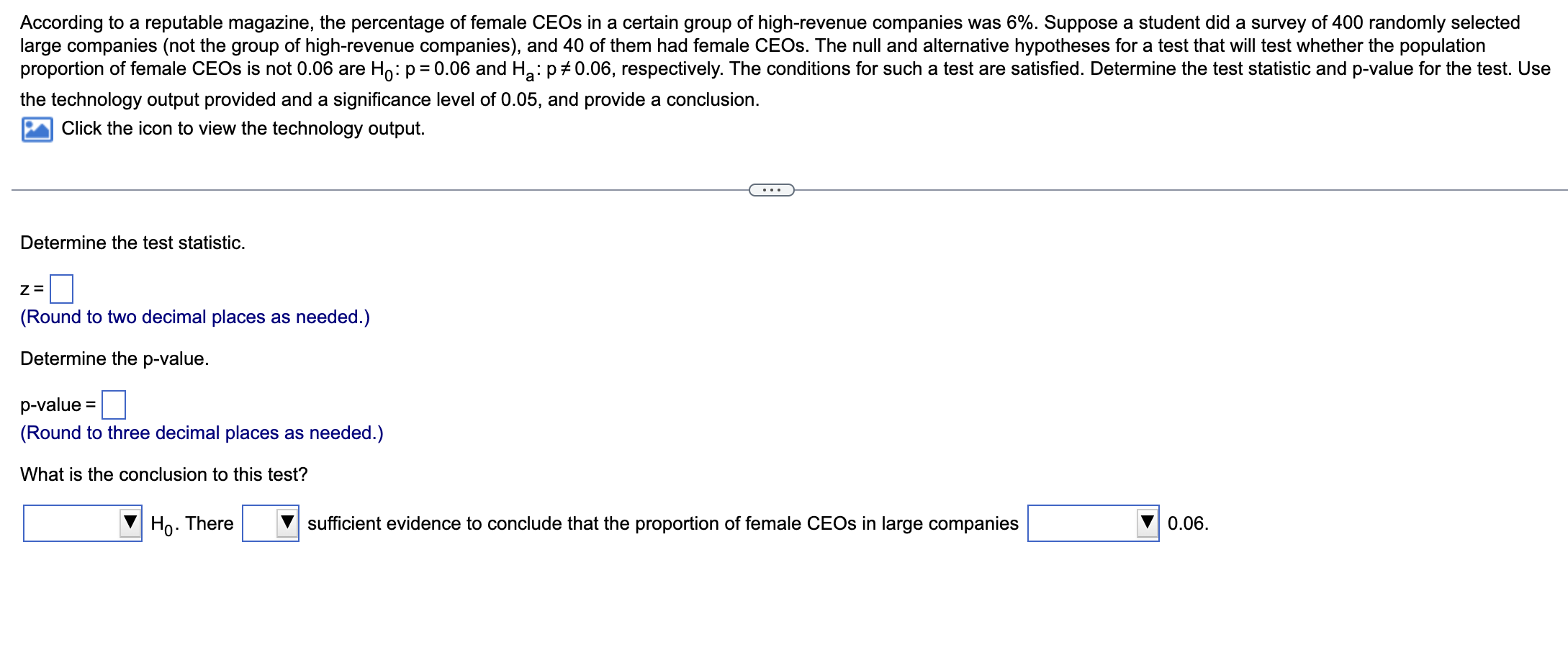
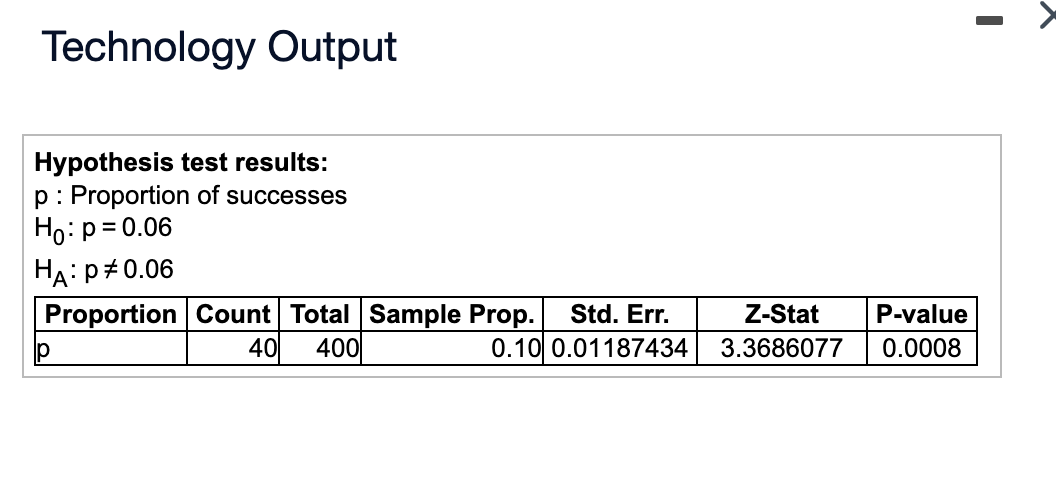
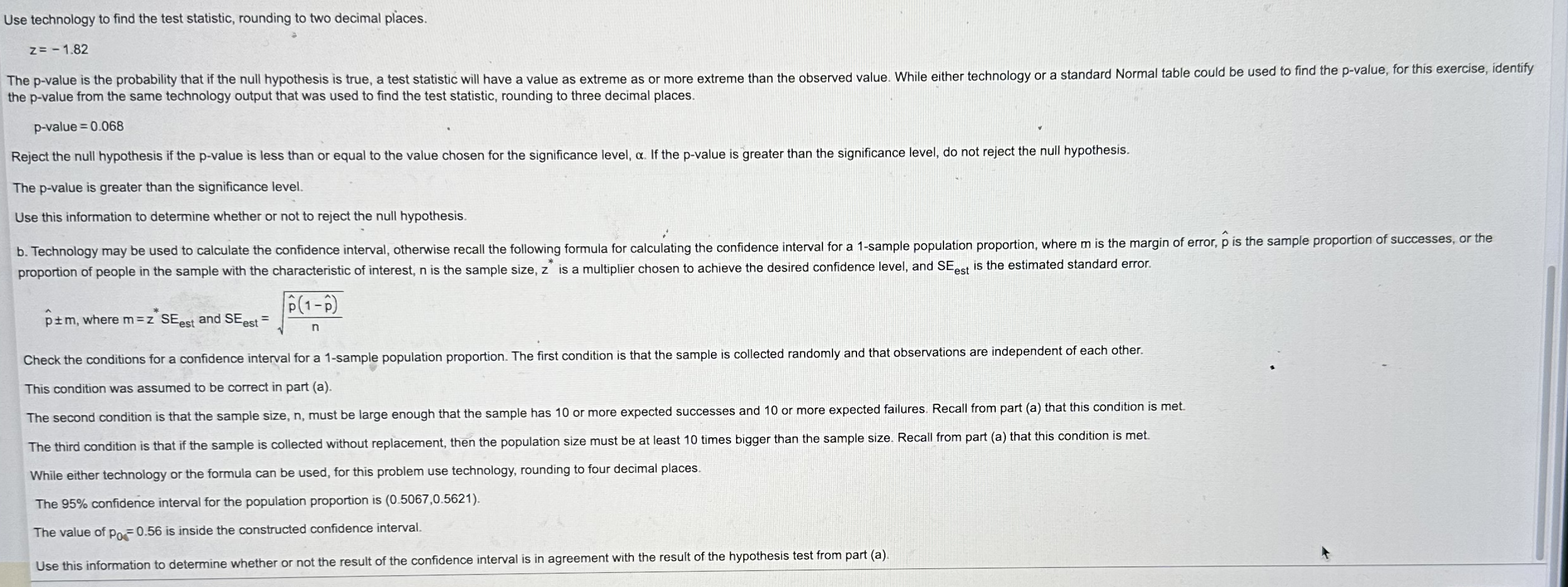
According to a reputable magazine, the percentage of female CEOs in a certain group of high-revenue companies was 6%. Suppose a student did a survey of 400 randomly selected large companies (not the group of high-revenue companies), and 40 of them had female CEOs. The null and alternative hypotheses for a test that will test whether the population proportion of female CEOs is not 0.06 are Ho: p = 0.06 and Ha: p 0.06, respectively. The conditions for such a test are satisfied. Determine the test statistic and p-value for the test. Use the technology output provided and a significance level of 0.05, and provide a conclusion. Click the icon to view the technology output. Determine the test statistic. Z= (Round to two decimal places as needed.) Determine the p-value. p-value = (Round to three decimal places as needed.) What is the conclusion to this test? Ho. There sufficient evidence to conclude that the proportion of female CEOs in large companies 0.06. Technology Output Hypothesis test results: p Proportion of successes Ho p=0.06 HA: P0.06 Proportion Count Total Sample Prop. 40 400 Std. Err. 0.10 0.01187434 Z-Stat P-value 3.3686077 0.0008 A 2018 poll of 2202 randomly selected U.S. adults found that 39.92% planned to watch at least a "fair amount" of a particular sporting event in 2018. In 2014, 48% of U.S. adults reported planning to watch at least a "fair amount." a. Does this sample give evidence that the proportion of U.S. adults who planned to watch the 2018 sporting event was less than the proportion who planned to do so in 2014? Use a 0.05 significance level. b. After conducting the hypothesis test, a further question one might ask is what proportion of all U.S. adults planned to watch at least a "fair amount" of the sporting event in 2018. Use the sample data to construct a 90% confidence interval for the population proportion. How does your confidence interval support your hypothesis test conclusion? a. State the null and alternative hypotheses. Let p be the proportion of U.S. adults that planned to watch at least a "fair amount" of the sporting event. Hop Ha: P (Type integers or decimals. Do not round.) Compute the z-test statistic. z= (Round to two decimal places as needed.) Compute the p-value. p-value = (Round to three decimal places as needed.) Reject Ho or do not reject Ho and interpret the conclusion. Choose the correct answer below. A. Reject Ho. There is sufficient evidence to suggest that the percentage in 2018 is significantly less than 48%. B. Do not reject Ho. There is sufficient evidence to suggest that the percentage in 2018 is significantly less than 48%. C. Do not reject Ho. There is not sufficient evidence to suggest that the percentage in 2018 is significantly different from 48%. D. Reject Ho. There is not sufficient evidence to suggest that the percentage in 2018 is significantly different from 48%. b. The 90% confidence interval for the population proportion is ( , ). (Round to four decimal places as needed.) The result of the 90% confidence interval values less than the value of po with the result of the hypothesis test performed in part (a) because the 90% confidence interval X A 2018 poll of 1250 randomly selected users of a social media site found that 668 get most of their news about world events on the site. Research done in 2013 found that only 56% of all the site users reported getting their news about world events on this site. a. Does this sample give evidence that the proportion of site users who get their world news on this site has changed since 2013? Carry out a hypothesis test and use a 0.05 significance level. b. After conducting the hypothesis test, a further question one.might ask is what proportion of all of the site users get most of their news about world events on the site in 2018. Use the sample data to construct a 95% confidence interval for the population proportion. How does your confidence interval support your hypothesis test conclusion? The null hypothesis is the neutral, status quo, skeptical statement about a population parameter. In the context of researching new ideas, the null hypothesis often represents "no change," "no effect," or "no difference." The alternative hypothesis is the research hypothesis. It is a statement about the value of a parameter that the researcher intends to demonstrate is true. State the null and alternative hypotheses. Let p be the proportion of site users who get their world news on the site. Ho: p=0.56 Ha p 0.56 Choose the one-proportion z-test. This test has several conditions. The Random Sample condition states that the sample must be collected randomly from the population. The Large Sample Size condition states that the sample size, n, must be large enough that the sample has 10 or more expected successes and 10 or more expected failures; in other words, npo 10 and n(1-po) 10. The Large Population condition states that if the sample is collected without replacement, then the population size must be at least 10 times bigger than the sample size. If the sample is drawn without replacement, then any size population will work. The Independence condition states that each observation or measurement must have no influence on any others. First, check that the sample is random and independent. It is given that the sample is a random sample, and it is reasonable to assume that respondents in a random sample are independent. Next, check the expected number of successes and failures. Recall that the hypothesized population proportion is po = 0.56. Identify the sample size. n = 1250 Determine the expected number of successes and failures, rounding to the nearest whole number. npo 1250 x 0.56 700 n(1-Po) = 1250(1-0.56) = 550 There are at least 10 or more expected successes and 10 or more expected failures, so this condition is met. If the sample is collected without replacement, then the population size must be at least 10 times bigger than the sample size. It is reasonable to assume that this condition is met, since the social media site can be assumed to have more than 12,500 users. Thus, all of the conditions for the one-proportion z-test are satisfied. Now choose the significance level. The significance level is = 0.05. P-Po Po (1-Po) The formula for the z-test statistic is where SE= SE n p is the sample proportion, po is the hypothesized proportion, and n is the sample size. While either technology or the formula could be used to find the test statistic, for this exercise, use technology. Identify the number of successes. Use technology to find the test statistic, rounding to two decimal places. z=-1.82 The p-value is the probability that if the null hypothesis is true, a test statistic will have a value as extreme as or more extreme than the observed value. While either technology or a standard Normal table could be used to find the p-value, for this exercise, identify the p-value from the same technology output that was used to find the test statistic, rounding to three decimal places. p-value=0.068 Reject the null hypothesis if the p-value is less than or equal to the value chosen for the significance level, a. If the p-value is greater than the significance level, do not reject the null hypothesis. The p-value is greater than the significance level. Use this information to determine whether or not to reject the null hypothesis. b. Technology may be used to calculate the confidence interval, otherwise recall the following formula for calculating the confidence interval for a 1-sample population proportion, where m is the margin of error, p is the sample proportion of successes, or the proportion of people in the sample with the characteristic of interest, n is the sample size, z is a multiplier chosen to achieve the desired confidence level, and SE est is the estimated standard error. pm, where m=z SE est and SE est= (1-p) n Check the conditions for a confidence interval for a 1-sample population proportion. The first condition is that the sample is collected randomly and that observations are independent of each other. This condition was assumed to be correct in part (a). The second condition is that the sample size, n, must be large enough that the sample has 10 or more expected successes and 10 or more expected failures. Recall from part (a) that this condition is met. The third condition is that if the sample is collected without replacement, then the population size must be at least 10 times bigger than the sample size. Recall from part (a) that this condition is met. While either technology or the formula can be used, for this problem use technology, rounding to four decimal places. The 95% confidence interval for the population proportion is (0.5067,0.5621). The value of Po0.56 is inside the constructed confidence interval. Use this information to determine whether or not the result of the confidence interval is in agreement with the result of the hypothesis test from part (a).