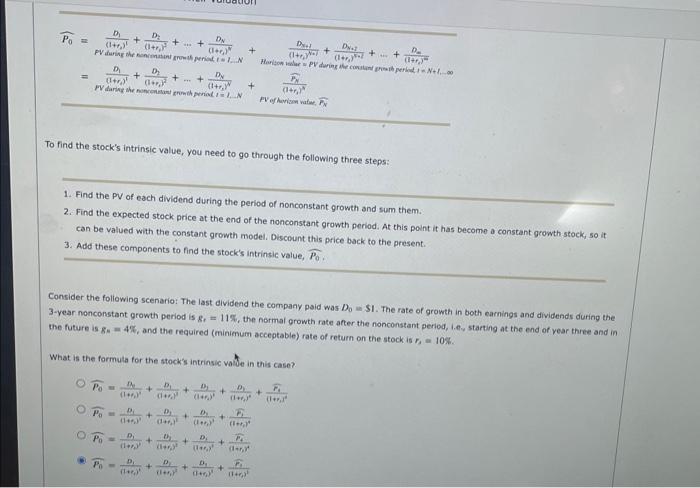
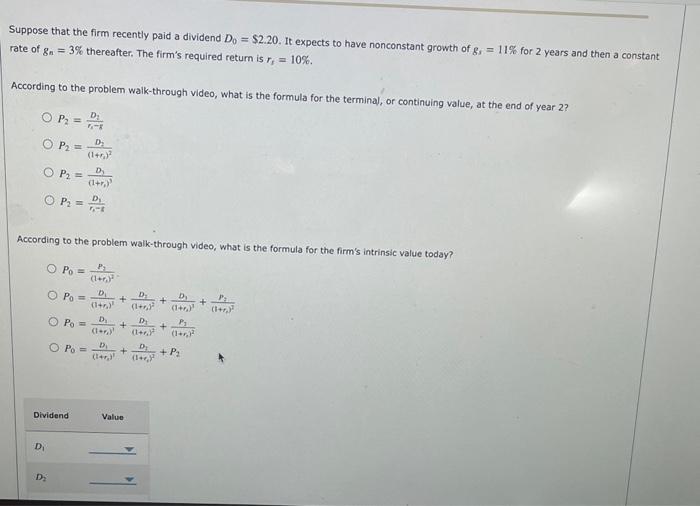
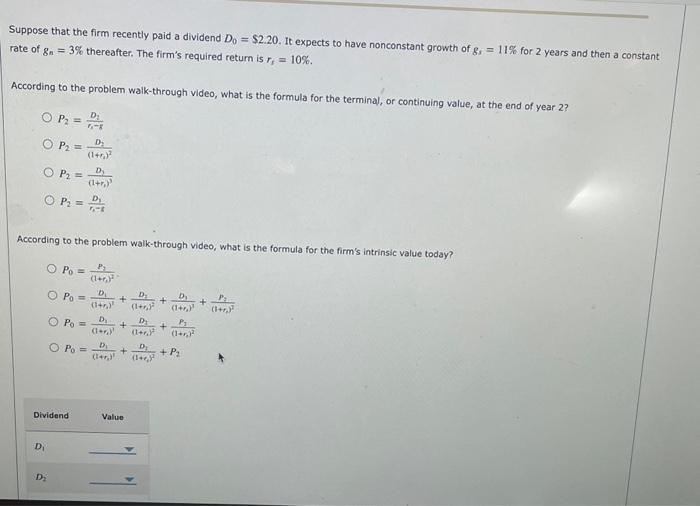
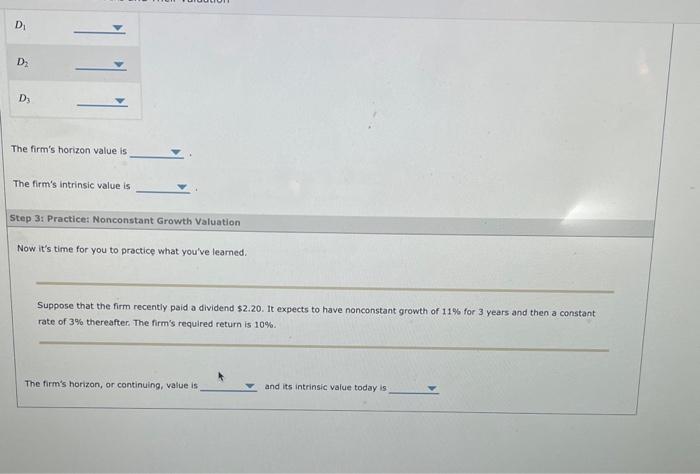
Accurate estimates of future dividends are not easily available. For some companies it is reasonable to assume that dividends will grow at a constant rate. However, most firms go through life cycles where they experience different growth rates during different parts of the cycle. In their early years, most firms grow much faster than the economy as a whole; then they match the economy's growth; and finally they grow at a slower rate than the economy. These firms are called supernormal, or nonconstant, growth firms. The value of this firm's stock, like any other asset, is the present value of its expected future dividends as determined by Value of stock, P0=PV of expected future dividends =(1+r1)tD1+(1+E1)1D1++(1+r1)2D2=1=1(1++yyD1 When D1 is growing at a constant rate, you can simplify the previous equation as follows: P0=f11D1 In the supernormal case, however, the expected growth rate is not a constant, seil, you can combine both equations to construct a new formula for valuing the stock. First, assuming that a company currently enjoying supernormat growth will slow down in N periods ( N is often called the horizon, or terminal, date) and then will grow at a constant rate, g. Second, you can use the constant growth formula to determine what the stock's horizon value will be N periods from totay: Horizon walue, PN=h1rDm=1. Pverharian vatwe, FN To find the stock's intrinsic value, you need to go through the following three steps: 1. Find the PV of each dividend during the period of nonconstant growth and sum them. 2. Find the expected stock price at the end of the nonconstant growth period. At this point it has become a constant gcowth stock, so it can be valued with the constant growth model. Discount this price back to the present. 3. Add these components to find the stock's intrinsic value, P0. 3-year nonconstant growth period is grr=11%, the normal growth rate after the fionconstant period, l.t.y startifg at the end of year three and in the future is ge=4%, and the required (minienum acceptable) rate of return on the stock is ra=10%. What is the formuta for the stock's intrinsic volide in this case? Pverharian vatwe, FN To find the stock's intrinsic value, you need to go through the following three steps: 1. Find the PV of each dividend during the period of nonconstant growth and sum them. 2. Find the expected stock price at the end of the nonconstant growth period. At this point it has become a constant gcowth stock, so it can be valued with the constant growth model. Discount this price back to the present. 3. Add these components to find the stock's intrinsic value, P0. 3-year nonconstant growth period is grr=11%, the normal growth rate after the fionconstant period, l.t.y startifg at the end of year three and in the future is ge=4%, and the required (minienum acceptable) rate of return on the stock is ra=10%. What is the formuta for the stock's intrinsic volide in this case? Suppose that the firm recently paid a dividend D0=$2.20. It expects to have nonconstant growth of gs=11% for 2 years and then a constant rate of gn=3% thereafter. The firm's required return is rs=10%. According to the problem walk-through video, what is the formula for the terminal, or continuing value, at the end of year 2 ? P2=r1rD2P2=(1+r1)2D2P2=(1+r1)3D2P2=r1tD1 According to the problem walk-through video, what is the formula for the firm's intrinsic value today? P0=(1+t1)2P2P0=(1+r2)2D1+(1+r2)2D2+(1+r2)2D1+(1+r1)2P2P0=(1+r1)2D1+(1+r1)2D1+(1+r0)2P1P0=(1+r2)2D1+(1++1)2D1+P2 Suppose that the firm recently paid a dividend D0=$2.20. It expects to have nonconstant growth of gs=11% for 2 years and then a constant rate of gn=3% thereafter. The firm's required return is rs=10%. According to the problem walk-through video, what is the formula for the terminal, or continuing value, at the end of year 2 ? P2=r1rD2P2=(1+r1)2D2P2=(1+r1)3D2P2=r1tD1 According to the problem walk-through video, what is the formula for the firm's intrinsic value today? P0=(1+t1)2P2P0=(1+r2)2D1+(1+r2)2D2+(1+r2)2D1+(1+r1)2P2P0=(1+r1)2D1+(1+r1)2D1+(1+r0)2P1P0=(1+r2)2D1+(1++1)2D1+P2 The firm's horizon value is The firm's intrinsic value is Step 3: Practice: Nonconstant Growth Valuation Now it's time for you to practice what you've leamed. Suppose that the firm recently paid a dividend $2.20. It expects to have nonconstant growth of 11% for 3 years and then a constant rate of 3% thereafter. The firm's required return is 10%. The firm's horizon, or continuing, value is and its intrinsic value today is The firm's horizon value is The firm's intrinsic value is Step 3: Practice: Nonconstant Growth Valuation Now it's time for you to practice what you've leamed. Suppose that the firm recently paid a dividend $2.20. It expects to have nonconstant growth of 11% for 3 years and then a constant rate of 3% thereafter. The firm's required return is 10%. The firm's horizon, or continuing, value is and its intrinsic value today is Accurate estimates of future dividends are not easily available. For some companies it is reasonable to assume that dividends will grow at a constant rate. However, most firms go through life cycles where they experience different growth rates during different parts of the cycle. In their early years, most firms grow much faster than the economy as a whole; then they match the economy's growth; and finally they grow at a slower rate than the economy. These firms are called supernormal, or nonconstant, growth firms. The value of this firm's stock, like any other asset, is the present value of its expected future dividends as determined by Value of stock, P0=PV of expected future dividends =(1+r1)tD1+(1+E1)1D1++(1+r1)2D2=1=1(1++yyD1 When D1 is growing at a constant rate, you can simplify the previous equation as follows: P0=f11D1 In the supernormal case, however, the expected growth rate is not a constant, seil, you can combine both equations to construct a new formula for valuing the stock. First, assuming that a company currently enjoying supernormat growth will slow down in N periods ( N is often called the horizon, or terminal, date) and then will grow at a constant rate, g. Second, you can use the constant growth formula to determine what the stock's horizon value will be N periods from totay: Horizon walue, PN=h1rDm=1. Pverharian vatwe, FN To find the stock's intrinsic value, you need to go through the following three steps: 1. Find the PV of each dividend during the period of nonconstant growth and sum them. 2. Find the expected stock price at the end of the nonconstant growth period. At this point it has become a constant gcowth stock, so it can be valued with the constant growth model. Discount this price back to the present. 3. Add these components to find the stock's intrinsic value, P0. 3-year nonconstant growth period is grr=11%, the normal growth rate after the fionconstant period, l.t.y startifg at the end of year three and in the future is ge=4%, and the required (minienum acceptable) rate of return on the stock is ra=10%. What is the formuta for the stock's intrinsic volide in this case? Pverharian vatwe, FN To find the stock's intrinsic value, you need to go through the following three steps: 1. Find the PV of each dividend during the period of nonconstant growth and sum them. 2. Find the expected stock price at the end of the nonconstant growth period. At this point it has become a constant gcowth stock, so it can be valued with the constant growth model. Discount this price back to the present. 3. Add these components to find the stock's intrinsic value, P0. 3-year nonconstant growth period is grr=11%, the normal growth rate after the fionconstant period, l.t.y startifg at the end of year three and in the future is ge=4%, and the required (minienum acceptable) rate of return on the stock is ra=10%. What is the formuta for the stock's intrinsic volide in this case? Suppose that the firm recently paid a dividend D0=$2.20. It expects to have nonconstant growth of gs=11% for 2 years and then a constant rate of gn=3% thereafter. The firm's required return is rs=10%. According to the problem walk-through video, what is the formula for the terminal, or continuing value, at the end of year 2 ? P2=r1rD2P2=(1+r1)2D2P2=(1+r1)3D2P2=r1tD1 According to the problem walk-through video, what is the formula for the firm's intrinsic value today? P0=(1+t1)2P2P0=(1+r2)2D1+(1+r2)2D2+(1+r2)2D1+(1+r1)2P2P0=(1+r1)2D1+(1+r1)2D1+(1+r0)2P1P0=(1+r2)2D1+(1++1)2D1+P2 Suppose that the firm recently paid a dividend D0=$2.20. It expects to have nonconstant growth of gs=11% for 2 years and then a constant rate of gn=3% thereafter. The firm's required return is rs=10%. According to the problem walk-through video, what is the formula for the terminal, or continuing value, at the end of year 2 ? P2=r1rD2P2=(1+r1)2D2P2=(1+r1)3D2P2=r1tD1 According to the problem walk-through video, what is the formula for the firm's intrinsic value today? P0=(1+t1)2P2P0=(1+r2)2D1+(1+r2)2D2+(1+r2)2D1+(1+r1)2P2P0=(1+r1)2D1+(1+r1)2D1+(1+r0)2P1P0=(1+r2)2D1+(1++1)2D1+P2 The firm's horizon value is The firm's intrinsic value is Step 3: Practice: Nonconstant Growth Valuation Now it's time for you to practice what you've leamed. Suppose that the firm recently paid a dividend $2.20. It expects to have nonconstant growth of 11% for 3 years and then a constant rate of 3% thereafter. The firm's required return is 10%. The firm's horizon, or continuing, value is and its intrinsic value today is The firm's horizon value is The firm's intrinsic value is Step 3: Practice: Nonconstant Growth Valuation Now it's time for you to practice what you've leamed. Suppose that the firm recently paid a dividend $2.20. It expects to have nonconstant growth of 11% for 3 years and then a constant rate of 3% thereafter. The firm's required return is 10%. The firm's horizon, or continuing, value is and its intrinsic value today is