Activity 1

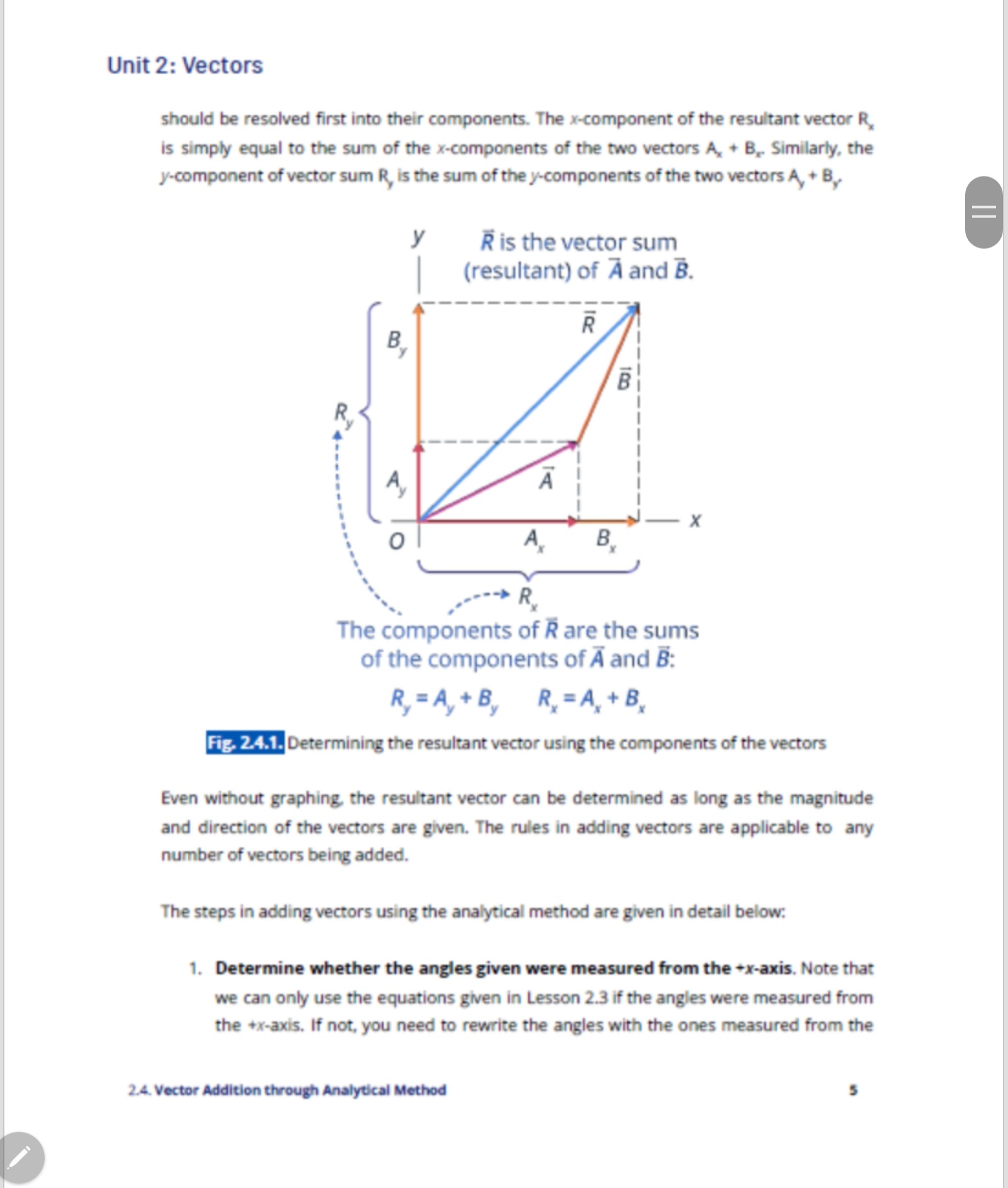
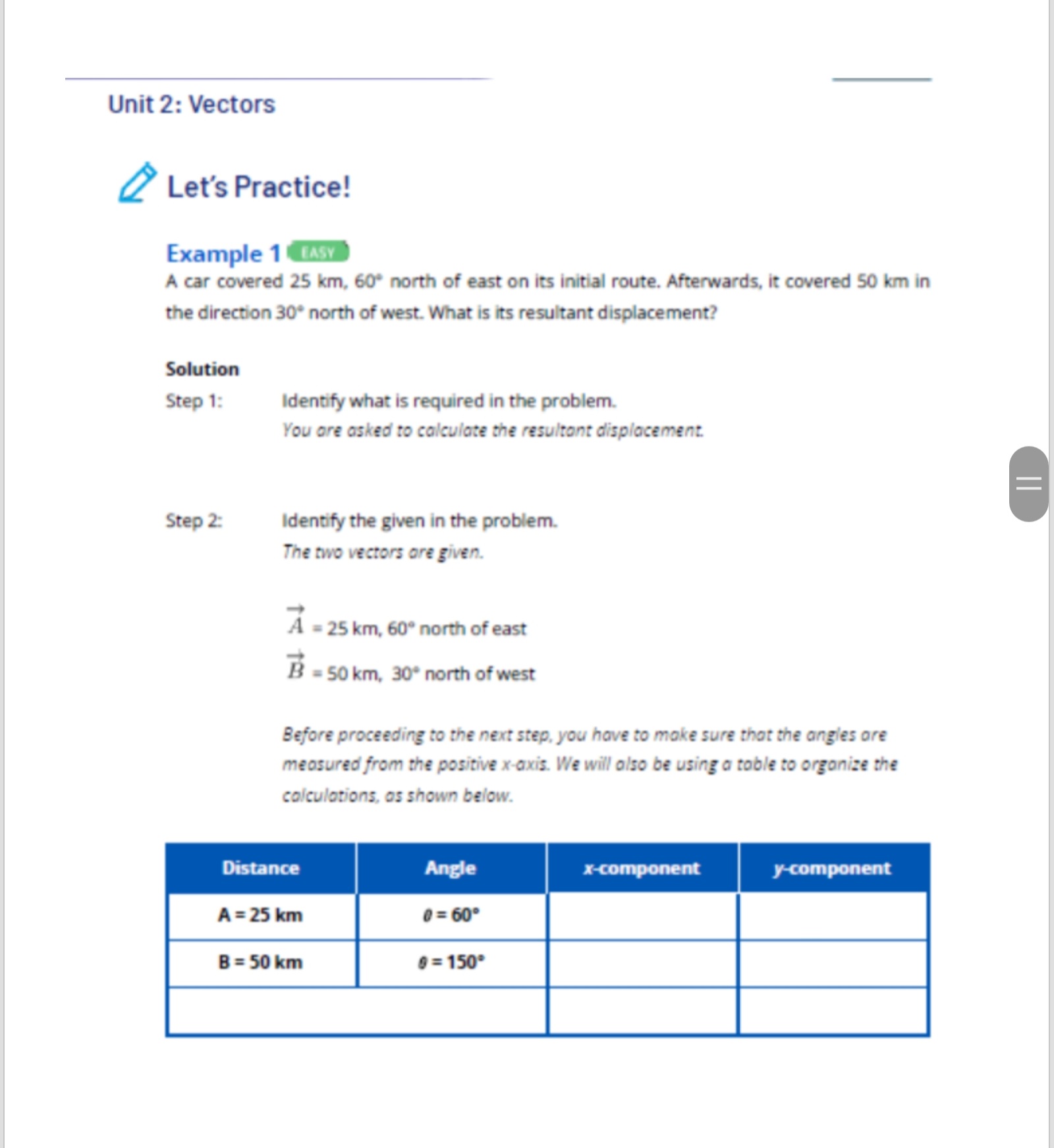
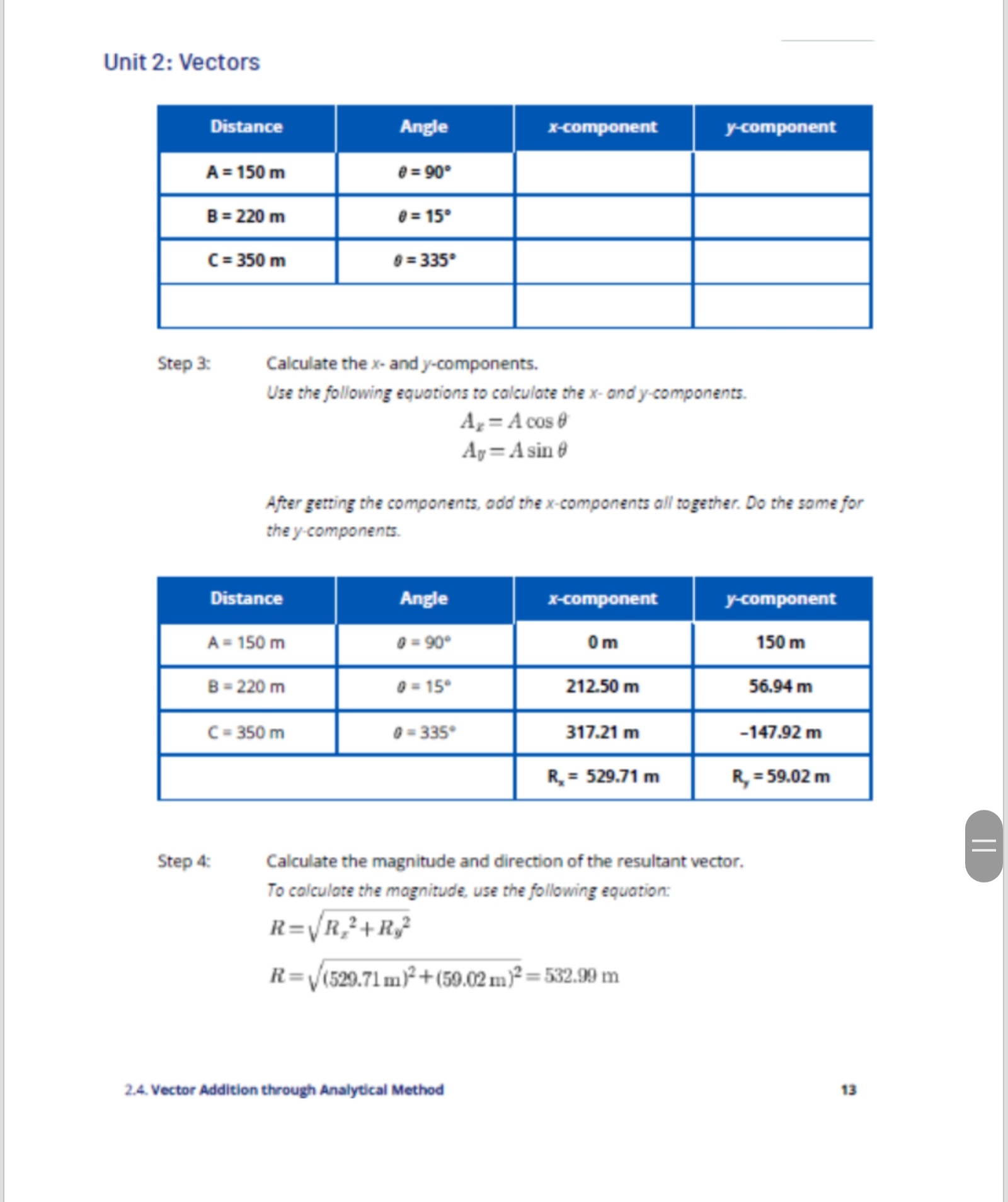
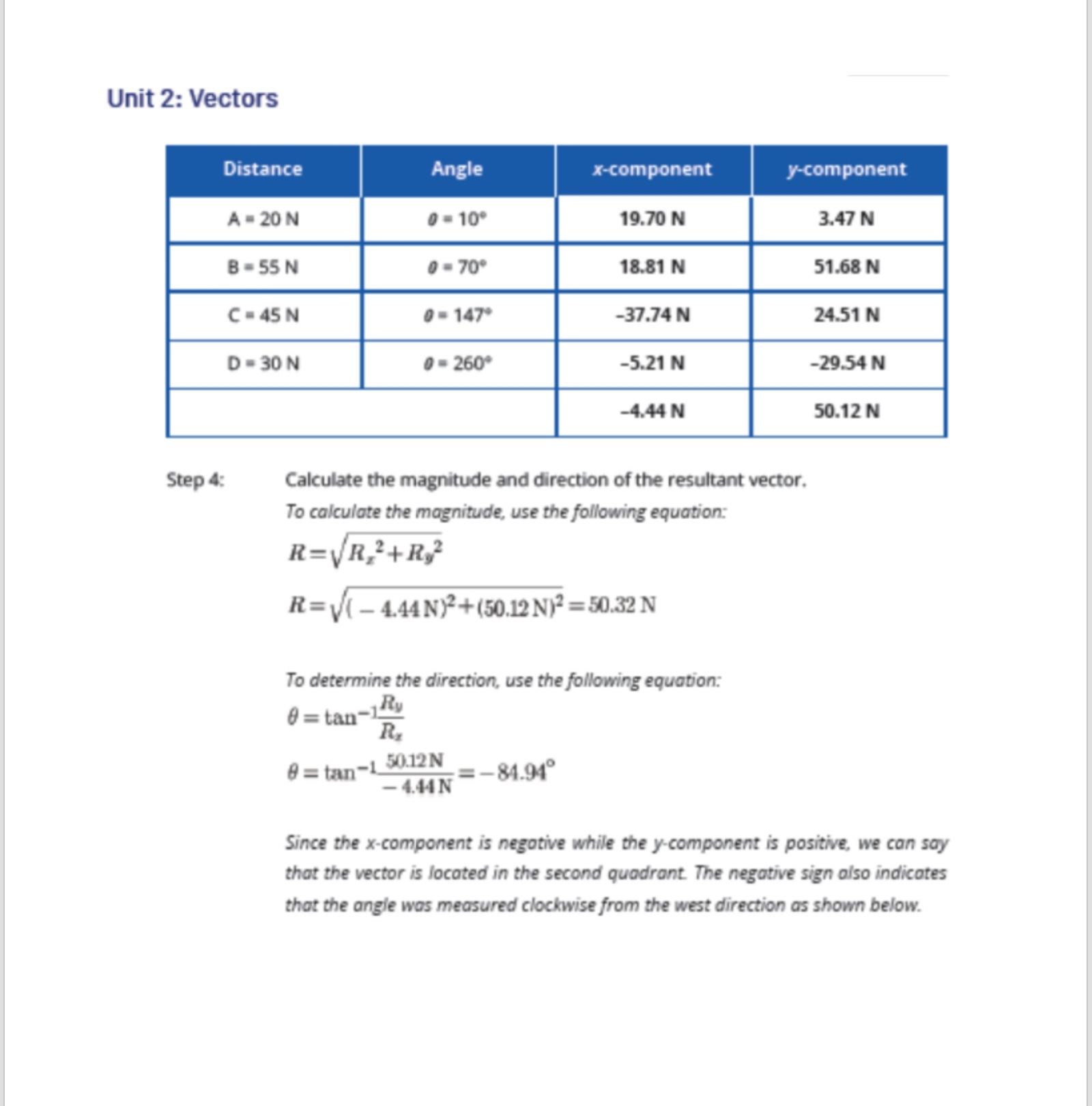
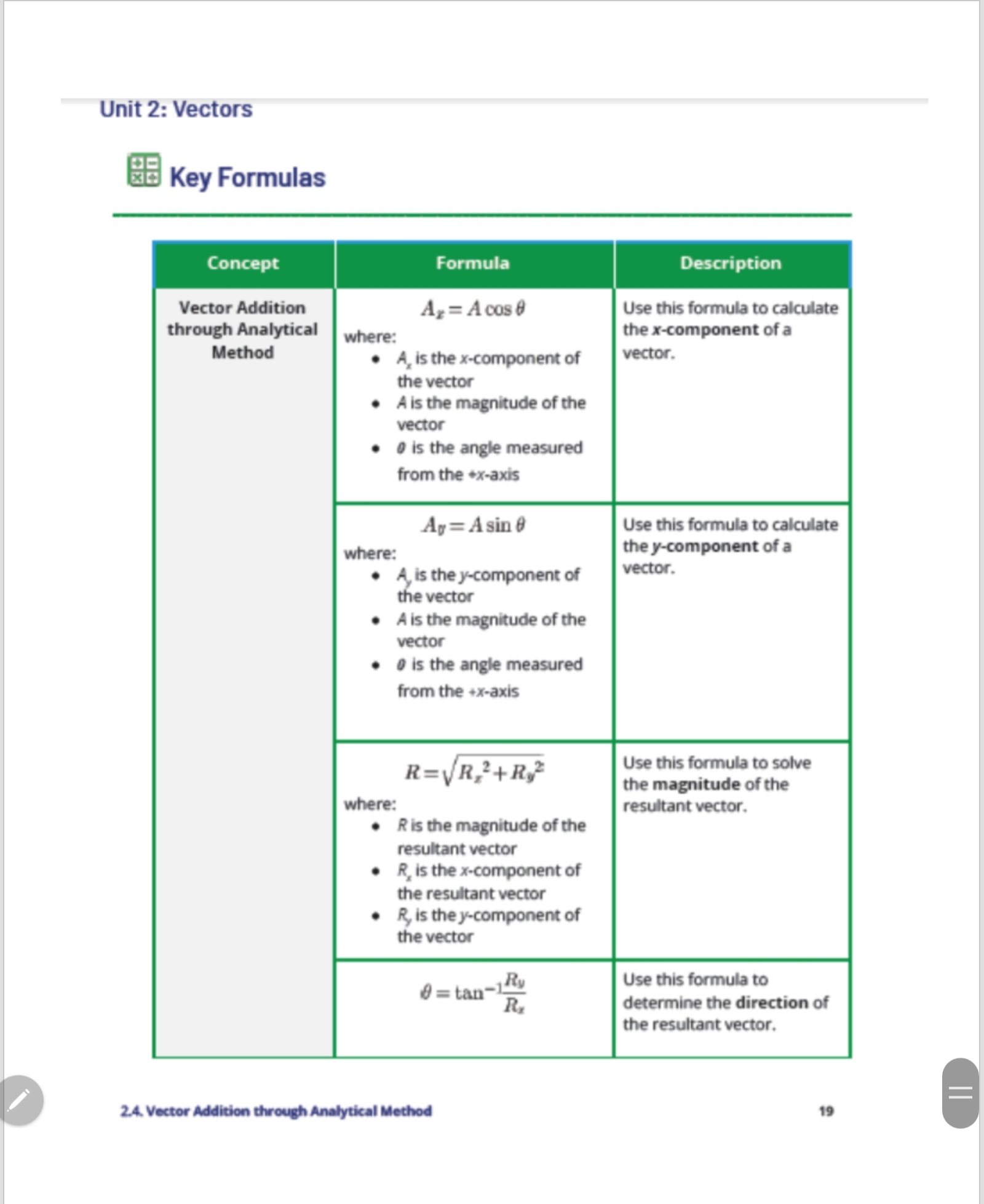
Check Your Understanding A. Write the correct word(s) in the space provided to complete the UNDERSTAND sentence. 1. The function is used to calculate the x-component of a vector. 2. The function is used to calculate the y-component of a vector. 3. The function is used to calculate the direction of the resultant vector. 4. is used to calculate the magnitude of the resultant vector. 5. The x-component of the resultant vector is equal to the of the x-components of all the vectors. 6. The y-component of the resultant vector is equal to the sum of the of all the vectors. 7. To be able to use the equations, the angle should be measured from the 8. The analytical method involves adding the of the vectors. 9. The analytical method is more accurate than the of adding vectors. 10. If the x-component is positive and the y-component is negative, the resultant vector is most likely located in the quadrant.Unit 2: Vectors B. Calculate the resultant vector using the analytical APPLY method. 1. A = 10 km, north; B = 15 km, east 2. C - 6 m/s', 100-; D- 9 m/s'. 220- 3. A - 650 N, 270; 1 - 550 N, 320 north of west 4. A = 130 m, 19" north of east; B= 200 m, 70 north of east 5. A = 22 m/s, 70 north of west: B = 53 m/s, 60 south of east 6. A = 2500 m, east: B - 1500 m, north; C' = 1850 m, 45* north of west 7. A = 70 m, 30 east of north; 1 = 55 m. 40* south of west; C' = 20 m, south 8. A = 25 km, 45 south of east; B - 50 km. 65* west of south; C' = 50 km, 5 south of west 9. A=13 N, north: B-20 N, east, = 30 N, north; D=10 N, 45- 10. A = 150 m/s, 75; B - 213 m/s, 21* west of north; C' = 396 km/h, 75* north of west; D-288 km/h, 10 south of westUnit 2: Vectors Lesson 2.4 Vector Addition through Analytical Method MAHLE GOODS NAL EA 08. Introduction A race car being pushed on a pavement shown in the image above experiences a lot of forces acting on it. Some of these forces include the car's weight, the frictional force acting between the tires and the pavement, and the forces exerted at an angle by the individuals pushing it. The sum of these forces will determine whether the car will move or not. You learned in the past lesson that vectors can be added using the graphical method, but what if you do not have enough time to sketch or draw in a graphing paper? Is there any other way to determine the resultant force acting on the race car above? Can you also even find the resultant displacement covered by a person or a vehicle? In this lesson, you will learn about vector addition using the analytical method. 2.4. Vector Addition through Analytical MethodUnit 2: Vectors Learning Objectives DepEd Competency In this lesson, you should be able to do the Perform addition of vectors following: (STEM_GP12V-13-9). . Understand the rules in adding vectors using the analytical method. Add two or more vectors using the analytical method. Warm Up Pair Up! 10 minutes In this lesson, you will be practicing determining the components of a vector and getting the vector given its components. This will serve as a jumpstart in order for you to easily grasp the discussion afterwards. Materials . list of five vectors and five pairs of x- and y-components . strips of paper containing the values which correspond to the list of vectors and components tape calculator paper pen or pencil 2.4. Vector Addition through Analytical MethodUnit 2: Vectors Guide Questions 1. How are the x- and y-components calculated? 2. How did you calculate the magnitude and the resultant of the vector? 3. Suppose you have to add the vectors in each set, is there any way to add it aside from the graphical method? How will you do it? Learn about It! The graphical method is very helpful in visualizing vector addition. It is also easier to determine the correct direction of the resultant vector using this method. However, it is time consuming since you need to represent each vector correctly through graphing. As mentioned in the previous lessons, the graphical method is also prone to errors since it is highly dependent on the precision of the measuring devices that will be used. That is why most of the time, vectors are added using the analytical method or component method. It uses trigonometric functions and Pythagorean theorem. ? How are vectors added using the analytical method? Adding Vectors Using the Analytical Method Consider the word problem below. We will be using this problem as we continue with the discussion. Denise walks every day from her house to the school. First, she covers 10 m, 20 north of east. Then, she walked 15 m in a direction 50 north of east. What is her resultant displacement? Aside from the graphical method, the two displacement vectors can be added using the analytical or component method. Let us label the two displacement vectors in the problem as A and B. with a vector sum F, as shown in Fig, 2.4.1. To add these two vectors, they 2.4. Vector Addition through Analytical MethodUnit 2: Vectors should be resolved first into their components. The x-component of the resultant vector R is simply equal to the sum of the x-components of the two vectors A, + B,. Similarly, the y-component of vector sum R, is the sum of the y-components of the two vectors A, + By R is the vector sum (resultant) of A and B. R B B R A X A The components of R are the sums of the components of A and B: R = A +B R. = A, +B, Fig. 2.4.1. Determining the resultant vector using the components of the vectors Even without graphing, the resultant vector can be determined as long as the magnitude and direction of the vectors are given. The rules in adding vectors are applicable to any number of vectors being added. The steps in adding vectors using the analytical method are given in detail below: 1. Determine whether the angles given were measured from the +x-axis. Note that we can only use the equations given in Lesson 2.3 if the angles were measured from the +x-axis. If not, you need to rewrite the angles with the ones measured from the 2.4. Vector Addition through Analytical MethodUnit 2: Vectors said axis. As what was used in the past lessons, we will also measure the angle from the +x-axis in a counterclockwise direction. It would also be helpful to use a table, as shown in Table 2.4.1, to have an organized way of adding vectors. Let us consider the given word problem. Displacement vector A is equal to 10 m. 20' north of east, while vector B is 15 m, 50" north of east. Since they are measured from the east to the north direction, you can automatically say that these angles were measured from the +x-axis and can be used as 0 in the next steps. However, it is also helpful to draw or sketch the direction of the vectors as shown in Fig. 2.4.2 From the figure, you can confirm that both angles are measured from the +x-axis. 20 A B Fig. 2.4.2. Directions of vectors A and B 2. Resolve each vector into its x- and y-components. Use the cosine function to calculate the x-component, and the sine function to determine the y-component. Take note of the signs of the components because this will largely affect the result of your calculations in the latter part. Use Equation 2.4.1 and Equation 2.4.2 to determine the x- and y-components of the vector.Unit 2: Vectors Ar= A cos 0 Equation 2.4.1 Ay = Asin Equation 2.4.2 As shown in Table 2.4.1, the x- and y-components of both vectors in the problem were calculated using the given equations. 3. Add all the x-components together. Do the same for all the y-components. The sum of both components are the components of the resultant vector, R, and Ry Table 2.4.1. Calculations for the x- and y-components of the resultant vector Distance Angle x-component y-component A = 10 m 0 = 20 9.40 m 3.42 m B = 15 m 0 = 50 9.64 m 11.49 m R. = 19.04 m R = 14.91 m 4. Calculate the magnitude of the vector using the Pythagorean theorem, given in the equation below: R=VR,2+R,? Equation 2.4.3 Using the given R, and Ry, we can now calculate the magnitude of the resultant vector R. R=VR,2+Ry2=\\(19.04m)?+(14.91m)? = 24.18m The magnitude of the resultant vector is equal to 24.18 m. 2.4. Vector Addition through Analytical MethodUnit 2: Vectors 5. Calculate the angle : using the inverse tangent function using Equation 2.4.4 8 = tan-1Ry Equation 2.4.4 E Note that the angle you will get from the equation is not necessarily the angle measured from the +x-axis. It is important to check the signs of the x- and y- components since they indicate the position of the vector in the Cartesian plane. Using the given quantities, we can now calculate the angle 0. Rz 0 = tan-129 = tan-11451m = 38.06" 19.04 m The vector is located in the first quadrant since both the x- and y-components are positive. Therefore, the angle 38.06' is also the direction of the vector as measured from the +x-axis. The resultant vector of Denise is 24.18 m, 38.06' or 38.06* north of east. W Remember Always check whether your calculator is in the degree mode before proceeding to the calculations. All your calculations would be different if this is not addressed beforehand.Unit 2: Vectors Let's Practice! Example 1 EASY A car covered 25 km, 60" north of east on its initial route. Afterwards, it covered 50 km in the direction 30' north of west. What is its resultant displacement? Solution Step 1: Identify what is required in the problem. You are asked to calculate the resultant displacement. Step 2: Identify the given in the problem. The two vectors are given. A = 25 km, 60 north of east B - 50 km, 30* north of west Before proceeding to the next step, you have to make sure that the angles are measured from the positive x-axis. We will also be using a table to organize the calculations, as shown below. Distance Angle x-component y-component A =25 km 0 = 60 B =50 km 0 = 150Unit 2: Vectors Step 3: Calculate the x- and y-components. Use the following equations to calculate the x- and y-components. Ar = A cos Ay = Asin 0 After getting the components, add the x-components all together. Do the same for the y-components. Distance Angle x-component y-component A = 25 km 0 = 60 12.50 km 21.65 k m B =50 km 0 = 150 -43.30 km 25 km R, = -30.80 km R, = 46.65 km Step 4: Calculate the magnitude and direction of the resultant vector. To calculate the magnitude, use the following equation: R=VR,2+R,2 R=V( - 30.80 km)2+(46.65 km)? =55.90 km To determine the direction, use the following equation: 8 = tan-1Ry 0 = tan-1 46.65 km =-56.57 - 30.80 km Since the x-component is negative while the y-component is positive, we can say that the vector is located in the second quadrant. The negative sign also indicates that the angle was measured clockwise from the west direction, as shown in the figure below.Unit 2: Vectors 56.57 7 123.430 Tips Draw or sketch the resultant vector in a Cartesian plane especially if one or both of the x- and y-components are negative. It would help you visualize the correct and final direction of the resultant vector. If you have time to spare, you can also use the graphical method of addition of vectors to check whether your final answer is correct or not. Step S: Find the answer. R = 55.90 km 0 = 123.43 or 56.57' north of west The resultant displacement is 55.90 km, 123.43' or 56.57 north of west.Unit 2: Vectors 1 Try It! EASY During his early morning training, Louie jogged 10 km, 20 south of west. He then covered another 15 km in the direction of 60 south of east before resting. What is his resultant displacement? Example 2 AVERAGE A person covered three displacement vectors as follows: A = 150 m north; B = 220 m. 15- north of east and; C' = 350 m, 25* south of east. What is his resultant displacement? Solution Step 1: Identify what is required in the problem. You are asked to calculate the resultant displacement. Step 2: Identify the given in the problem. Three vectors are given. A = 150 m, north B - 220 m, 150 north of east C = 350 m, 25* south of east Before proceeding to the next step, you have to make sure that the angles ore measured from the positive x-axis. We will also be using a table to organize the calculations, shown as follows. 2.4. Vector Addition through Analytical Method 12Unit 2: Vectors Distance Angle x-component y-component A = 150 m 0 = 90 B = 220 m 0 = 15 C = 350 m 0 = 335 Step 3: Calculate the x- and y-components. Use the following equations to calculate the x- and y-components. Ar = A cos Ay = Asin 0 After getting the components, add the x-components all together. Do the same for the y-components. Distance Angle x-component y-component A = 150 m 0 = 90 0m 150 m B = 220 m 0 = 15 212.50 m 56.94 m C = 350 m 0 = 335 317.21 m -147.92 m R, = 529.71 m R, =59.02 m Step 4: Calculate the magnitude and direction of the resultant vector. To calculate the magnitude, use the following equation: R=VR,2+R,? R=\\(529.71 m)?+(59.02 m)? =532.99 m 2.4. Vector Addition through Analytical Method 13Unit 2: Vectors To determine the direction, use the following equation: 0 = tan-1/ty R. 8 = tan-1 59.02m = 6.36' 529.71 m Since both the x- and y-components are both positive, we can say that the vector is located in the first quadrant. The positive sign also indicates that the angle was measured counterclockwise from the east (+x-axis) direction. Step 5: Find the answer. R = 532.99 m 0 = 6.36* or 6.36' north of east The resultant displacement is 532.99 m, 6.36' or 6.36 north of east. 2 Try It! AVERAGE Find the resultant vector R. if A is 95 N. 30 north of east. B is 50 N, south while C has a magnitude of 75 N and a direction of 45 south of west. Example 3 DIFFICULT Four sled dogs are pulling a 1000 kg load. Sled dog A is pulling the load at 20 N, 10" north of east. Sled dog B is pulling the load at 55 N, 70 north of east. Sled dog C is pulling the load at 45 N. 33 north of west, while sled dog D exerts 30 N at a direction of 80* south of west. What is the resultant force acting on the load? Solution Step 1: Identify what is required in the problem. You are asked to calculate the resultant force. 2.4. Vector Addition through Analytical Method 14Unit 2: Vectors Step 2: Identify the given in the problem. Four vectors are given. A = 20 N, 10 north of east B = 55 N. 70 north of east C = 45 N, 33* north of west D = 30 N, 80 south of west Before proceeding to the next step, you have to make sure that the angles are measured from the positive x-axis. We will also be using a table to organize the calculations, as shown below. Distance Angle x-component y-component A = 20 N 0 = 10 B =55 N 8 = 70 C =45 N 9 = 147' D = 30 N 8 = 260 Step 3: Calculate the x- and y-components. Use the following equations to calculate the x- and y-components. Ay = A cos 0 Ay = Asin 0 After getting the components, add the x-components all together. Do the same for the y-components. 2.4. Vector Addition through Analytical Method 15Unit 2: Vectors Distance Angle x-component y-component A = 20 N 0 = 10 19.70 N 3.47 N B - 55 N 0 = 70 18.81 N 51.68 N C = 45 N 0 = 147 -37.74 N 24.51 N D - 30 N 0 = 260 -5.21 N -29.54 N -4.44 N 50.12 N Step 4: Calculate the magnitude and direction of the resultant vector. To calculate the magnitude, use the following equation: R=VR,2+R,2 R=V( - 4.44N)+(50.12 N)? = 50.32 N To determine the direction, use the following equation: 8 = tan-1Ry 8 = tan-1 50.12N -4.44N =-84.940 Since the x-component is negative while the y-component is positive, we can say that the vector is located in the second quadrant. The negative sign also indicates that the angle was measured clockwise from the west direction as shown below.Unit 2: Vectors 84.940 95.060 Step 5: Find the answer. R = 50.32 N 0 = 95.06' or 84.94' north of west The resultant force is 50.32 N. 95.06' or 84.94' north of west. 3 Try It! DIFFICULT A plane covered four routes with the following velocities: A - 50 m/s, 30 south of east B - 20 m/s, 60 south of west C - 70 m/s, 25* south of west D - 65 m/s, 15 north of west What is the resultant velocity of the plane? 2.4. Vector Addition through Analytical Method 17How can you check whether the angle @ from the Inverse tangent function was measured from the +x-axis? Key Points . The analytical method of adding vectors utilizes the trigonometric functions and the Pythagorean theorem. It is more accurate and less time consuming than the graphical method. . Before resolving the components, ensure first that the angle is measured from the +x-axis. . The following are the steps to add vectors using the analytical method: 1. Calculate the x- and y-components of all the vectors. Use the cosine function to calculate the x-component, and the sine function to determine the y-component. 2. After this, add all the x-components together. Do the same for the y-components. The sums are the x- and y-components of the resultant vector. 3. Use the Pythagorean theorem to determine the magnitude of the resultant vector. 4. Use the inverse tangent function to determine the direction of the resultant vector. Check first whether the angle . from your calculation is measured from the +x-axis or not. Express it in the correct notation.Unit 2: Vectors Key Formulas Concept Formula Description Vector Addition Ar = A cos 8 Use this formula to calculate through Analytical where: the x-component of a Method A, is the x-component of vector. the vector A is the magnitude of the vector 0 is the angle measured from the *x-axis Ay = Asin 0 Use this formula to calculate where: the y-component of a A, is the y-component of vector. the vector A is the magnitude of the vector 0 is the angle measured from the +x-axis R=VR,2+R,2 Use this formula to solve the magnitude of the where: resultant vector. R is the magnitude of the resultant vector R, is the x-component of the resultant vector R, is the y-component of the vector 8 = tan-1Ry Use this formula to determine the direction of the resultant vector. 2.4. Vector Addition through Analytical MethodUnit 2: Vectors where: is the angle . R, is the x-component of the resultant vector R, is the y-component of the resultant vector