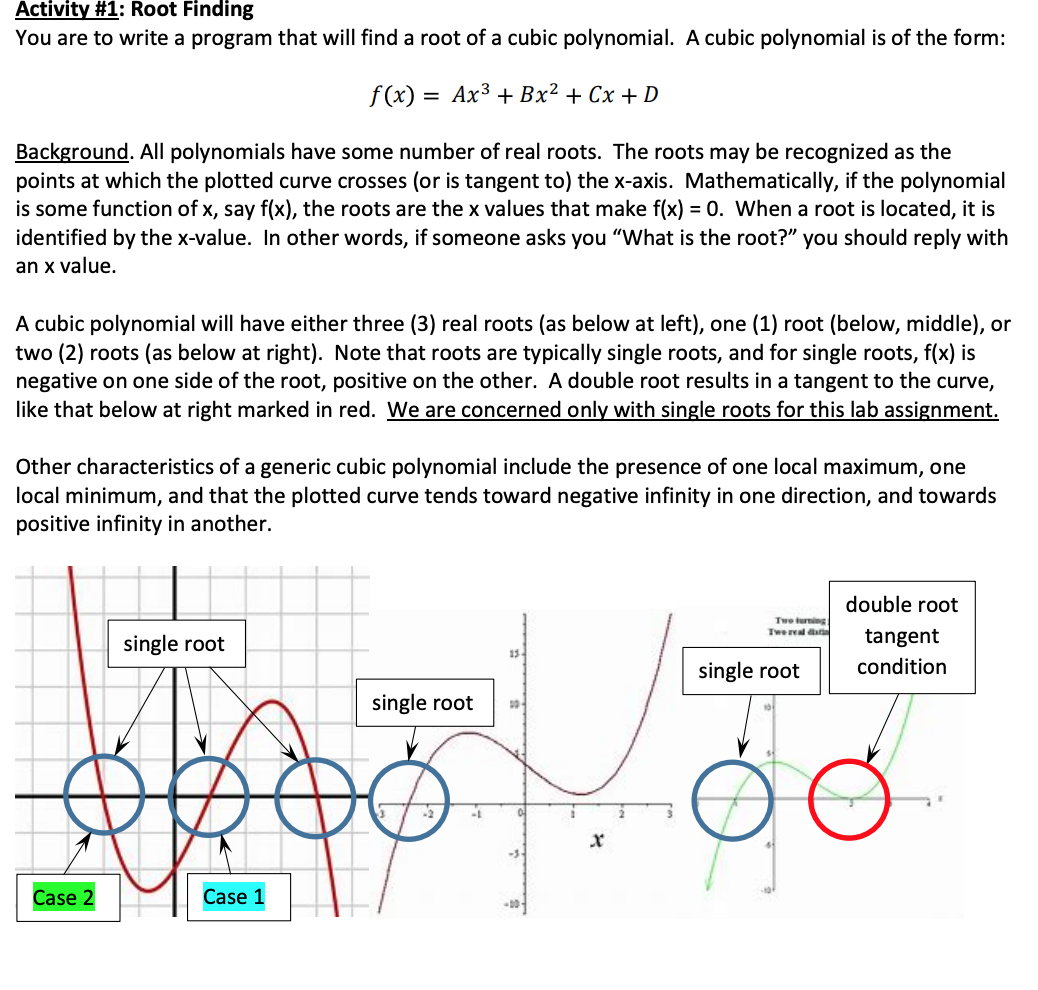
Activity #1: Root Finding You are to write a program that will find a root of a cubic polynomial. A cubic polynomial is of the form: f(x) = Ax3 + Bx2 + Cx + D Background. All polynomials have some number of real roots. The roots may be recognized as the points at which the plotted curve crosses (or is tangent to) the x-axis. Mathematically, if the polynomial is some function of x, say f(x), the roots are the x values that make f(x) = 0. When a root is located, it is identified by the x-value. In other words, if someone asks you "What is the root?" you should reply with an x value. A cubic polynomial will have either three (3) real roots (as below at left), one (1) root (below, middle), or two (2) roots (as below at right). Note that roots are typically single roots, and for single roots, f(x) is negative on one side of the root, positive on the other. A double root results in a tangent to the curve, like that below at right marked in red. We are concerned only with single roots for this lab assignment. Other characteristics of a generic cubic polynomial include the presence of one local maximum, one local minimum, and that the plotted curve tends toward negative infinity in one direction, and towards positive infinity in another. Tweter Tweede single root double root tangent condition single root single root 100,00 Case 2 Case 1 A Method for Finding a Single Root: Now that we know all about loops, we may be tempted to simply compute f(x) for a large number of x values and determine when f(x) == 0. However, due to floating point error, we will almost never find a root using this method. At best, this would be unreliable. One reliable method for finding a single root uses a bisection procedure. With this method, we are trying to find an interval on x such that the root lies in this interval, but the interval width is very small. (Remember tolerances?) So, we are not trying to find a value of x such that f(x) is exactly zero. Instead, we are trying to find an interval on x which contains the root and which is of arbitrarily small width. Let's assume that we know that a single root lies between x = a and x = b. We can express this interval as [a,b]. Let's also assume that we know that a 0, replace b such that the new interval is [a,p). e. Note that after the bisection, the interval is half the width of the previous interval. f. Continue this procedure until we find an interval of width0, replace a such that the new interval is [p,b]. ii. If f(p= a+1). Your team needs to find examples of cubic polynomials for which you know the roots. Google may prove useful for that. Your code should include documentation of these four (or more) test cases in comments, near the top of the program (after your standard header). Use the posted Python code to plot your cubic polynomial and determine appropriate values for a and b. You should create a program that performs bisection to determine a single root of a cubic polynomial. More specifically, your program should do the following: Print a message indicating the purpose of the program and simple instructions. Read in the coefficients of the cubic polynomial from the user via the keyboard Read in the upper and lower bounds of an interval on x that includes a single root of the cubic polynomial. (These are the values a and b from above.) O Plot the curve and choose a and b such that you know that a single root exists on that interval. Your code does not have to search for an appropriate interval. Determine the value of that root to within 10-6 tolerance Print the value of the root found as a single number with appropriate label Print out how many iterations it took to find that root. Include appropriate comments in your code so that we can follow your logic. Also, as stated above, include the detail of your four test cases in comments just under the header information