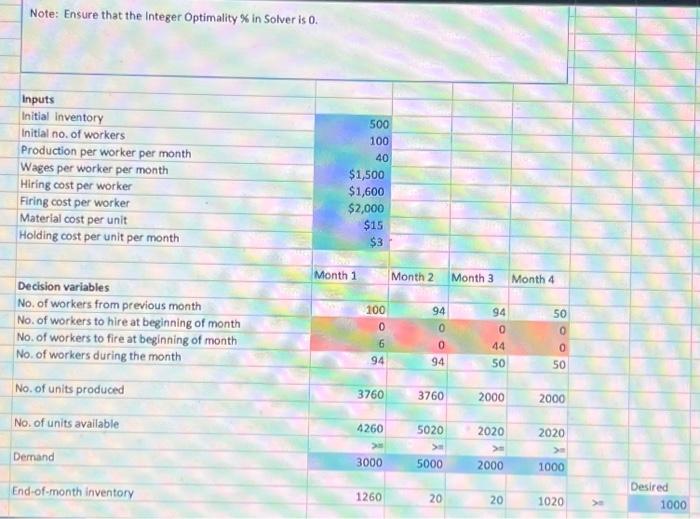
Aggregate planning Reconsider the shoe manufacturer problem of Session 10. Its speadsheet model is reproduced below for your convenience. The Solver parameters are also embedded in this worksheet. Change the spreadsheet model to include the following: If necessary, a worker can produce up to 5 pairs of shoes during overtime in each month. A worker is paid $52 per pair of shoes produced during overtime. a. Change the spreadsheet model and re-solve it using Solver. b. Compare the optimal solutions with (this problem) and without overtime (the problem in Session 10). What is the difference? Does the difference make sense? Briefly explain. Hints: 1. Insert 2 rows in Inputs for Maximum overtime production per worker per month and Overtime production cost per unit 2. Insert 4 rows below the row containing No. of workers during the month i. Dedicate a row to decision variables for No. of units to produce in overtime during each month ii. Dedicate a row to Maximum no. of units to produce in overtime during each month and enter the formulas for these. Note that these depend on the No. of workers during the month and Maximum overtime production per worker per month 3. Change the No, of units produced to include the overtime production 4. Insert a row in Output and add the overtime cost 5. In Solver Parameters window, add overtime production cells as decision variables (in addition to no. of hires and fires) and add the max OT production constraints. Note: Ensure that the Integer Optimality \% in Solver is 0. Note: Ensure that the Integer Optimality % in Solver is 0. \begin{tabular}{|lr|} \hline Output & \\ \hline Hiring cost & $0 \\ \hline Firing cost & $100,000 \\ \hline wage cost & $432,000 \\ \hline Material cost & $172,800 \\ \hline Holding cost & $6,960 \\ \hline Total cost & $711,760 \\ \hline \end{tabular}