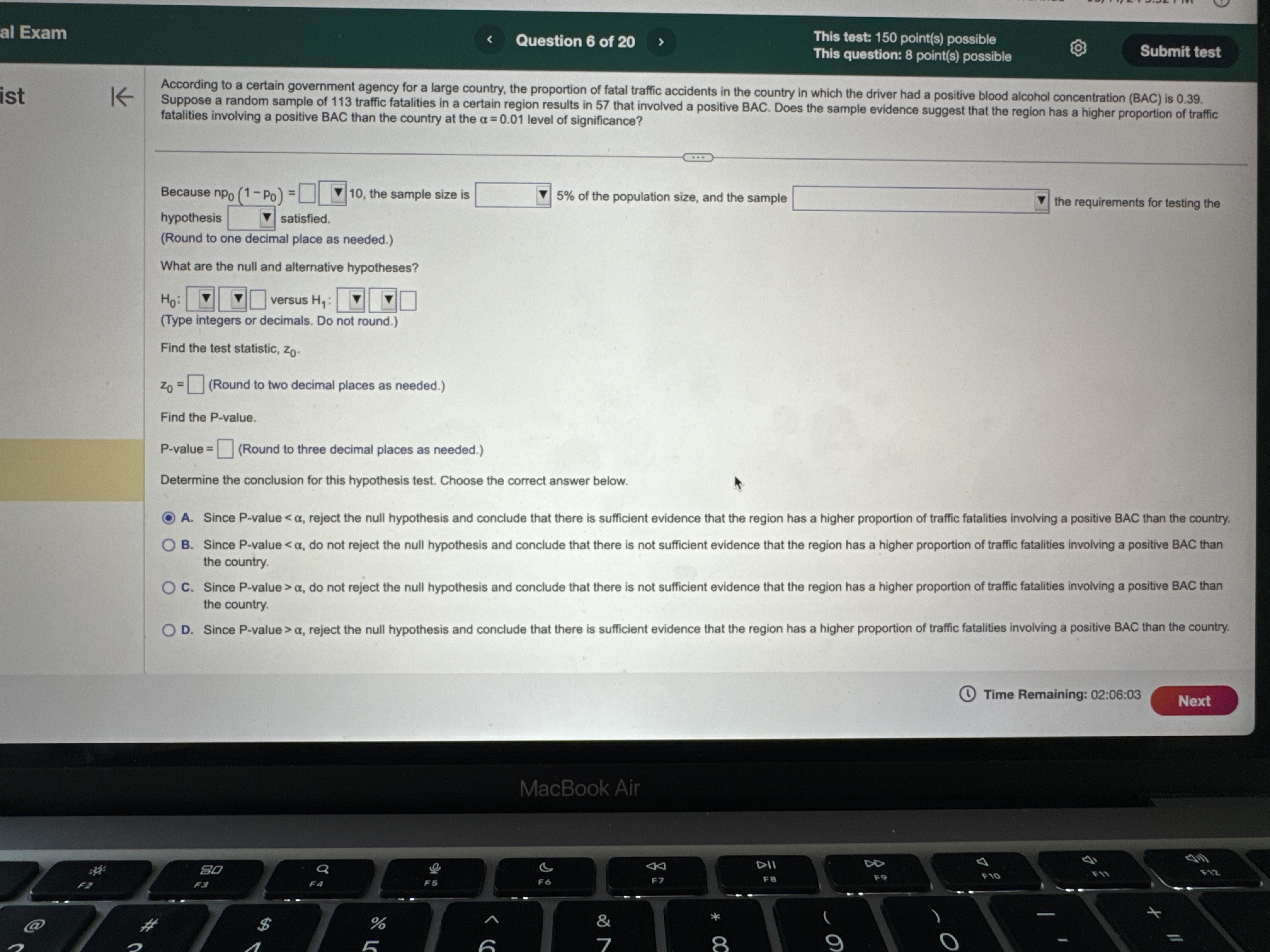
al Exam e T L L This test: 150 point(s) possible This question: 8 point(s) possible & EIL LR According to a certain government agency for a large country, the proportion of fatal traffic accidents in the country in which the driver had a positive blood alcohol concentration (BAC) is 0.39. Suppose a random sample of 113 traffic fatalities in a certain region results in 57 that involved a traffic F L c I positive BAC. Does the sample evidence i i proportion fatalities involving a positive BAC than the country at the a = 0.01 level of significance? 8 e e LS 3 B i = _ S 2 S 3 Because np, %1 = Po) = E}'IO. the sample size is [RER V| 5% of the population size, and the sample [ & V] the requirements for testing the hypothesis satisfied. (Round to one decimal place as needed.) What are the null and alternative hypotheses? r =T Ho: | [V V']versus H, ' V} Vl (Type integers or decimals. Do not round.) Find the test statistic, z, z5= j (Round to two decimal places as needed.) Find the P-value P-value = {L} (Round to three decimal places as needed.) Determine the conclusion for this hypothesis test. Choose the correct answer below A @ A. Since P-value a, do not reject the null hypothesis and conclude that there is not sufficient evidence that the region has a higher proportion of traffic fatalities involving a positive BAC than the country. O D. Since P-value > a, reject the null hypothesis and conclude that there is sufficient evidence that the region has a higher proportion of traffic fatalities involving a positive BAC than the country: R e e NGy @ Time Remaining: 02:06:03 m Exam Question 8 of 20 This test: 150 point(s) possible This question: 10 point(s) possible st K The data below represent commute times (in minutes) and scores on a well-being survey. Complete parts (a) through (d) below. Commute Time (minutes), x 5 20 25 35 60 84 105 Well-Being Index Score, y 69.1 67.6 67.0 66.3 64.5 63.6 61.4 (a) Find the least-squares regression line treating the commute time, x, as the explanatory variable and the index score, y, as the response variable. y = [ x + 0) (Round to three decimal places as needed.) (b) Interpret the slope and y-intercept, if appropriate. First interpret the slope. Select the correct choice below and, if necessary, fill in the answer box to complete your choice. A. For a commute time of zero minutes, the index score is predicted to be (Round to three decimal places as needed.) O B. For every unit increase in index score, the commute time falls by , on average. (Round to three decimal places as needed.) O C. For an index score of zero, the commute time is predicted to be minutes. (Round to three decimal places as needed.) O D. For every unit increase in commute time, the index score falls by , on average. (Round to three decimal places as needed.) O E. It is not appropriate to interpret the slope. Interpret the y-intercept. Select the correct choice below and, if necessary, fill in the answer box to complete your choice. O A. For an index score of zero, the commute time is predicted to be minutes. (Round to three decimal places as needed.) O B. For every unit increase in commute time. the index score falls bv . on average. Time Remaining: 02 MacBook AirThe data below represent commute times (in minutes) and scores on a well-being survey. Complete parts (a) through (d) below. Commute Time (minutes), x 5 20 25 35 60 84 105 Well-Being Index Score, y 69.1 67.6 67.0 66.3 64.5 63.6 61.4 interpret the y-intercept. Select the correct choice below and, IT necessary, fill in the answer box to complete your choice. A. For an index score of zero, the commute time is predicted to be minutes. (Round to three decimal places as needed.) O B. For every unit increase in commute time, the index score falls by , on average. Round to three decimal places as needed.) O C. For a commute time of zero minutes, the index score is predicted to be (Round to three decimal places as needed.) O D. For every unit increase in index score, the commute time falls by , on average. (Round to three decimal places as needed.) O E. It is not appropriate to interpret the y-intercept because a commute time of zero minutes does not make sense and the value of zero minutes is much smaller than those observed in the data set. (c) Predict the well-being index of a person whose commute time is 30 minutes. The predicted index score is. (Round to one decimal place as needed.) (d) Suppose Barbara has a 15-minute commute and scores 67.3 on the survey. Is Barbara more "well-off" than the typical individual who has a 15-minute commute? Select the correct choice below and fill in the answer box to complete your choice. (Round to one decimal place as needed.) O A. Yes, Barbara is more well-off because the typical individual who has a 15-minute commute scores O B. No, Barbara is less well-off because the typical individual who has a 15-minute commute scores Time Remaining: 02:05:25 Next MacBook Air A 44 DII DD F9 F10 Q F7 F6 F3al Exam Question 11 of 20 This test: 150 point(s) possible This question: 10 point(s) possible Submit test list K Conduct a test at the a = 0.10 level of significance by determining (a) the null and alternative hypotheses, (b) the test statistic, and (c) the P-value. Assume the samples were obtained independently from a large population using simple random sampling. Test whether P1 > P2. The sample data are x1 = 129, n, = 256, X2 = 138, and n2 = 304. (a) Choose the correct null and alternative hypotheses below. O A. Ho: P1 = P2 Versus H1 : P1 # P2 O B. Ho: P1 = P2 versus H1: P1 P2 (b) Determine the test statistic. Zo = (Round to two decimal places as needed.) (c) Determine the P-value. The P-value is 10 (Round to three decimal places as needed.) What is the result of this hypothesis test? 11 O A. Do not reject the null hypothesis because there is not sufficient evidence to conclude that p, > P2. O B. Do not reject the null hypothesis because there is not sufficient evidence to conclude that p1 # P2. 1 12 O C. Do not reject the null hypothesis because there is not sufficient evidence to conclude that p1 H2 at the a = 0.10 level of significance for the given sample data. n 23 25 (b) Construct a 99% confidence interval about 1 - H2- 51.2 42.2 6.9 13.3 OA. HO: H1 = H2 OB. HO: My

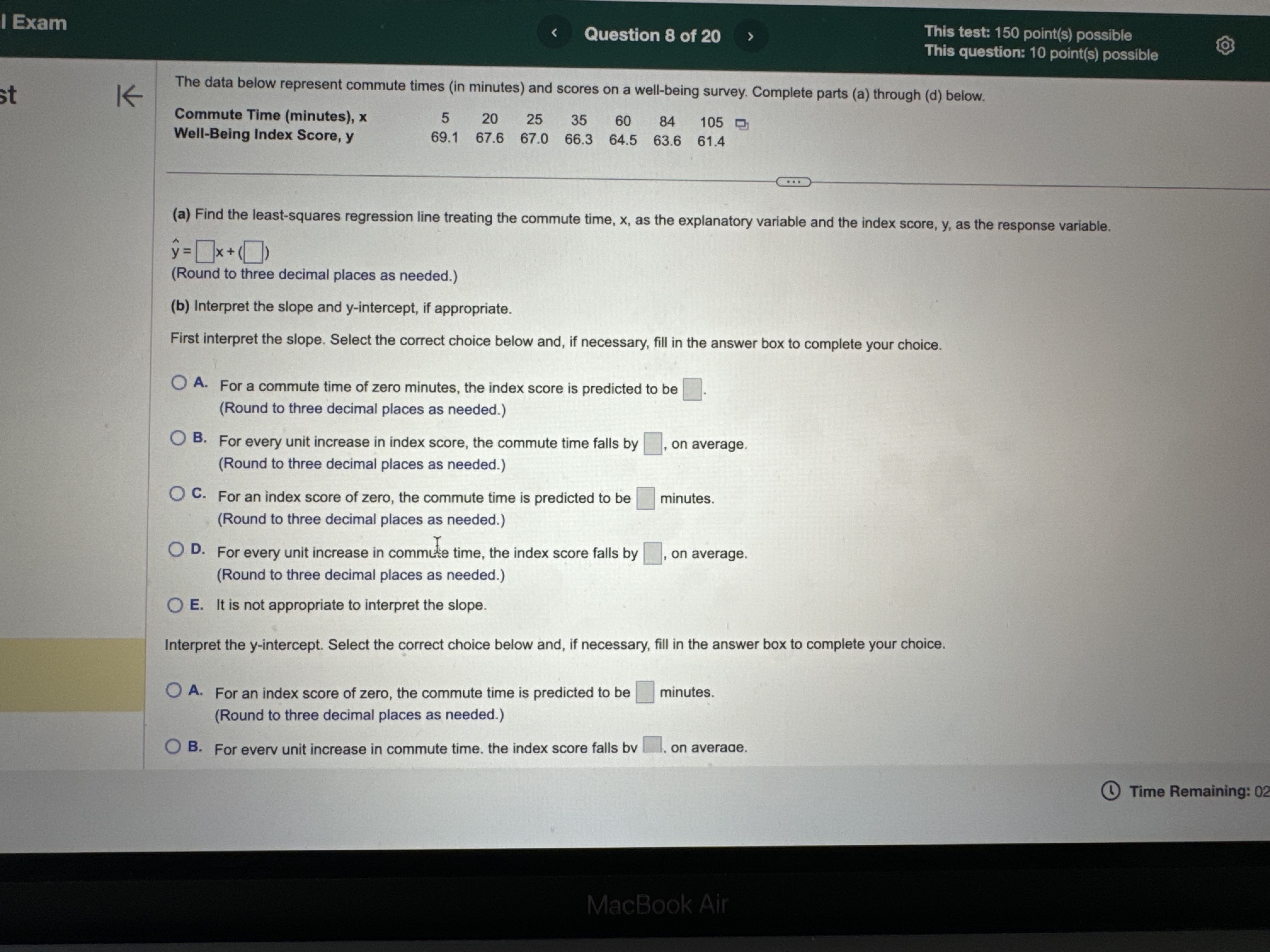
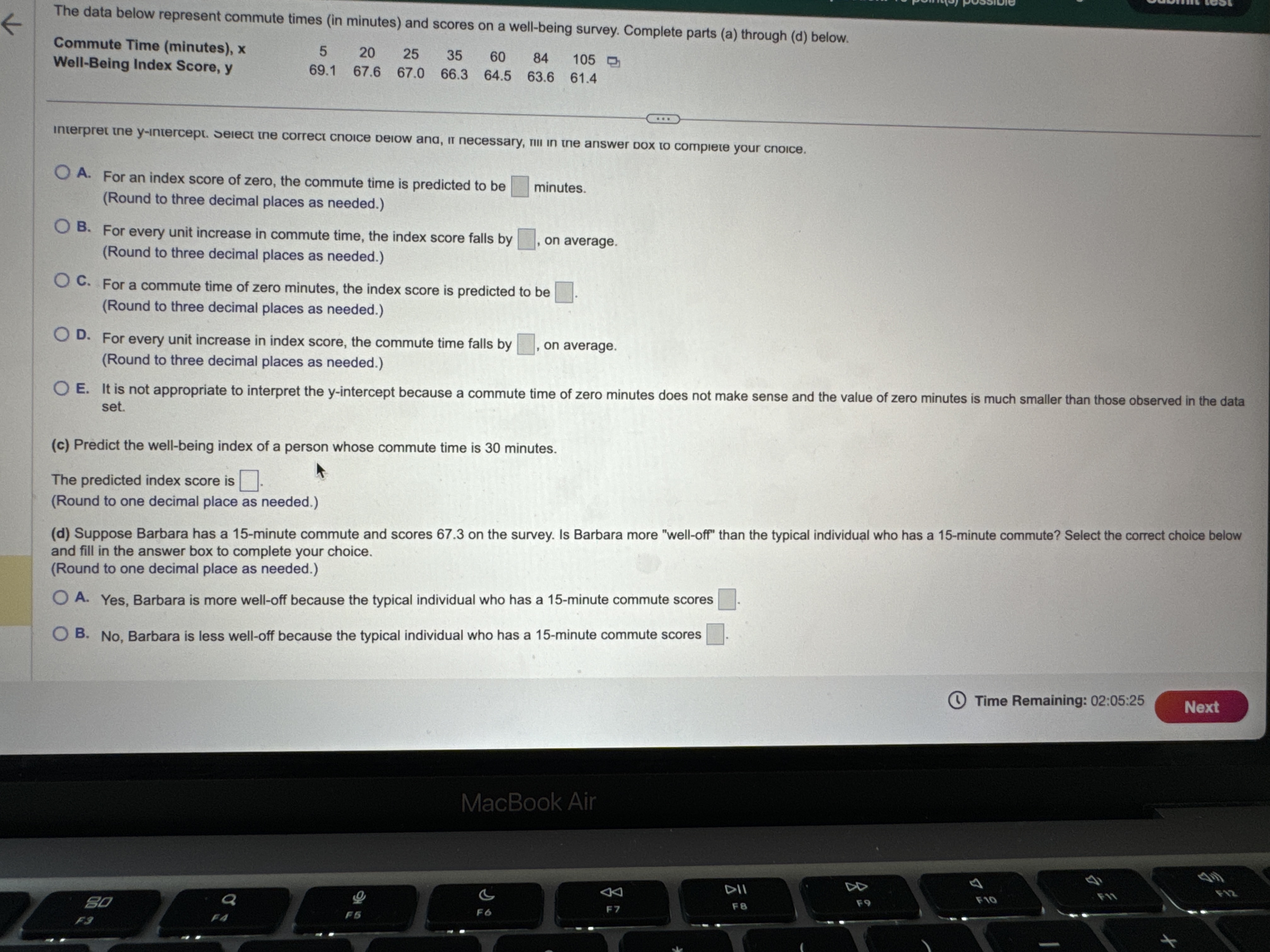
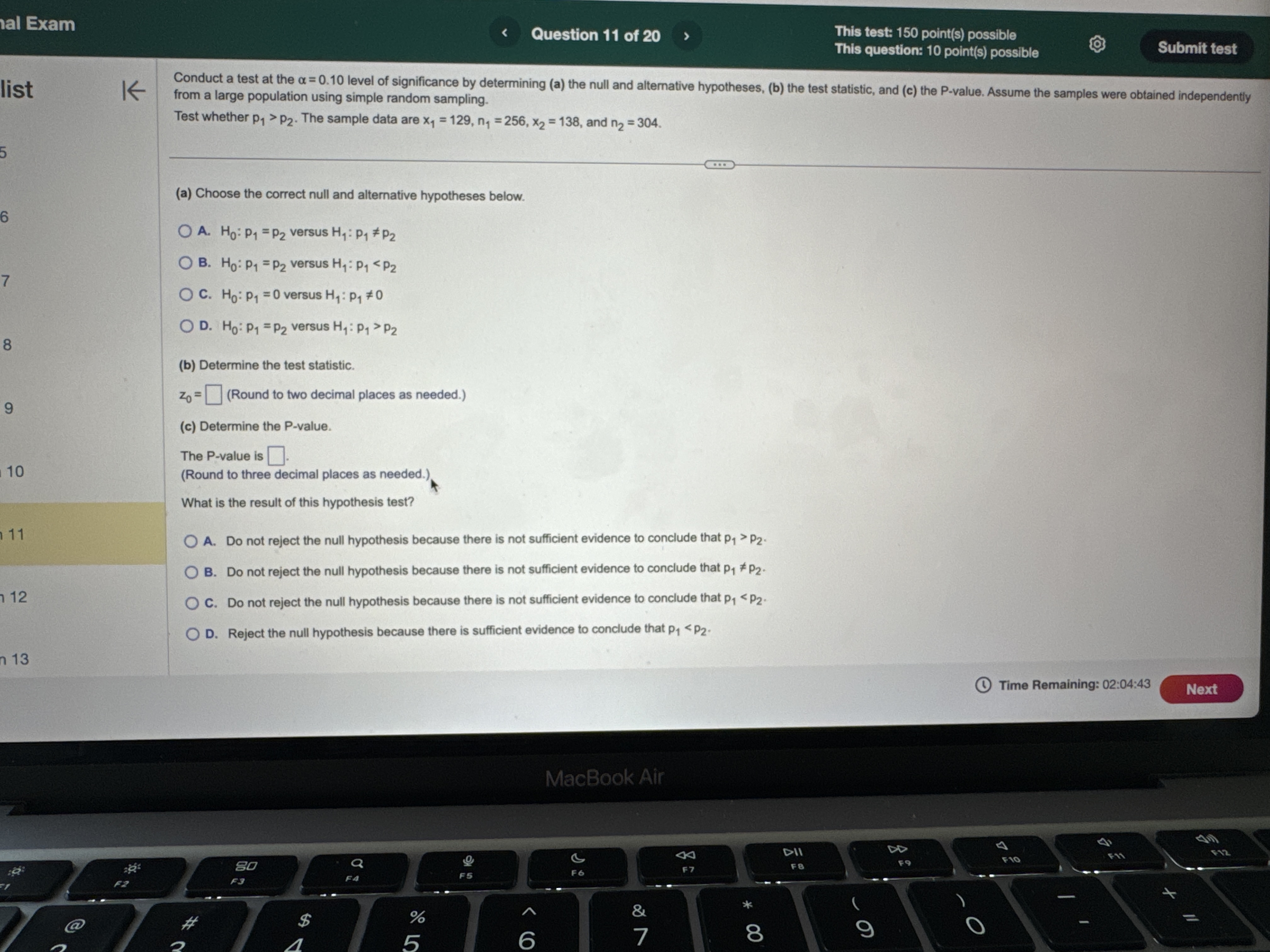
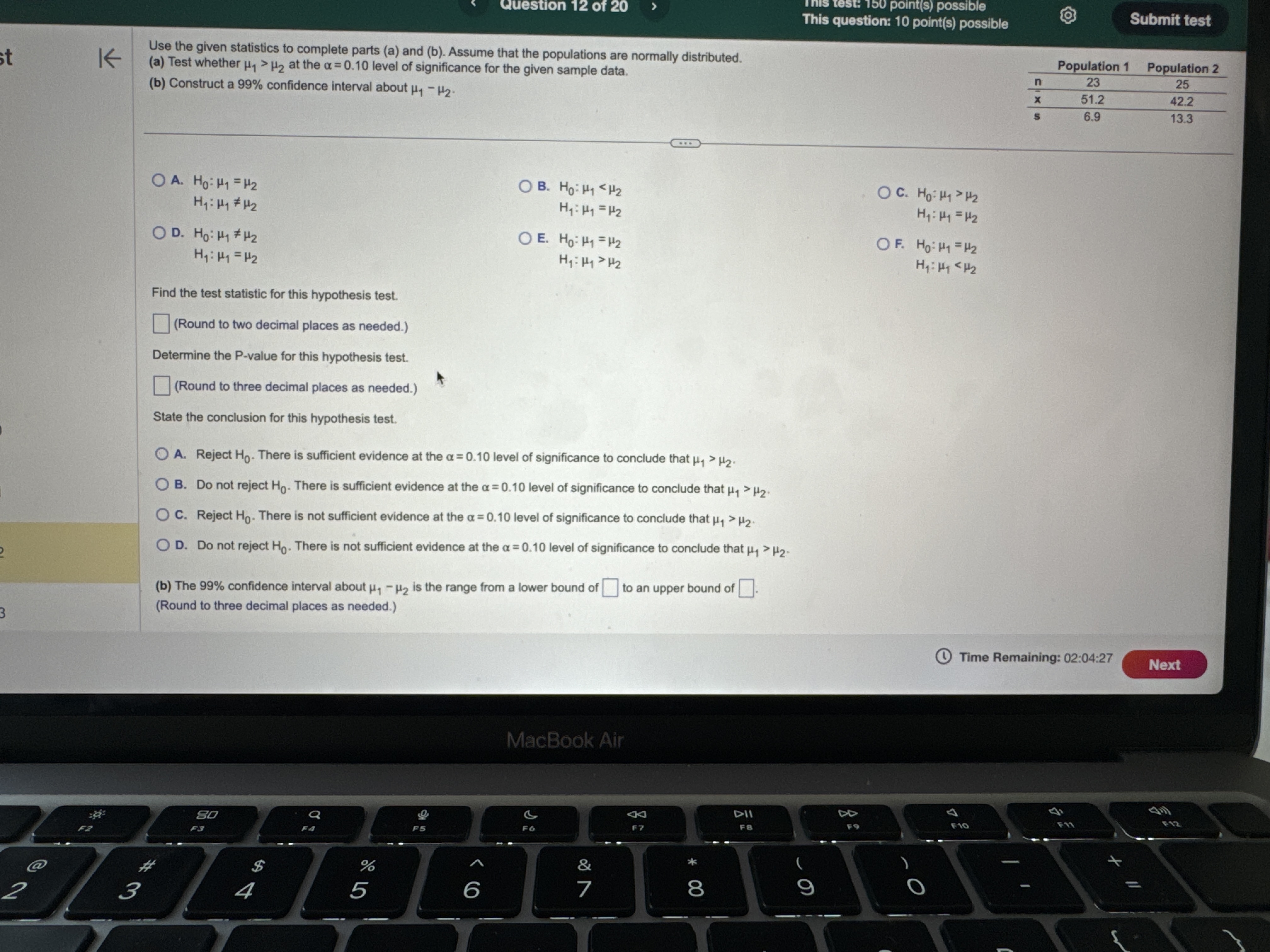
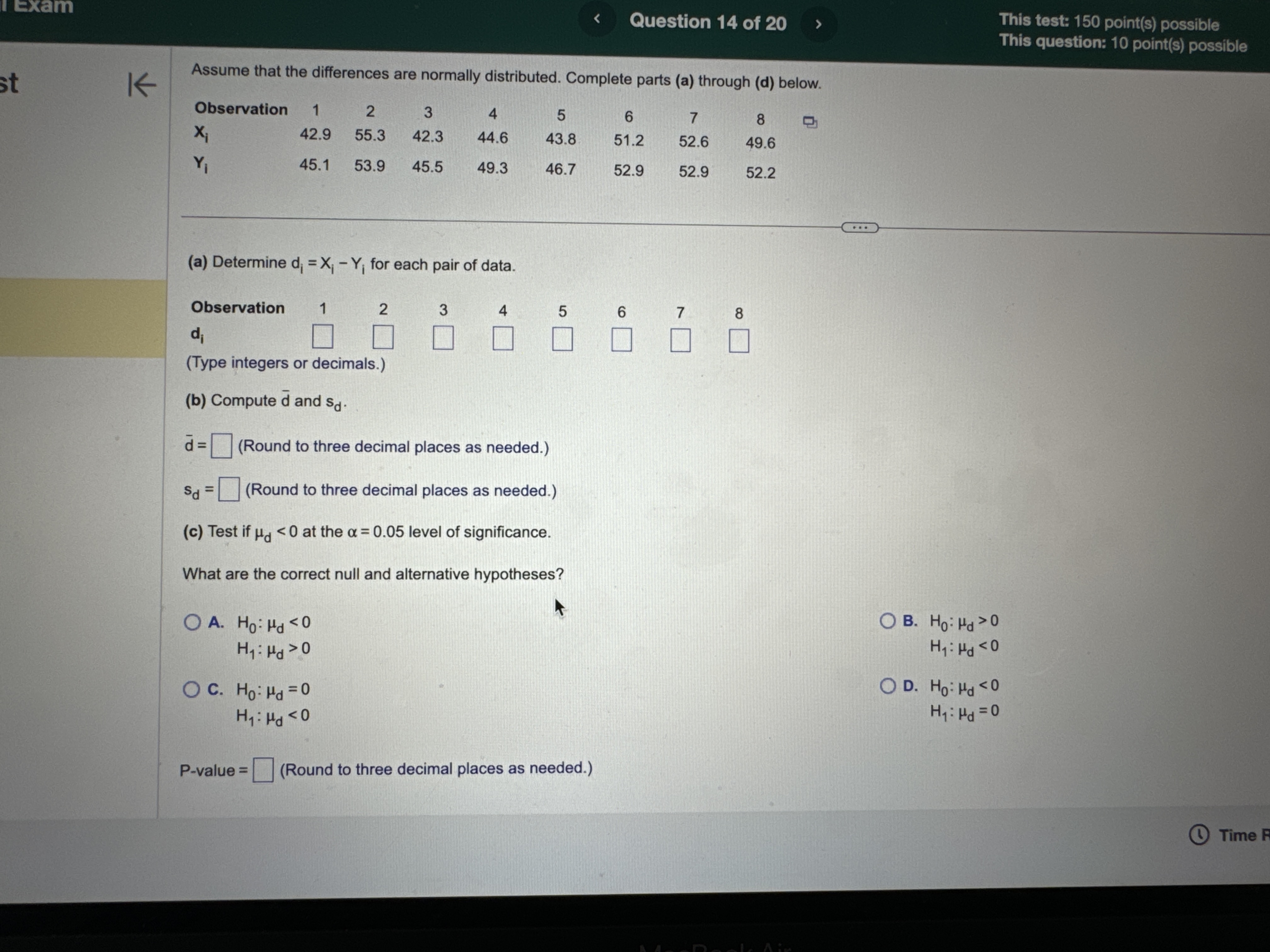
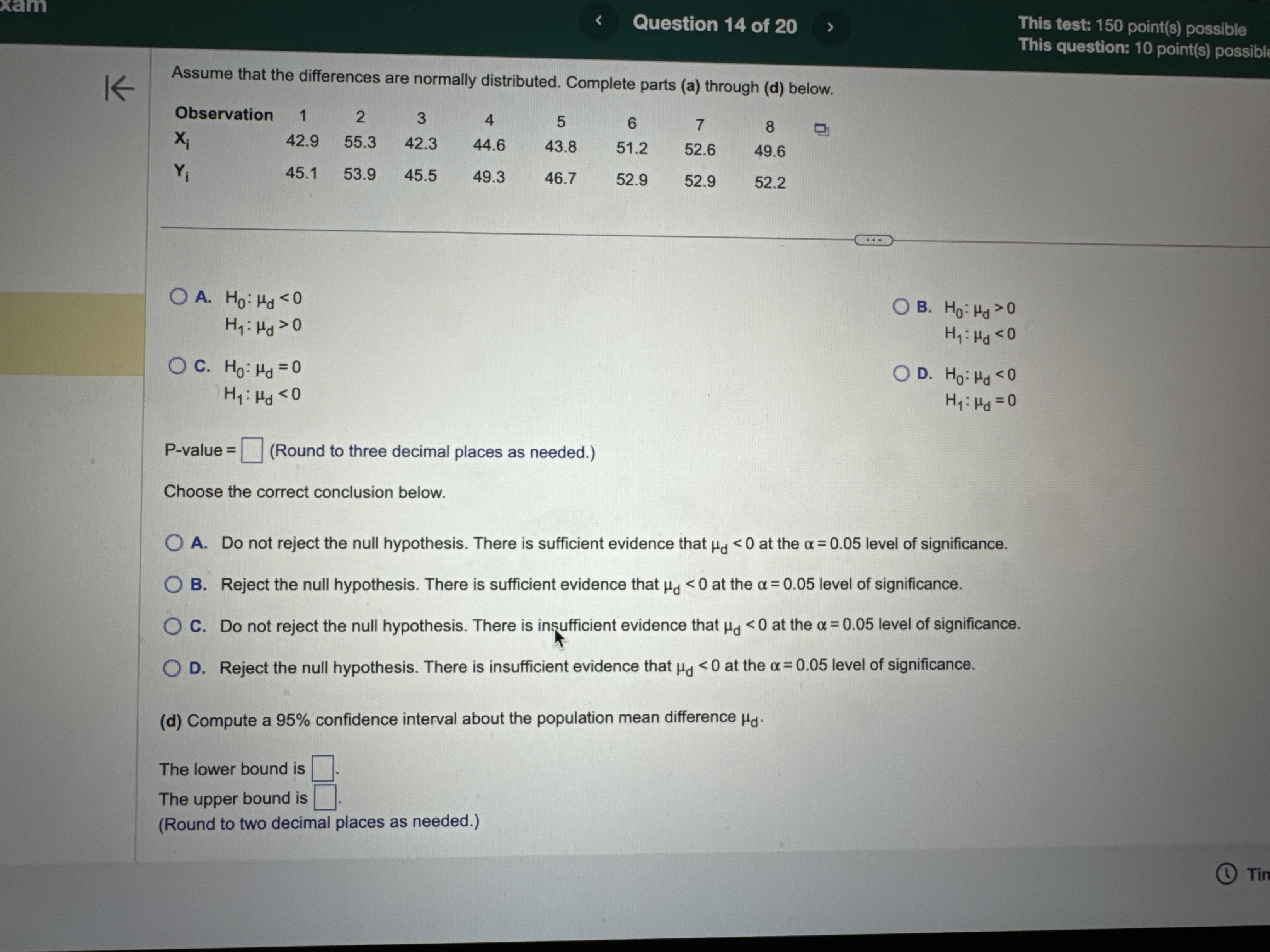
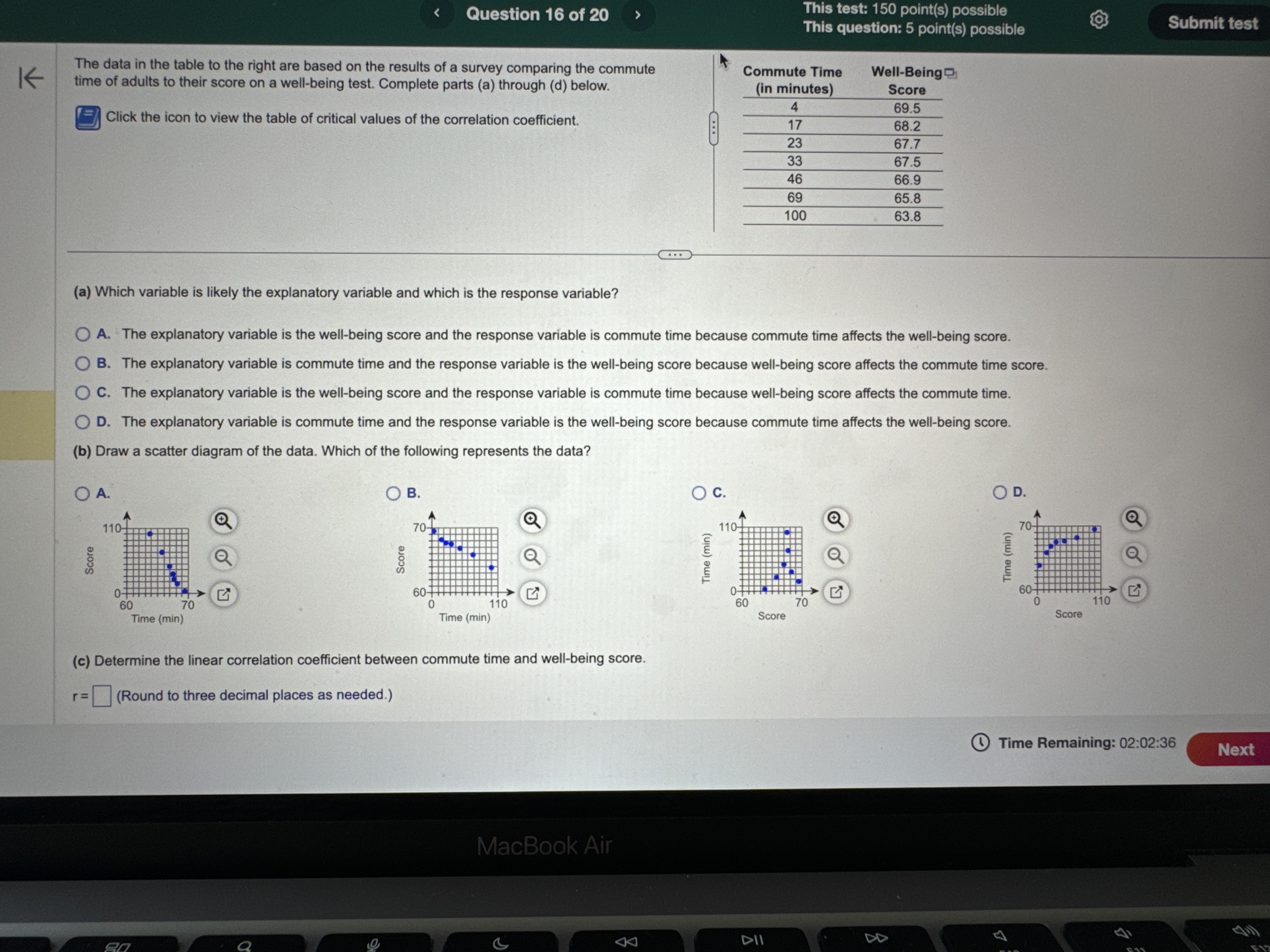
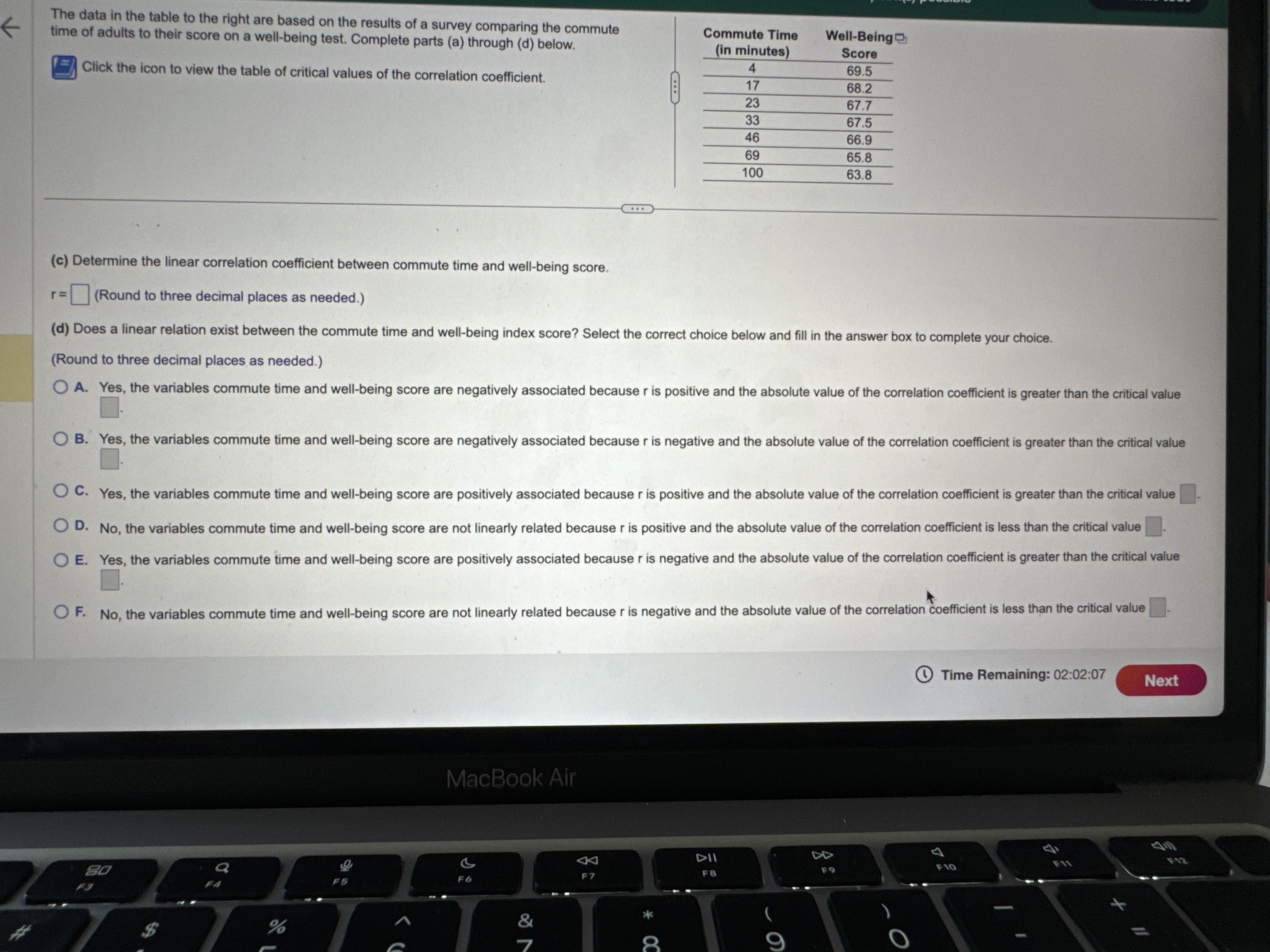
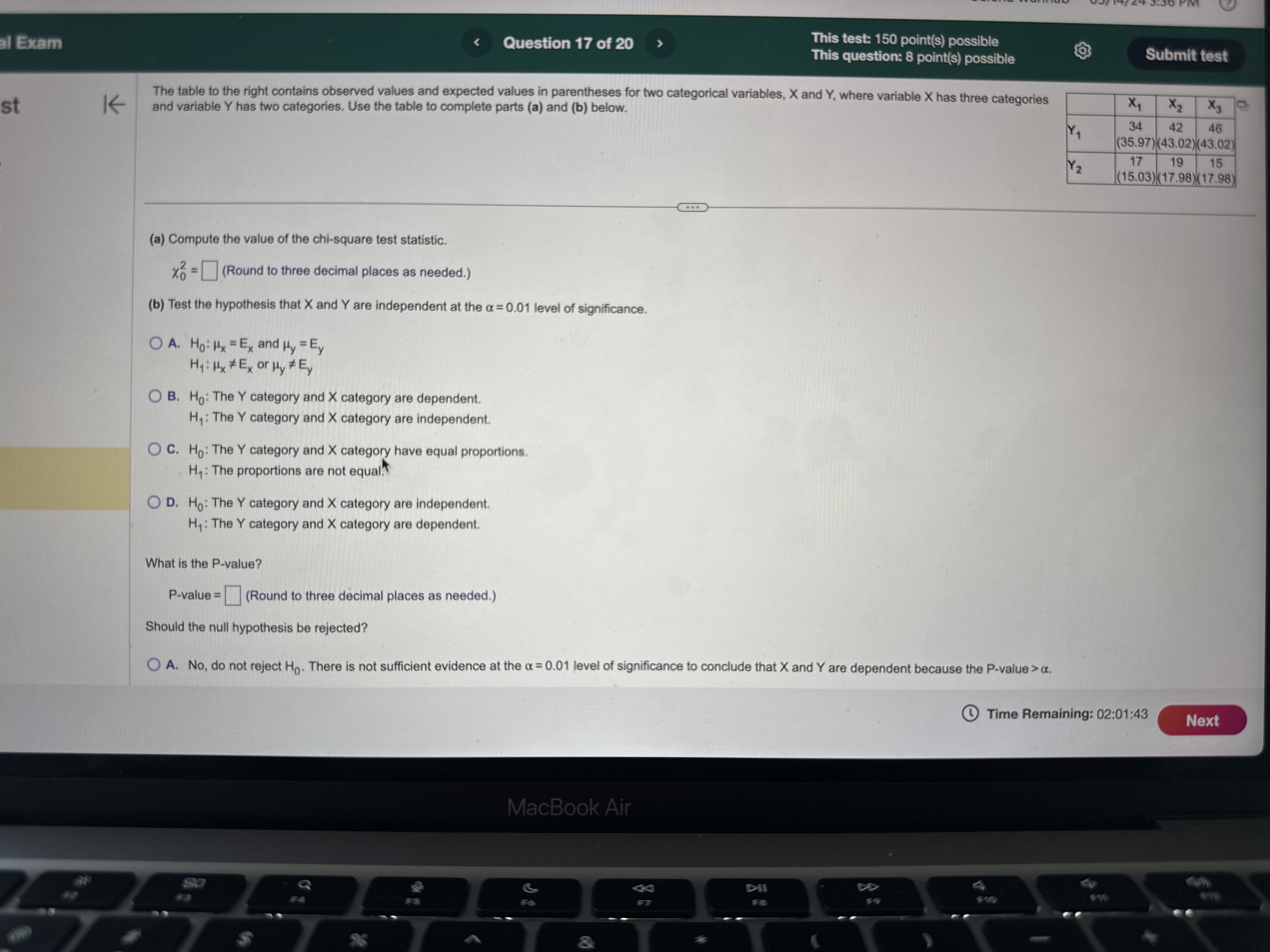
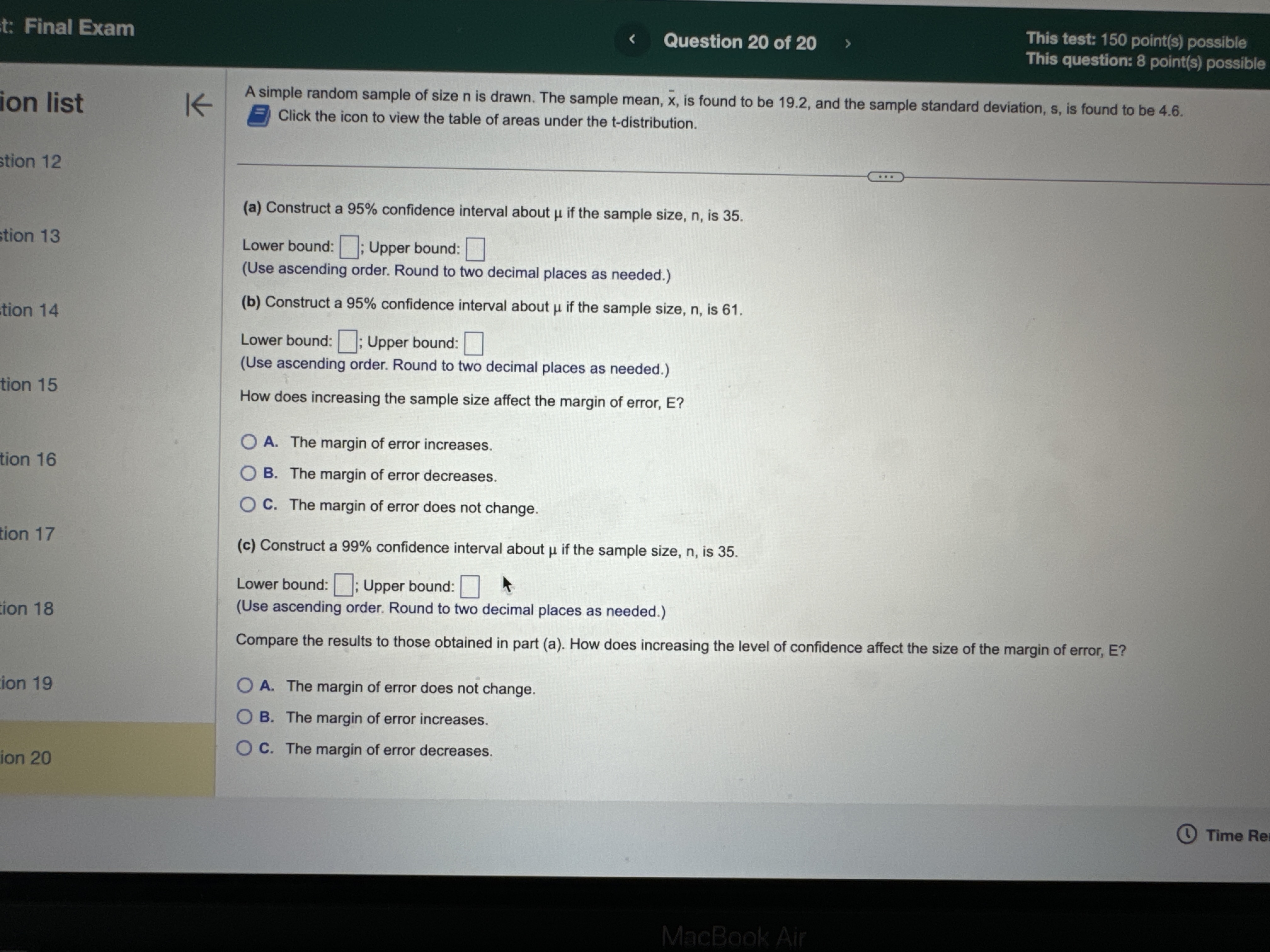
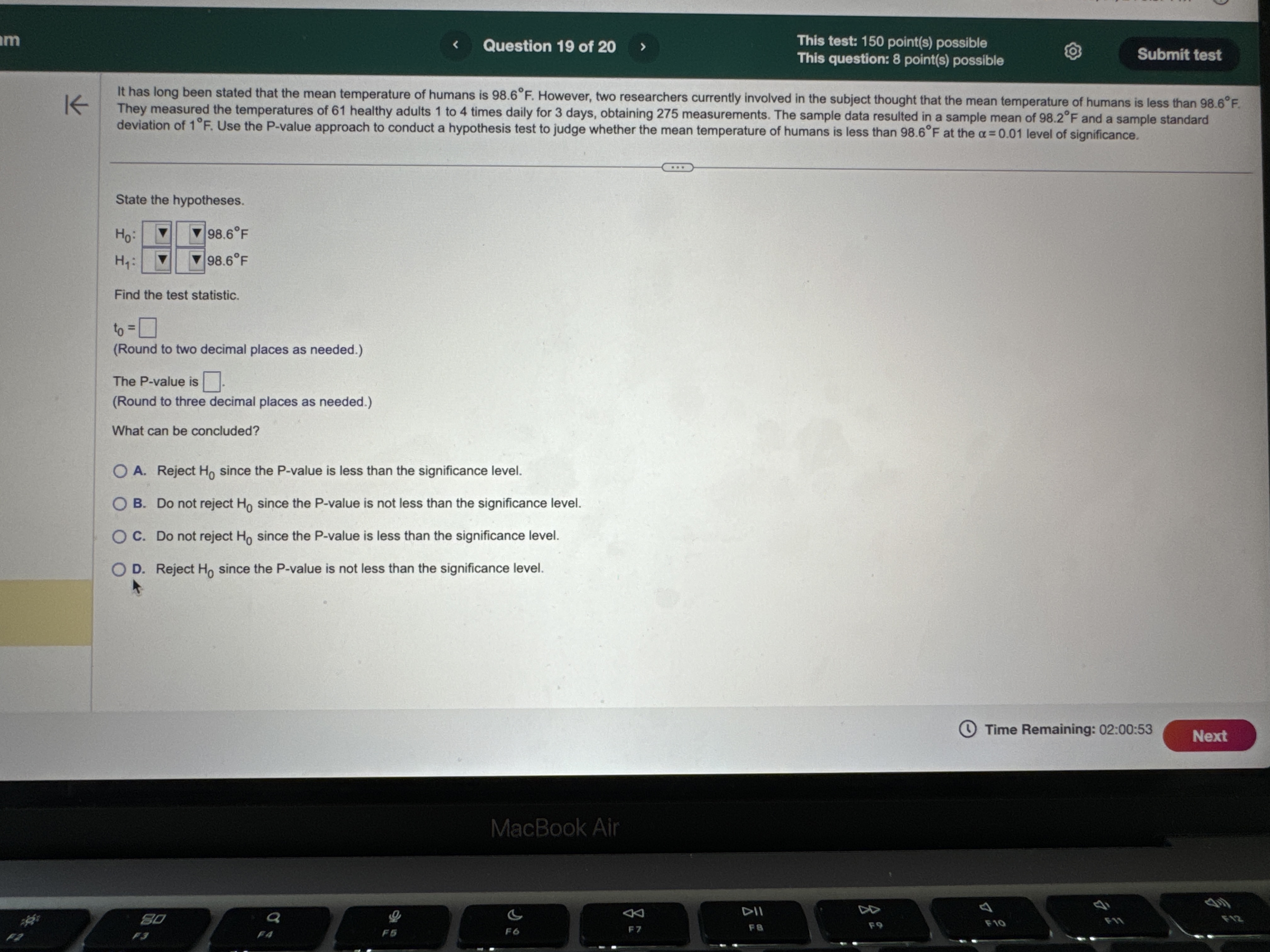
H2 Hy : Hy # H 2 Hy : My = H2 Hy: My = H2 OD. HO: My # H2 OE. HO: H1 = H2 OF. HO: Hy = H2 Hy: 141 = H2 H1 : 14 > H2 Hy: Hy

H2 O B. Do not reject Ho. There is sufficient evidence at the a = 0.10 level of significance to conclude that #1 > H2- O C. Reject Ho. There is not sufficient evidence at the a = 0.10 level of significance to conclude that #1 > H2. O D. Do not reject Ho. There is not sufficient evidence at the a = 0.10 level of significance to conclude that #1 > H2- (b) The 99% confidence interval about , - H2 is the range from a lower bound of to an upper bound of ]. (Round to three decimal places as needed.) Time Remaining: 02:04:27 Next MacBook Air A 44 F10 F11 80 S FO F7 FA @ % O 4 5 6 8 9Exam Question 14 of 20 This test: 150 point(s) possible This question: 10 point(s) possible Assume that the differences are normally distributed. Complete parts (a) through (d) below. st K Observation 1 2 3 5 6 8 X 42.9 55.3 42.3 44.6 43.8 51.2 52.6 49.6 45.1 53.9 45.5 49.3 46.7 52.9 52.9 52.2 (a) Determine di = X; - Y; for each pair of data. Observation di (Type integers or decimals.) (b) Compute d and sd. d = (Round to three decimal places as needed.) Sd = (Round to three decimal places as needed.) (c) Test if Ha 0 OA. Ho: Hd 0 OD. Ho: Hd 0 Hy : H d > 0 Hy : Hd a. ) 0 P i @ Time Remaining: 02:01:43 m i t: Final Exam Question 20 of 20 This test: 150 point(s) possible This question: 8 point(s) possible ion list K A simple random sample of size n is drawn. The sample mean, x, is found to be 19.2, and the sample standard deviation, s, is found to be 4.6. Click the icon to view the table of areas under the t-distribution. stion 12 (a) Construct a 95% confidence interval about u if the sample size, n, is 35. tion 13 Lower bound: ; Upper bound: (Use ascending order. Round to two decimal places as needed.) tion 14 (b) Construct a 95% confidence interval about u if the sample size, n, is 61. Lower bound: ; Upper bound: (Use ascending order. Round to two decimal places as needed.) tion 15 How does increasing the sample size affect the margin of error, E? A. The margin of error increases. tion 16 O B. The margin of error decreases O C. The margin of error does not change. tion 17 (c) Construct a 99% confidence interval about u if the sample size, n, is 35. Lower bound: ; Upper bound: tion 18 (Use ascending order. Round to two decimal places as needed.) Compare the results to those obtained in part (a). How does increasing the level of confidence affect the size of the margin of error, E? ion 19 O A. The margin of error does not change. O B. The margin of error increases. ion 20 O C. The margin of error decreases. Time Re MacBook AirQuestion 19 of 20 This test: 150 point(s) possible @ This question: 8 point(s) possible S L It has long been stated that the mean temperature of humans is 98.6F. However, two researchers currently involved in the subject thought that the mean temperature of humans is less than 98 They mnsur?'d the temperatures of 61 healthy adults 1 to 4 times daily for 3 days, obtaining 275 measurements. The sample data resulted in a sample mean of 98.2F and a sample standard deviation of 1F. Use the P-value approach to conduct a hypothesis test to judge whether the mean temperature of humans is less than 98.6F at the a=0.01 level of significance. G2 State the hypotheses. Ho: 98.6F Hy: | ]| [v|os6F Find the test statistic. ' 6= | (Round to two decimal places as needed.) The P-valueis | |. (Round to three decimal places as needed.) What can be concluded? O A. Reject H,, since the P-value is less than the significance level O B. Do not reject Hy since the P-value is not less than the significance level C. Do not reject H, since the P-value is less than the significance level O D. Reject H, since the P-value is not less than the significance level [ & @ Time Remaining: 02:00:53 al Exam (S R This test: 150 point(s) possible @ Submit test This question: 8 point(s) possible | According to flightstats.com, American Airlines flights from Dallas to Chicago are on time 80% of the time. Su i imber of on-time recorded. . | G sta m, ppose 17 flights are randomly selected, and the n flights |st le { (a) Explain why this is a binomial experiment. g d e o > 4 | (b) Determine the values of n and p. () Find and interpret the probability that exactly 11 flights are on time 2 (d) Find and interpret the probability that at least 11 flights are on time e = 3 = L F. Each tnal depends on the previous trial e G. The experiment is performed until a desired number of successes are reached 4 H. The experiment is performed a fixed number of times (b) Using the binomial distribution, determine the values of n and p. 5 n= (Type an integer or a decimal. Do not round.) p=