Algorithm and Complexity, Python

Task 1

def binary_search(numbers, x_number):

low_index = 0

high_index = len(numbers) - 1

while low_index

middle_index = low_index + (high_index - low_index) // 2

if x_number

high_index = middle_index - 1

elif x_number > numbers[middle_index]:

low_index = middle_index + 1

else:

return True;

return False

a. Test the above function for some lists and values of x_number. b. Show that the complexity of the best (most favorable) case is O(1). Precisely when this can happen c. Write a naive program to check the presence of x_number in the list numbers comparing consecutive elements of the list with x_number. What is the complexity of the algorithm implemented this way? d. Using several examples, show that the number of operations performed by the naive program is larger than that of the binary_search.

e. Appropriately change the following piece of code to get an estimation of the time needed by your system to perform a search with two methods.

import time

def sum_of_n_numbers(n):

start_time = time.time()

s = 0

for i in range(1,n+1):

s = s + i

end_time = time.time()

return s,end_time-start_time

n = 100000

print(" Time to sum of 1 to ",n," and required time to calculate is :",

sum_of_n_numbers(n))

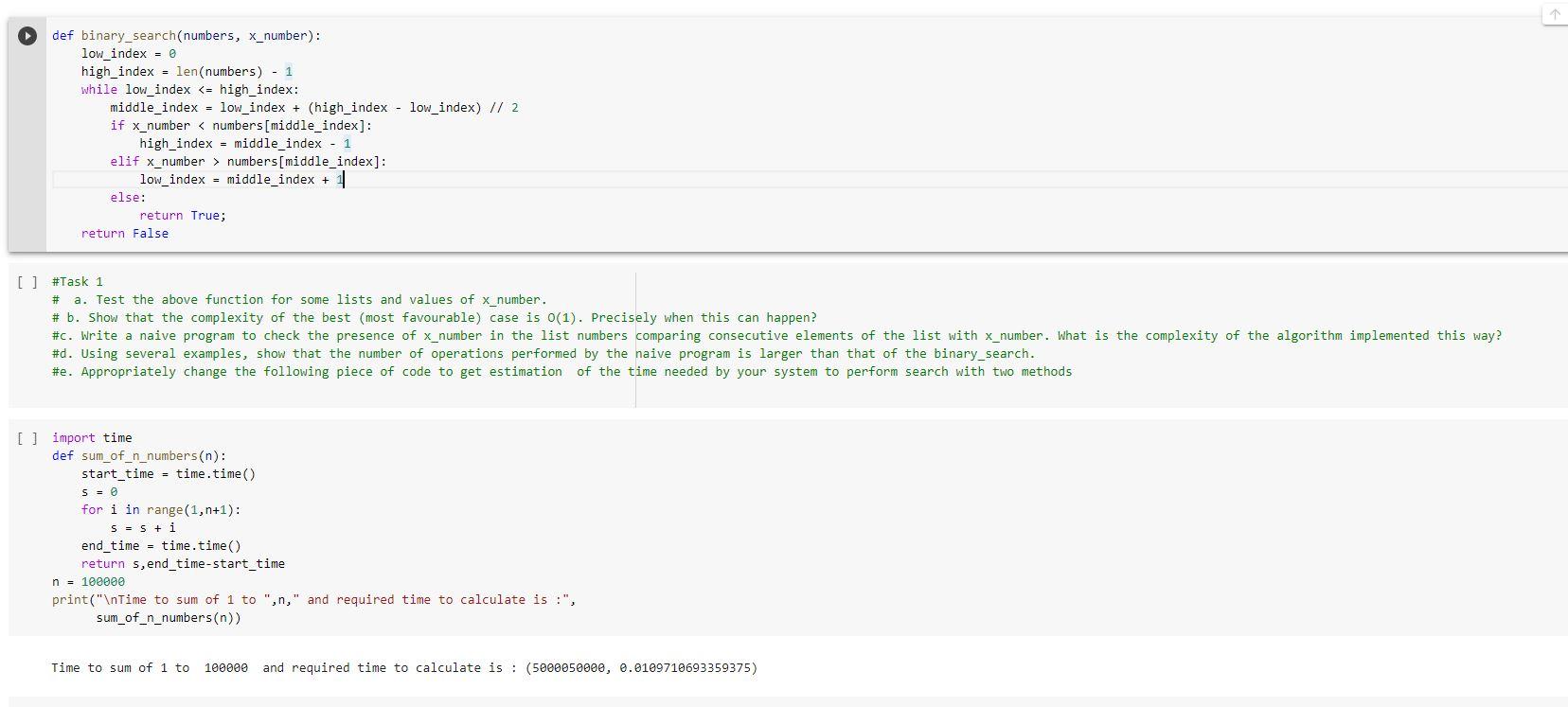
def binary_search(numbers, X_number): low_index - 0 high_index = len(numbers) - 1 while low_index numbers[middle_index]: low_index = middle_index + else: return True; return false [] #Task 1 # a. Test the above function for some lists and values of x_number. # b. Show that the complexity of the best (most favourable) case is 0(1). Precisely when this can happen? #c. Write a naive program to check the presence of x_number in the list numbers comparing consecutive elements of the list with x_number. What is the complexity of the algorithm implemented this way? #d. Using several examples, show that the number of operations performed by the naive program is larger than that of the binary_search. #e. Appropriately change the following piece of code to get estimation of the time needed by your system to perform search with two methods [] import time def sum_of_n_numbers(n): start_time = time.time() S = for i in range(1, n+1): S = S + i end_time = time.time) return s, end_time-start_time n = 10000e print(" Time to sum of 1 to ",n," and required time to calculate is :", sum_of_n_numbers(n)) Time to sum of 1 to 100000 and required time to calculate is : (5000050000, 0.0199710693359375)