ALGORITHMS/ DIRECTED MULTIGRAPHS QUESTION:

The goal of this question is to find a way to efficiently convert directed multigraphs into undirected simple graphs.

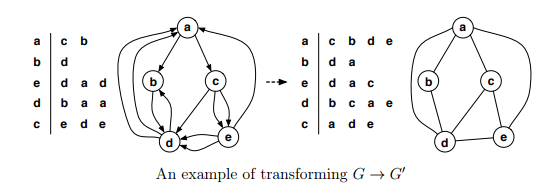
Let G = (E, V ) denote a directed multigraph. An undirected simple graph is a G0= (V, E0 ), such that E 0 is derived from the edges in E so that (i) every directed multi-edge, e.g., {(u, v),(u, v)} or even simply {(u, v)}, has been replaced by a single pair of directed edges {(u, v),(v, u)} and (ii) all self-loops (u, u) have been removed.

Describe and analyze an algorithm (explain how it works, give pseudocode if necessary, derive its running time and space usage, and prove its correctness) that takes O(V + E) time and space to convert G into G0 , and thereby will solve any arbitrary instance of this problem. Assume both G and G0 are stored as adjacency lists. Hints: Dont assume adjacencies Adj[u] are ordered in any particular way and remember that you can add edges to the list and then remove ones you dont need.

a c b d e Ro ed a c Itia G3 An example of transforming G G, a c b d e Ro ed a c Itia G3 An example of transforming G G