All given information is provided in screenshots. The file "main.py" is provided in screenshot as well. No need to download nor upload it. Thank you

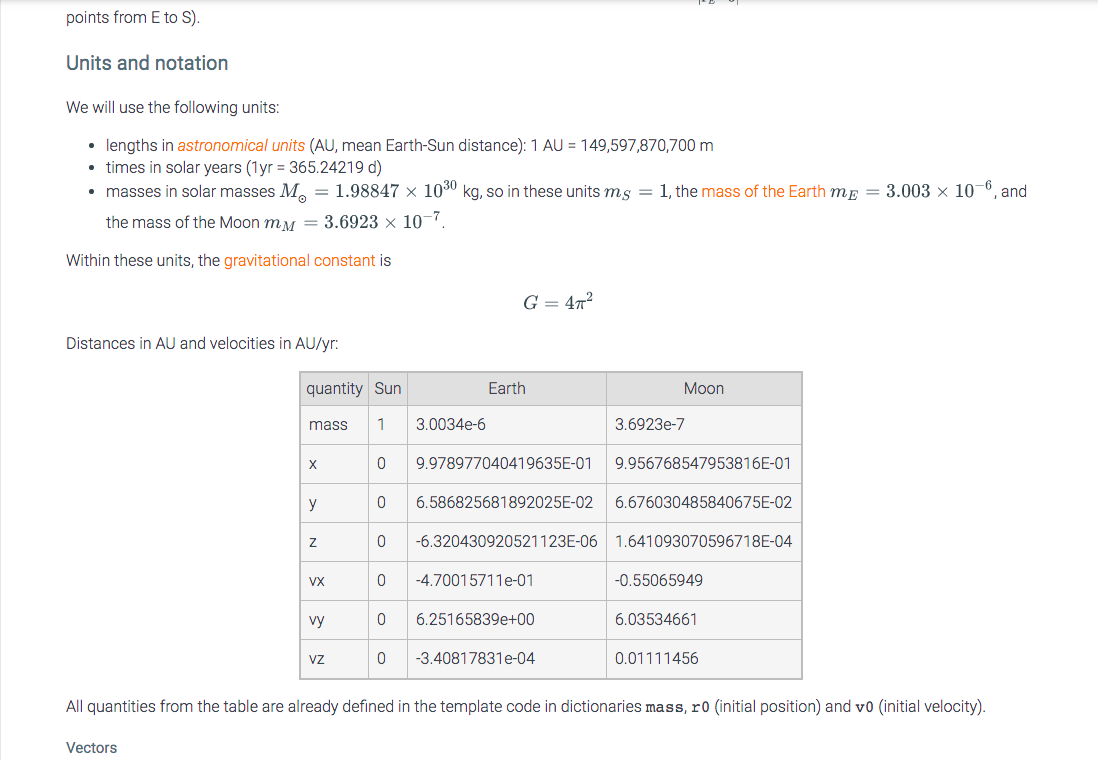


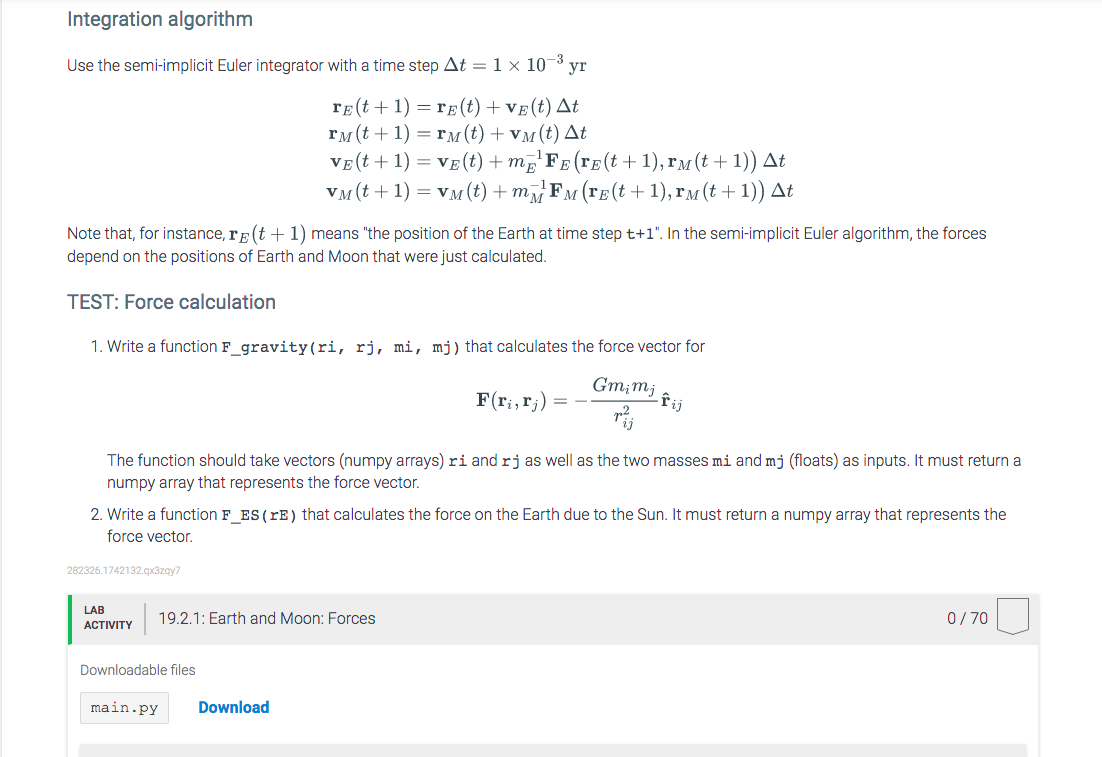
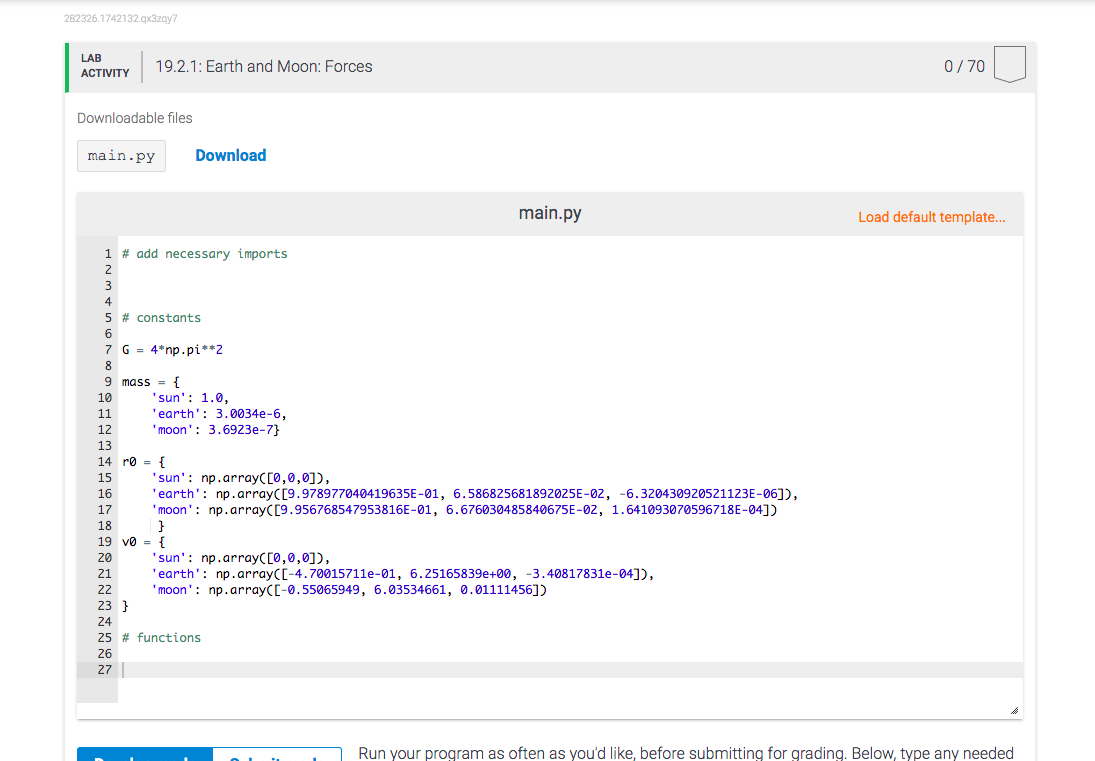
The goal of this project is to simulate the trajectories of the Earth and the Moon during one year. You are given the initial positions and velocities and masses. Because the mass of the Sun is so much bigger than those of Earth and Moon, we can consider the Sun fixed at the origin of our coordinate system and you only have to calculate the trajectories of Earth and Moon. The problem is broken down into four smaller zyLabs. Most of the background and theory is written down in this zyLab, though, and you can come back to this problem when you are working on later zyLabs. However, in this zyLab you will only have to calculate forces. You will then use your force calculations in subsequent zyLabs (copy & paste your own code). Newton's law of gravity The bodies interact via Newton's law of gravity. The force depends on the distance between the two bodies with an inverse square law and the masses of the bodies. Specifically, the force on body i at position r; due to body j at position r; is Fij = F(ri, r;) = F(rij) = Gmim; fij rij:=r; - rj rij fij:= Tij T'ij = rijl = V rij rij The two bodies have masses mi and m; and G is the gravitational constant. The vector fij is the unit vector pointing from body i towards body i. For example, if we want to calculate the force on the Earth E due to the Sun S where rs = 0 = (0,0,0) (because the Sun is fixed at the origin) we get FES(re) Gmems fE re-o re-0 i.e., the force on the Earth always points towards the Sun (because the unit vector E ES points from E to S). fe points from Sto E and so- points from E to S) Units and notation We will use the following units: lengths in astronomical units (AU, mean Earth-Sun distance): 1 AU = 149,597,870,700 m times in solar years (1yr = 365.24219 d) masses in solar masses M. = 1.98847 x 1030 kg, so in these units ms = 1, the mass of the Earth me = 3.003 x 10-6, and the mass of the Moon mm = 3.6923 x 10-7. Within these units, the gravitational constant is G = 472 Distances in AU and velocities in AU/yr: quantity Sun Earth Moon mass 1 3.0034e-6 3.6923e-7 0 9.978977040419635E-01 9.956768547953816E-01 0 6.586825681892025E-02 6.676030485840675E-02 z 0 -6.320430920521123E-06 1.641093070596718E-04 VX 0 -4.70015711e-01 -0.55065949 vy 0 6.25165839e+00 6.03534661 VZ 0 -3.40817831e-04 0.01111456 All quantities from the table are already defined in the template code in dictionaries mass, ro (initial position) and vo initial velocity). Vectors Vectors Reminder of vector algebra and calculus: A Cartesian vector in 3D consists of three components 2 r = - y Difference vector: 2-2j rij = ri - r;= Yi - y 2; aj Inner product: 3 a. b = x2 + ya Yu + 2a 2b = a=1 r:r = x2 + y2 + 22 - Derivatives: dac dr(t) dt = v(t) dz dt | | dt dr(t) = a(t) dt2 dt? Equations of motions Equations of motions The equations of motions for Earth r(t) and Moon rm(t): dre = ma me Fe(t) dt2 drm = m Fm(t) dt2 mi F1 where the total force on the Earth consists of the force from the Sun on the Earth and the force of the Moon on the Earth: FE(t) = FES(t) + FEM(t) Similarly, the force on the Moon FM(t) = Fms(t) + FME(t) is exerted by the Sun and the Earth. The force from the Moon on the Earth is GEM EM(t) FEM(t) p M (t) and the force from the Earth on the Moon is FME(t) FEM(t) (Newton's 3rd law). Integration algorithm Use the semi-implicit Euler integrator with a time step At = 1 x 10-3 yr re(t + 1) =re(t) + ve(t) At + A+ Integration algorithm Use the semi-implicit Euler integrator with a time step At = 1 x 10-3, yr re(t+1) = re(t) + ve(t) At rm(t+1) = rm(t) + vm(t) At ve(t+1) = ve(t) +me'Fe(re(t+1), rm(t+1)) At vm(t+1) = vm(t) +m7 Fm(re(t+1),rm(t + 1)) At Note that, for instance, re(t+1) means "the position of the Earth at time step t+1". In the semi-implicit Euler algorithm, the forces depend on the positions of Earth and Moon that were just calculated. TEST: Force calculation 1. Write a function F_gravity(ri, rj, mi, mj) that calculates the force vector for F(ri, r;) Gmimi -fij The function should take vectors (numpy arrays) ri and rj as well as the two masses mi and mj (floats) as inputs. It must return a numpy array that represents the force vector. 2. Write a function F_ES (VE) that calculates the force on the Earth due to the Sun. It must return a numpy array that represents the force vector 282326.1742132.qx3zqy7 LAB ACTIVITY 0/70 19.2.1: Earth and Moon: Forces Downloadable files main.py Download 282326. 1742132.qx3zay? LAB ACTIVITY 19.2.1: Earth and Moon: Forces 0/70 Downloadable files main.py Download main.py Load default template... 1 # add necessary imports 2 3 5 # constants 7 G = 4*np.pi**2 9 mass = { 'sun': 1.0, earth': 3.0034e-6, 'moon' : 3.6923e-7} 14 r0 = { 15 15 'sun': np.array([0,0,0]), 16 16 earth': np.array([9.978977048419635E-01, 6.586825681892025E-02, -6.320430920521123E-06]), 17 17 'moon': np.array([9.956768547953816E-01, 6.676030485840675E-02, 1.641093070596718E-84]) 18 18 } 19 v0 = { 20 'sun': np.array([0,0,0]), 40 21 earth': np.array([-4.70015711e-01, 6.25165839e+00, -3.40817831e-04]), 22 'moon': np.arrayC[-0.55065949, 6.03534661, 0.01111456]) 23 } 24 25 # functions 26 27 Run your program as often as you'd like, before submitting for grading. Below, type any needed The goal of this project is to simulate the trajectories of the Earth and the Moon during one year. You are given the initial positions and velocities and masses. Because the mass of the Sun is so much bigger than those of Earth and Moon, we can consider the Sun fixed at the origin of our coordinate system and you only have to calculate the trajectories of Earth and Moon. The problem is broken down into four smaller zyLabs. Most of the background and theory is written down in this zyLab, though, and you can come back to this problem when you are working on later zyLabs. However, in this zyLab you will only have to calculate forces. You will then use your force calculations in subsequent zyLabs (copy & paste your own code). Newton's law of gravity The bodies interact via Newton's law of gravity. The force depends on the distance between the two bodies with an inverse square law and the masses of the bodies. Specifically, the force on body i at position r; due to body j at position r; is Fij = F(ri, r;) = F(rij) = Gmim; fij rij:=r; - rj rij fij:= Tij T'ij = rijl = V rij rij The two bodies have masses mi and m; and G is the gravitational constant. The vector fij is the unit vector pointing from body i towards body i. For example, if we want to calculate the force on the Earth E due to the Sun S where rs = 0 = (0,0,0) (because the Sun is fixed at the origin) we get FES(re) Gmems fE re-o re-0 i.e., the force on the Earth always points towards the Sun (because the unit vector E ES points from E to S). fe points from Sto E and so- points from E to S) Units and notation We will use the following units: lengths in astronomical units (AU, mean Earth-Sun distance): 1 AU = 149,597,870,700 m times in solar years (1yr = 365.24219 d) masses in solar masses M. = 1.98847 x 1030 kg, so in these units ms = 1, the mass of the Earth me = 3.003 x 10-6, and the mass of the Moon mm = 3.6923 x 10-7. Within these units, the gravitational constant is G = 472 Distances in AU and velocities in AU/yr: quantity Sun Earth Moon mass 1 3.0034e-6 3.6923e-7 0 9.978977040419635E-01 9.956768547953816E-01 0 6.586825681892025E-02 6.676030485840675E-02 z 0 -6.320430920521123E-06 1.641093070596718E-04 VX 0 -4.70015711e-01 -0.55065949 vy 0 6.25165839e+00 6.03534661 VZ 0 -3.40817831e-04 0.01111456 All quantities from the table are already defined in the template code in dictionaries mass, ro (initial position) and vo initial velocity). Vectors Vectors Reminder of vector algebra and calculus: A Cartesian vector in 3D consists of three components 2 r = - y Difference vector: 2-2j rij = ri - r;= Yi - y 2; aj Inner product: 3 a. b = x2 + ya Yu + 2a 2b = a=1 r:r = x2 + y2 + 22 - Derivatives: dac dr(t) dt = v(t) dz dt | | dt dr(t) = a(t) dt2 dt? Equations of motions Equations of motions The equations of motions for Earth r(t) and Moon rm(t): dre = ma me Fe(t) dt2 drm = m Fm(t) dt2 mi F1 where the total force on the Earth consists of the force from the Sun on the Earth and the force of the Moon on the Earth: FE(t) = FES(t) + FEM(t) Similarly, the force on the Moon FM(t) = Fms(t) + FME(t) is exerted by the Sun and the Earth. The force from the Moon on the Earth is GEM EM(t) FEM(t) p M (t) and the force from the Earth on the Moon is FME(t) FEM(t) (Newton's 3rd law). Integration algorithm Use the semi-implicit Euler integrator with a time step At = 1 x 10-3 yr re(t + 1) =re(t) + ve(t) At + A+ Integration algorithm Use the semi-implicit Euler integrator with a time step At = 1 x 10-3, yr re(t+1) = re(t) + ve(t) At rm(t+1) = rm(t) + vm(t) At ve(t+1) = ve(t) +me'Fe(re(t+1), rm(t+1)) At vm(t+1) = vm(t) +m7 Fm(re(t+1),rm(t + 1)) At Note that, for instance, re(t+1) means "the position of the Earth at time step t+1". In the semi-implicit Euler algorithm, the forces depend on the positions of Earth and Moon that were just calculated. TEST: Force calculation 1. Write a function F_gravity(ri, rj, mi, mj) that calculates the force vector for F(ri, r;) Gmimi -fij The function should take vectors (numpy arrays) ri and rj as well as the two masses mi and mj (floats) as inputs. It must return a numpy array that represents the force vector. 2. Write a function F_ES (VE) that calculates the force on the Earth due to the Sun. It must return a numpy array that represents the force vector 282326.1742132.qx3zqy7 LAB ACTIVITY 0/70 19.2.1: Earth and Moon: Forces Downloadable files main.py Download 282326. 1742132.qx3zay? LAB ACTIVITY 19.2.1: Earth and Moon: Forces 0/70 Downloadable files main.py Download main.py Load default template... 1 # add necessary imports 2 3 5 # constants 7 G = 4*np.pi**2 9 mass = { 'sun': 1.0, earth': 3.0034e-6, 'moon' : 3.6923e-7} 14 r0 = { 15 15 'sun': np.array([0,0,0]), 16 16 earth': np.array([9.978977048419635E-01, 6.586825681892025E-02, -6.320430920521123E-06]), 17 17 'moon': np.array([9.956768547953816E-01, 6.676030485840675E-02, 1.641093070596718E-84]) 18 18 } 19 v0 = { 20 'sun': np.array([0,0,0]), 40 21 earth': np.array([-4.70015711e-01, 6.25165839e+00, -3.40817831e-04]), 22 'moon': np.arrayC[-0.55065949, 6.03534661, 0.01111456]) 23 } 24 25 # functions 26 27 Run your program as often as you'd like, before submitting for grading. Below, type any needed












