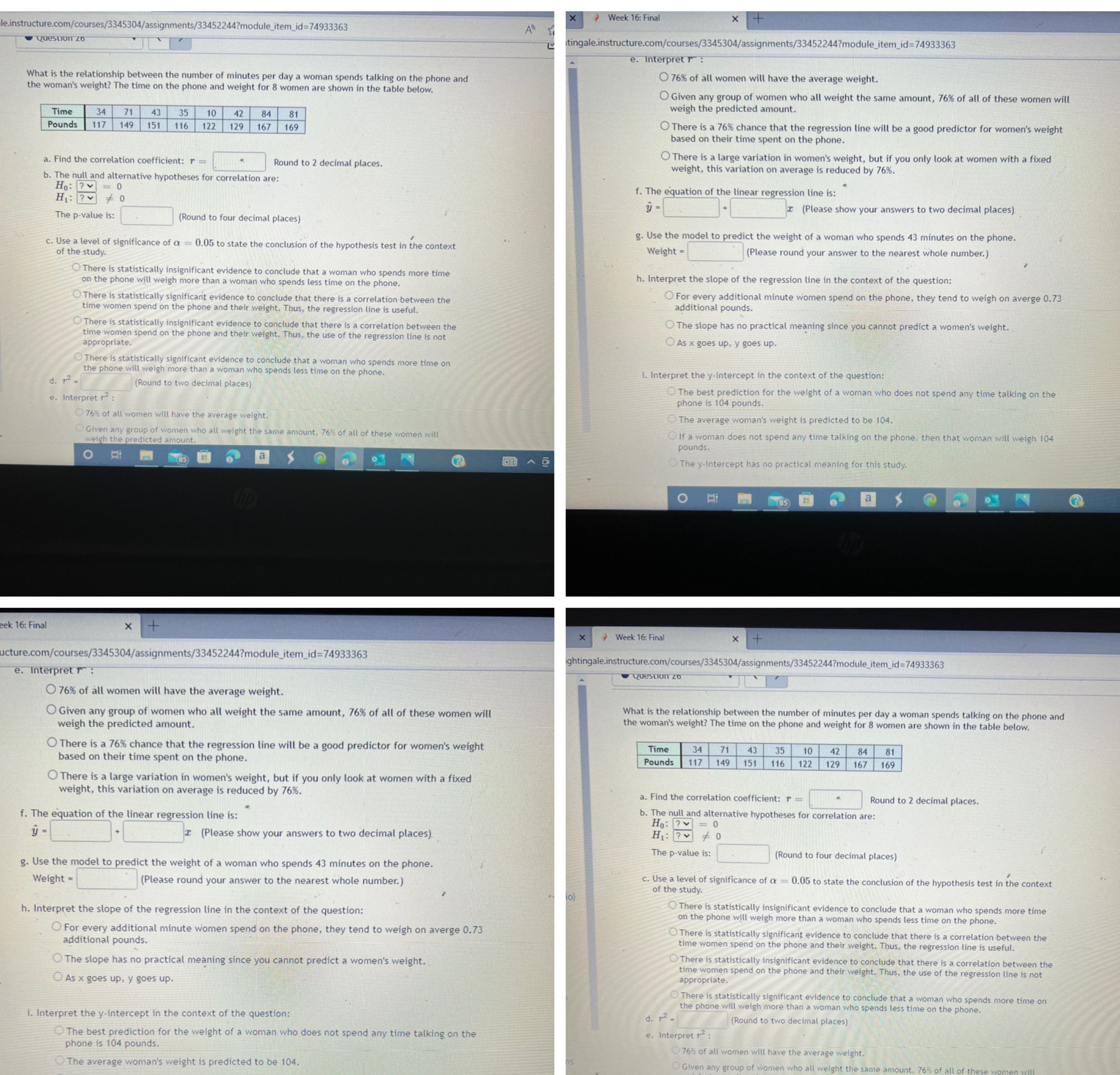
All the questions on this picture please answer all
* Week 16: Final e.instructure.com/courses/3345304/assignments/33452244?module_item_id=74933363 oz uonsand itingale.instructure.com/courses/3345304/assignments/33452244?module_item_id=74933363 e. Interpret T: What is the relationship between the number of minutes per day a woman spends talking on the phone and O 76% of all women will have the average weight. the woman's weight? The time on the phone and weight for 8 women are shown in the table below. Given any group of women who all weight the same amount, 76% of all of these women will weigh the predicted amount. Time 34 71 43 35 10 42 84 8 Pounds 117 149 151 116 122 129 167 169 There is a 76% chance that the regression line will be a good predictor for women's weight based on their time spent on the phone. There is a large variation in women's weight, but if you only look at women with a fixed a. Find the correlation coefficient: T - Round to 2 decimal places. weight, this variation on average is reduced by 76%. . The null and alternative hypotheses for correlation are: Ho: ?= f. The equation of the linear regression line is: H1: ? ~ #0 y = I (Please show your answers to two decimal places). The p-value is: (Round to four decimal places) g. Use the model to predict the weight of a woman who spends 43 minutes on the phone. c. Use a level of significance of a = 0.05 to state the conclusion of the hypothesis test in the context of the study. Weight = (Please round your answer to the nearest whole number.) There is statistically insignificant evidence to conclude that a woman who spends more time h. Interpret the slope of the regression line in the context of the question: on the phone will weigh more than a woman who spends less time on the phone. There is statistically significant evidence to conclude that there is a correlation between the O For every additional minute wo spend on the phone, they tend to weigh on averge 0.73 time women spend on the phone and their weight. Thus, the regression nation-be he regression line is useful. additional pounds. There is statistically insignificant evidence to conclude that there is a correlation between the The slope has no practical meaning since you cannot predict a women's weight. appropriate. time women spend on the phone and their weight. Thus, the use of the regression line is not O As x goes up, y goes up. There is statistically significant evidence to conclude that a woman who spends more time on the phone will weigh more than a woman who ends less time on the phone. . Interpret the y-intercept in the context of the question: d. r = (Round to two decimal places) The best prediction for the weight of a woman who does not spend any time talking on the e. Interpret 72 : phone is 104 pounds. 76% of all women will have the average weight. The average woman's weight is predicted to be 104. wiven any group of women who all weight the same amount, 76 of all of these women will he talking on the phone, then that woman will weigh 104 pounds . a N The y-intercept has no practical meaning for this study. eek 16: Final x x Week 16: Final x ucture.com/courses/3345304/assignments/33452244?module_item_id=74933363 ghtingale.instructure.com/courses/3345304/assignments/33452244?module_item_id=74933363 e. Interpret T : 76% of all women will have the average weight. Given any group of women who all weight the same amount, 76% of all of these women will What is the relationship between the number of minutes per day a woman spends talking on the phone and weigh the predicted amount. the woman's weight? The time on the phone and weight for 8 women are shown in the table below. There is a 76% chance that the regression line will be a good predictor for women's weight Time 71 43 35 10 42 84 81 based on their time spent on the phone. Pounds 117 149 151 116 122 129 167 169 There is a large variation in women's weight, but if you only look at women with a fixed weight, this variation on average is reduced by 76%. a. Find the correlation coefficient: 7 - Round to 2 decimal places. f. The equation of the linear regression line is: b. The null and alternative hypotheses for correlation are: Ho: ? = 0 y = T (Please show your answers to two decimal places). H1: ?v The p-value is: (Round to four decimal places) g. Use the model to predict the weight of a woman who spends 43 minutes on the phone. Weight = (Please round your answer to the nearest whole number.) . Use a level of significance of a = 0.05 to state the conclusion of the hypothesis test in the context of the study. There is statistically insignificant evidence to conclude that a woman who spends more time h. Interpret the slope of the regression line in the context of the question: on the phone will weigh more than a woman who spends less time on the phone. For every additional minute women spend on the phone, they tend to weigh on averge 0.73 There is statistically significant evidence to conclude that there is a correlation between the additional pounds. time women spend on the phone and their weight. Thus, the regression line is uses The slope has no practical meaning since you cannot predict a women's weight. There is statistically insignificant evidence to conclude that there is a correlation between the As x goes up, y goes up. appropriate. time women spend on the phone and their weight. Thus, the use of the regression line is not There is statistically significant evidence to conclude that a woman who spends more time on the phone will weigh more than a woman who spends less time on the phone. i. Interpret the y-intercept in the context of the question: d. 72 - (Round to two decimal places) The best prediction for the weight of a woman who does not spend any time talking on the e. Interpret r2 : phone is 104 pounds. 76% of all w he average weight. The average woman's weight is predicted to be 104