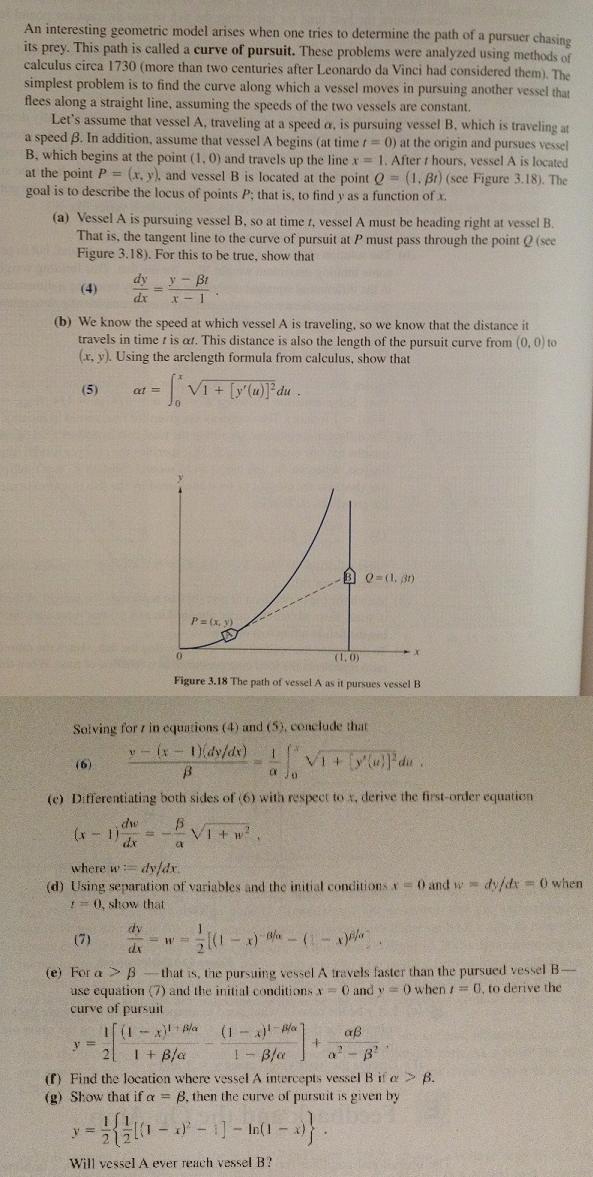
An interesting geometric model arises when one tries to determine the path of a pursuer chasine its prey. This path is called a curve of pursuit. These problems were analyzed using methods of calculus circa 1730 (more than two centuries after Leonardo da Vinci had considered them). The simplest problem is to find the curve along which a vessel moves in pursuing another vessel that flees along a straight line, assuming the speeds of the two vessels are constant. Let's assume that vessel A, traveling at a speed a, is pursuing vessel B. which is traveling at a speed B. In addition, assume that vessel A begins (at time t 0) at the origin and pursues vessel B, which begins at the point (1, 0) and travels up the line x= 1, After t hours, vessel A is located at the point P = (x, y), and vessel B is located at the point Q = (1. Br) (see Figure 3.18). The goal is to describe the locus of points P; that is, to find y as a function of x. (a) Vessel A is pursuing vessel B, so at time t, vessel A must be heading right at vessel B. That is, the tangent line to the curve of pursuit at P must pass through the point Q (see Figure 3.18). For this to be true, show that dy y - Bi (4) dx x-1 (b) We know the speed at which vessel A is traveling, so we know that the distance it travels in time t is at. This distance is also the length of the pursuit curve from (0, 0) to (r, y). Using the arclength formula from calculus, show that (5) Vi + [y(u)]*du at= P= (x, V) (1,0) Figure 3.18 The path of vessel A as it pursues vessel B Solving for i in equations (4) and (5), conclude that v- ( - 1)(dy/dx) VI+ y]'du. (6) (e) Differentiating both sides of (6) with respect to x, derive the first-order equation dw (x- 1 where w= dyfdr. (d) Using separation of variables and the initial conditions= 0 and w dy/dx = 0 when = 0, show that dv (7) - x) a - (1- W (e) For a > B use equation (7) and the initial conditions =0 and v = ) when = 0, to derive the curve of pursuit that is, the pursuing vessel A travels faster than the pursued vessel B- (1 - - Bla 1- B/a a 2 I + B/a a - B' (f) Find the location where vessel A intercepts vessel B if e >> B. (g) Show that if a = B. then the curve of pursuit is given by In(1 Will vessel A ever reach vessel B?