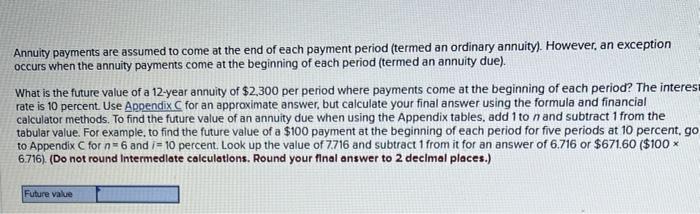
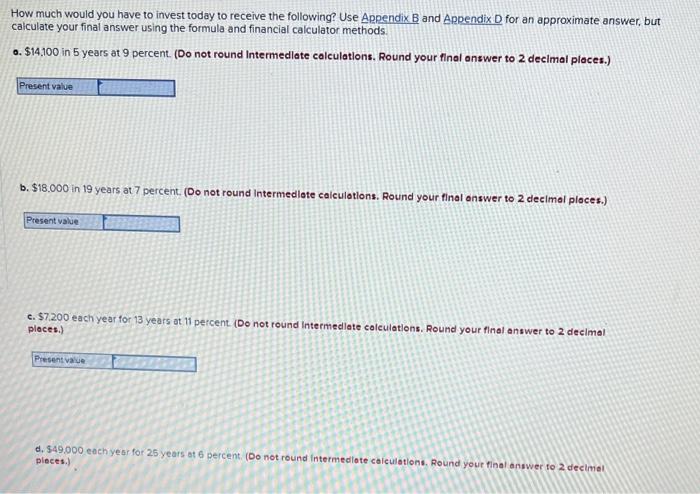
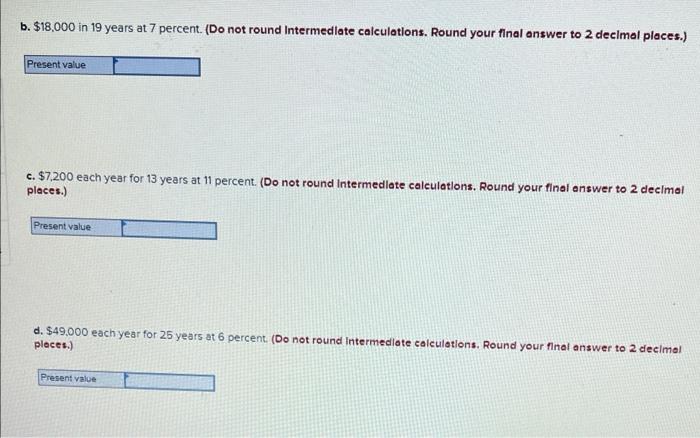
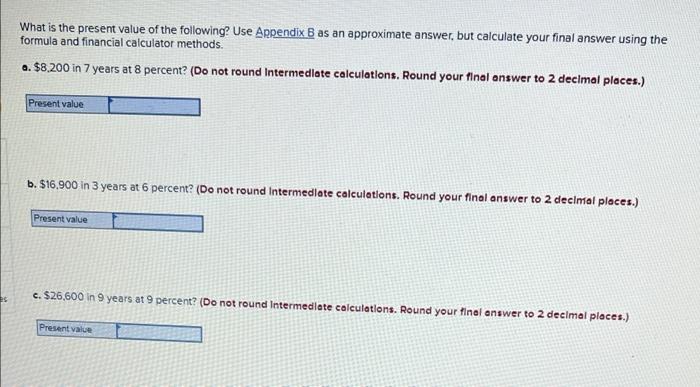
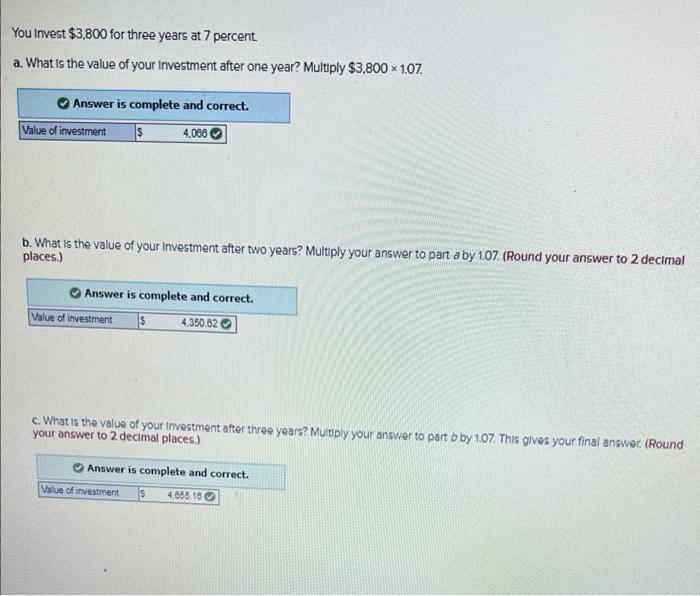
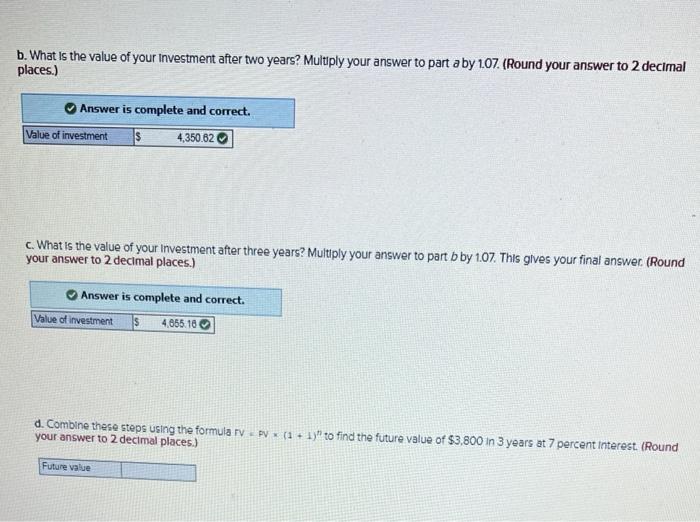
Annuity payments are assumed to come at the end of each payment period (termed an ordinary annuity). However, an exception occurs when the annuity payments come at the beginning of each period (termed an annuity due) What is the future value of a 12-year annuity of $2,300 per period where payments come at the beginning of each period? The interesa rate is 10 percent. Use Appendix for an approximate answer, but calculate your final answer using the formula and financial calculator methods. To find the future value of an annuity due when using the Appendix tables, add 1 to n and subtract 1 from the tabular value. For example, to find the future value of a $100 payment at the beginning of each period for five periods at 10 percent go to Appendix C for n=6 and = 10 percent. Look up the value of 7716 and subtract 1 from it for an answer of 6.716 or $671.60 ($100 * 6.716). (Do not round Intermediate calculations. Round your final answer to 2 decimal places.) Future value How much would you have to invest today to receive the following? Use Appendix B and Appendix D for an approximate answer, but calculate your final answer using the formula and financial calculator methods. 0. $14,100 in 5 years at 9 percent. (Do not round Intermediate calculations. Round your final answer to 2 decimal places.) Present value b. $18.000 in 19 years at 7 percent. (Do not round Intermediate calculations. Round your final answer to 2 decimal places.) Present value c. $7.200 each year for 13 years at 11 percent. (Do not round Intermediate calculations. Round your final answer to 2 decimal places.) Presenta d. 549.000 each year for 25 years 6 6 percent (Do not round Intermediate calculations, Round your final answer to 2 decimal places.) b. $18,000 in 19 years at 7 percent. (Do not round Intermediate calculations. Round your final answer to 2 decimal places.) Present value c. $7,200 each year for 13 years at 11 percent. (Do not round Intermediate calculations. Round your final answer to 2 decimal places.) Present value d. $49.000 each year for 25 years at 6 percent (Do not round Intermediate calculations. Round your final answer to 2 decimal ploces.) Present value What is the present value of the following? Use Appendix B as an approximate answer, but calculate your final answer using the formula and financial calculator methods. a. $8.200 in 7 years at 8 percent? (Do not round Intermediate calculations. Round your final answer to 2 decimal places.) Present value b. $16.900 in 3 years at 6 percent? (Do not round Intermediate calculations. Round your final answer to 2 decimal places.) Present value c. $26.600 in 9 years at 9 percent? (Do not round Intermediate calculations. Round your final answer to 2 decimal places.) Present value You Invest $3,800 for three years at 7 percent a. What is the value of your investment after one year? Multiply $3,800 * 1.07. Answer is complete and correct. Value of investment 15 4.066 b. What is the value of your investment after two years? Multiply your answer to part aby 1.07. (Round your answer to 2 decimal places.) Answer is complete and correct. Value of investment 15 4,350.62 c. What is the value of your investment after three years? Multiply your answer to part b by 1.07. This gives your final answer (Round your answer to 2 decimal places.) Answer is complete and correct. Value of investment 15 4535.16 b. What is the value of your investment after two years? Multiply your answer to part aby 1.07. (Round your answer to 2 decimal places.) Answer is complete and correct. Value of investment s 4,350.62 c. What is the value of your Investment after three years? Multiply your answer to part b by 1.07. This gives your final answer (Round your answer to 2 decimal places.) Answer is complete and correct. Value of investment 15 4,655.10 d. Combine these steps using the formula IV = PV = (1 + 1y" to find the future value of $3,800 in 3 years at 7 percent interest. (Round your answer to 2 decimal places.) Future value