Question
Answer all please. Sports Fashion produces four (4) types of protective jackets for sports enthusiasts: J1, J2, J3 and J4. Each J1 requires 4 minutes
Answer all please.
Sports Fashion produces four (4) types of protective jackets for sports enthusiasts: J1, J2, J3 and J4. Each J1 requires 4 minutes of machine time, 40 minutes of labour and 3 units of protective shell materials. Each J2 requires 6 minutes of machine time, 90 minutes of labour and 5 units of protective shell materials. J3 and J4 are their premium models which they purchase the semi-finished jackets from a contractor in Italy. J3 and J4 both require 8 minutes of machine time and 50 minutes of labour each. Each J3 and J4 only require 1 unit of protective shell materials to complete its production.
The unit cost (i.e., per jacket) for J1, J2, J3 and J4 are $10, $16, $24 and $30, respectively. The management has given the following guidance:
The markup percentages (markup percentage = (unit profit) (unit cost) 100%) for J1 and J2 are set at 20%, while those for J3 and J4 are set at 28%. Maximising profit is the main priority.
Based on the past sales data, combined demand for J3 and J4 is not more than 30% of the combined sales for J1 and J2. Thus, the production ratio for J3 and J4 should also be kept to not more than 30% of the combined production for J1 and J2.
J2 is a popular jacket and its production should be at least twice as many as J1.
There are 40 machining hours and 300 labour hours available per week.
There are 1,000 units of protective shell materials available per week.
The weekly production budget is set at $5,000.
(a) Apply and state the complete linear programming model for the production problem faced by Sports Fashion. State any two (2) assumptions relevant to the case.
(b) Solve the linear programming model in Question 1(a) using Microsoft Excel Solver and state the optimal solution. You are required to copy and paste the Answer Report and Sensitivity Report from your Solver results. (Hint: Select Simplex LP as your solving method in Solver).
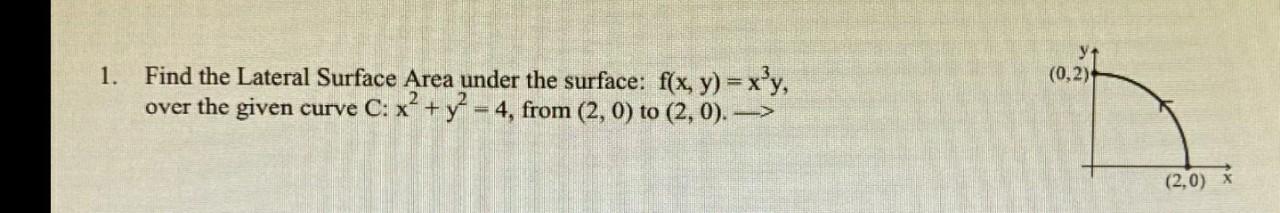


Step by Step Solution
There are 3 Steps involved in it
Step: 1

Get Instant Access to Expert-Tailored Solutions
See step-by-step solutions with expert insights and AI powered tools for academic success
Step: 2

Step: 3

Ace Your Homework with AI
Get the answers you need in no time with our AI-driven, step-by-step assistance
Get Started


