Answer in Java. Do Part 3, Part 4, and Part 5. I have included the code for Part 1 and Part 2 below the instructions, and I also included a picture of the "algorithm of infix to postfix translation which is introduced in the lecture" that is mentioned in the instructions for Part 3.

Code for Part 1 and Part 2:

"algorithm of infix to postfix translation which is introduced in the lecture"

Again, answer part 3, part 4, and part 5.

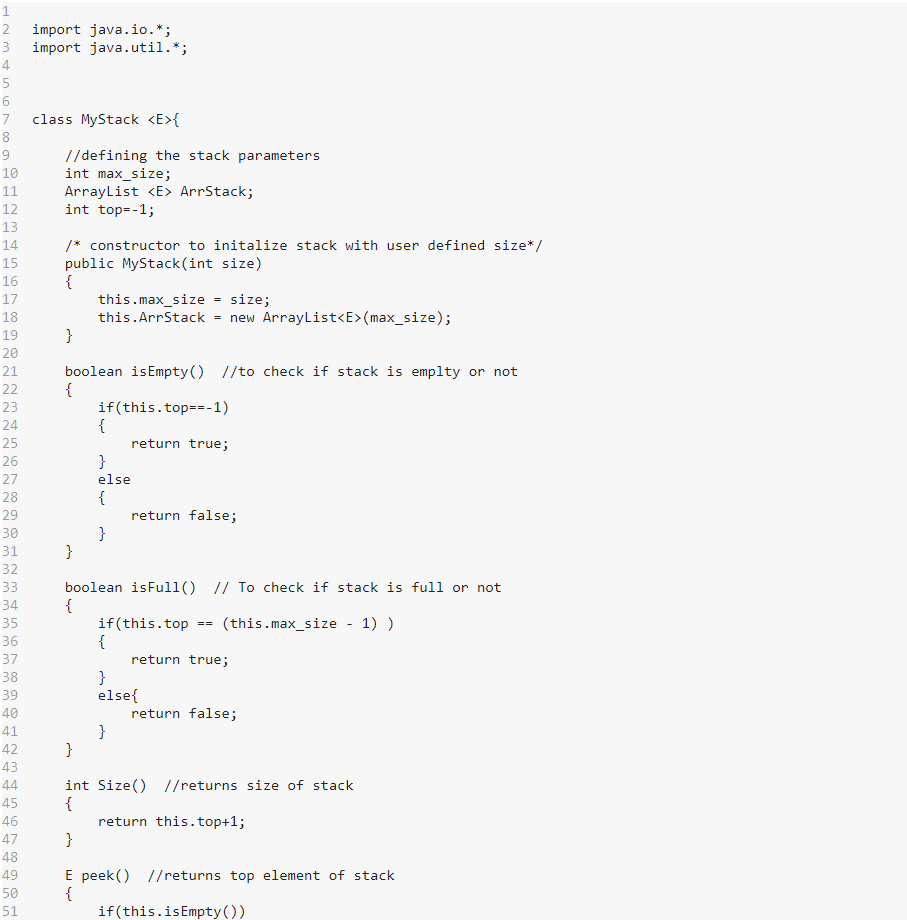
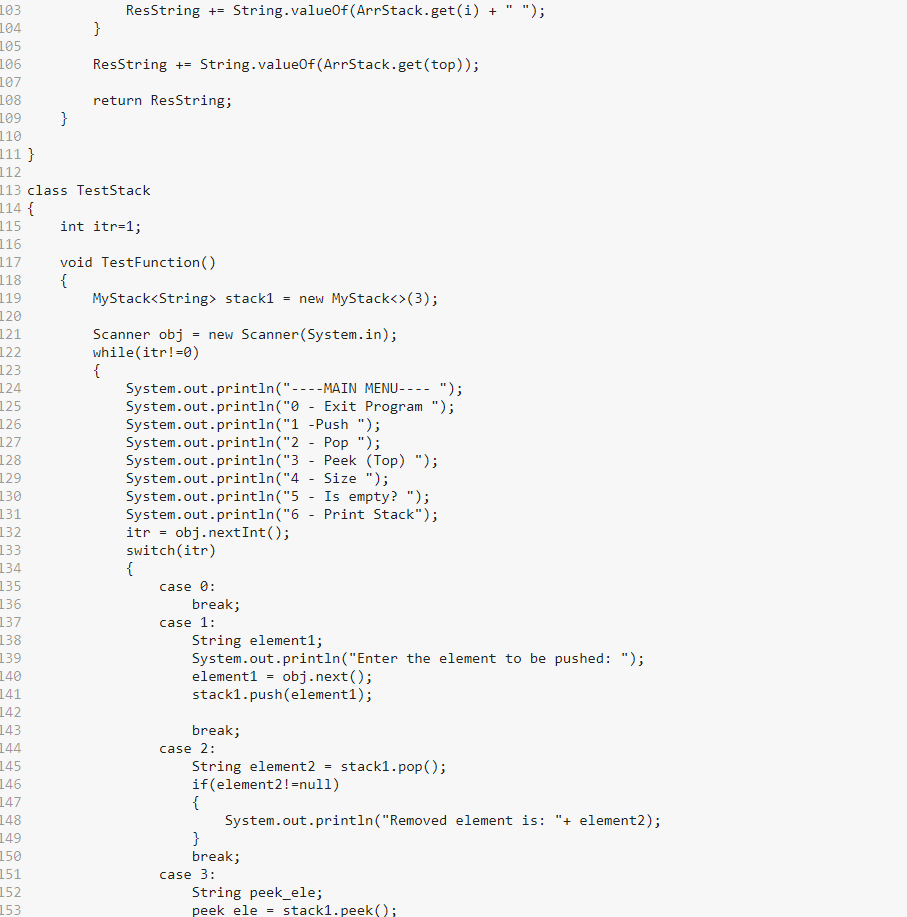
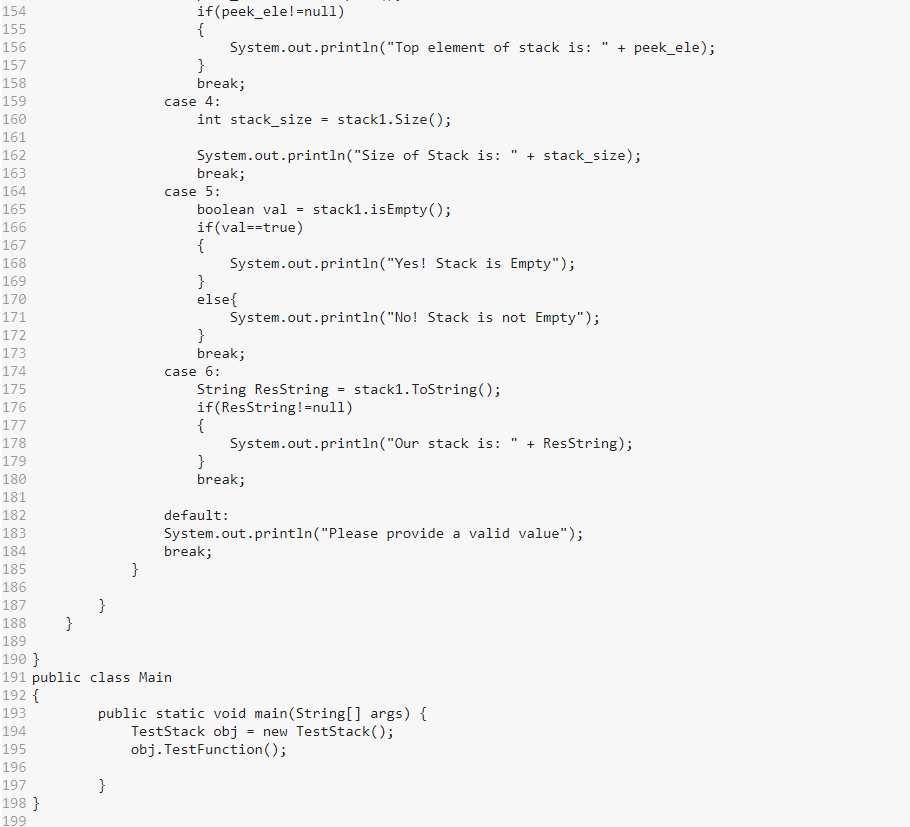
The goal for this assignment is to implement Stack ADT using ArrayList or LinkedList implementation. Then, write a program to use an object of the developed Stack class to solve simple and practical problems. Please name the programs as indicated and add proper program headers and output labels and comments. Part 1: (20 points) Develop a new class, called MyStackYourname, to implement, among others, key stack operations [push (e), pop (), peek (), size (), isEmpty(),tostring ()] we discussed in the class. Class Stack needs to be defined as generic stack with type so that we can create stack objects that can hold data of different types, such as integer stack, string stack, char stack, double stack, etc. MystackYourname Class must have these methods Please consider how to handle boundary conditions (stack empty, etc.) for these methods. You should write your own code to handle those boundary conditions instead of just letting the code throw a NullPointerException or ArrayIndexQutQfBoundsException Next, develop a simple test program called TestStackYourname to test each stack operation listed above and defined in your class MyStackYourname. Try String type stack for the test program. Use proper labels. Make sure to allow the user to enter the stack content using interactive menu (embedded inside the sentinel loop to allow re-run): ---MAIN MENU---- 0 - Exit Program 1 - Push 2 - Pop 3 - Peek (Top) 4 - Size 5 - Is Empty? 6 - Print stack Choose menu: Again, you cannot change method names, return type and parameter types. To evaluate your Class's methods, the instructor may use another Test Program and will use your methods. // We will use main method (check Part 5) for testing both Part 3 and 4 at once Use your MyStackYourname to write the procedure of transformation from infix to postfix. Use the algorithm of infix to postfix translation which is introduced in the lecture, translate infix expression to postfix expression. Assumption: Input infix string doesn't have whitespaces. All input number is one-digit number (positive digit 0 to 9 ) Input infix can include parenthesis Operator +/ can be used The output postfix string doesn't have whitespaces. Part 4: (10 points) In the ExprYourname class, implement another method, call it postfixEval. Using class MystackYourname, the postfixEval method should evaluate a postfix expression and return the correct calculated result. Write a method public static double postfixEval(String postfix) // Write appropriate codes here // Return calculated result value \} Assumption: Input postfix string doesn't have whitespaces. All input number is one-digit number (positive digit 0 to 9 ) Operator + can be used. Part 5: (10 points) In the Expryourname class, write a main method which tests above two methods (Part 3 and Part 4) Write a method public static void main(string[] arg) \{ // What is the process of main method. // - User will insert infix // - Invoke infixtoPostfix to transform it to postfix expression // - Invoke postfixEval to evaluate postfix expression // - Show the calculated result // Write appropriate codes here // Allow the user re-run the program 3 // Examples Enter an infix: (7+3)(31)/2 //Red characters are user input Postfix Expression: 73+312/ Result value: 10.0 Do you want to continue? (Y/N)Y Enter an infix: (56)/42(5+2) Postfix Expression: 564/252+ Result value: 7.5 Do you want to continue? (Y/N)Y Enter an infix: 3+2==(2+3) Postfix Expression: 3223++ Result value: 35.0 Do you want to continue? (Y/N) N ass Main dblic static void main(String[] args) \{ TestStack obj = new TestStack () ; obj. TestFunction (); Infix Transformation to Postfix Algorithm: 1. Create an empty stack and an empty output string 2. Scan infix input string from left to right 3. If the current input token is an operand, append it to the output string. 4. If the current input token is an operator, pop off all operators that have equal or higher and append them to the output string; then push the current operator onto the stack. - If stack has '(' on the top, stop popping 5. If the current input token is '(', push it onto the stack. 6. If the current input token is ')', pop off all operators and append them to the output string until a '(' is popped; discard the '(