Answer the following questions

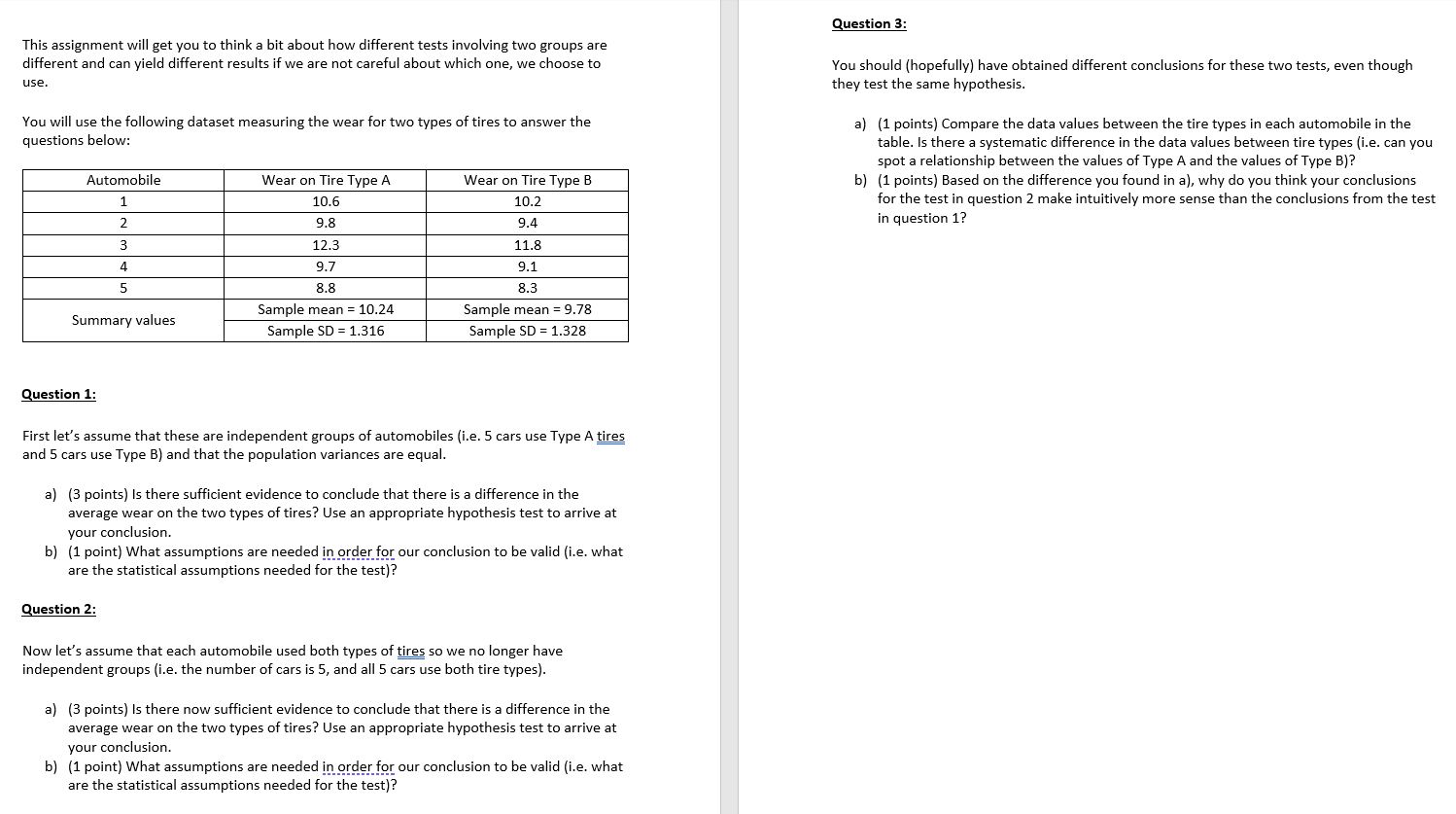
Question 3: This assignment will get you to think a bit about how different tests involving two groups are different and can yield different results if we are not careful about which one, we choose to You should (hopefully) have obtained different conclusions for these two tests, even though use. they test the same hypothesis. You will use the following dataset measuring the wear for two types of tires to answer the a) (1 points) Compare the data values between the tire types in each automobile in the questions below: table. Is there a systematic difference in the data values between tire types (i.e. can you spot a relationship between the values of Type A and the values of Type B)? Automobile Wear on Tire Type A Wear on Tire Type B b) (1 points) Based on the difference you found in a), why do you think your conclusions 10.6 10.2 for the test in question 2 make intuitively more sense than the conclusions from the test 2 9.8 9.4 in question 1? 3 12.3 11.8 4 9.7 9.1 5 8.8 8.3 Sample mean = 10.24 Sample mean = 9.78 Summary values Sample SD = 1.316 Sample SD = 1.328 Question 1: First let's assume that these are independent groups of automobiles (i.e. 5 cars use Type A tires and 5 cars use Type B) and that the population variances are equal. a) (3 points) Is there sufficient evidence to conclude that there is a difference in the average wear on the two types of tires? Use an appropriate hypothesis test to arrive at your conclusion. b) (1 point) What assumptions are needed in order for our conclusion to be valid (i.e. what are the statistical assumptions needed for the test)? Question 2: Now let's assume that each automobile used both types of tires so we no longer have independent groups (i.e. the number of cars is 5, and all 5 cars use both tire types). a) (3 points) Is there now sufficient evidence to conclude that there is a difference in the average wear on the two types of tires? Use an appropriate hypothesis test to arrive at your conclusion. b) (1 point) What assumptions are needed in order for our conclusion to be valid (i.e. what are the statistical assumptions needed for the test)