
Answer the questions below well
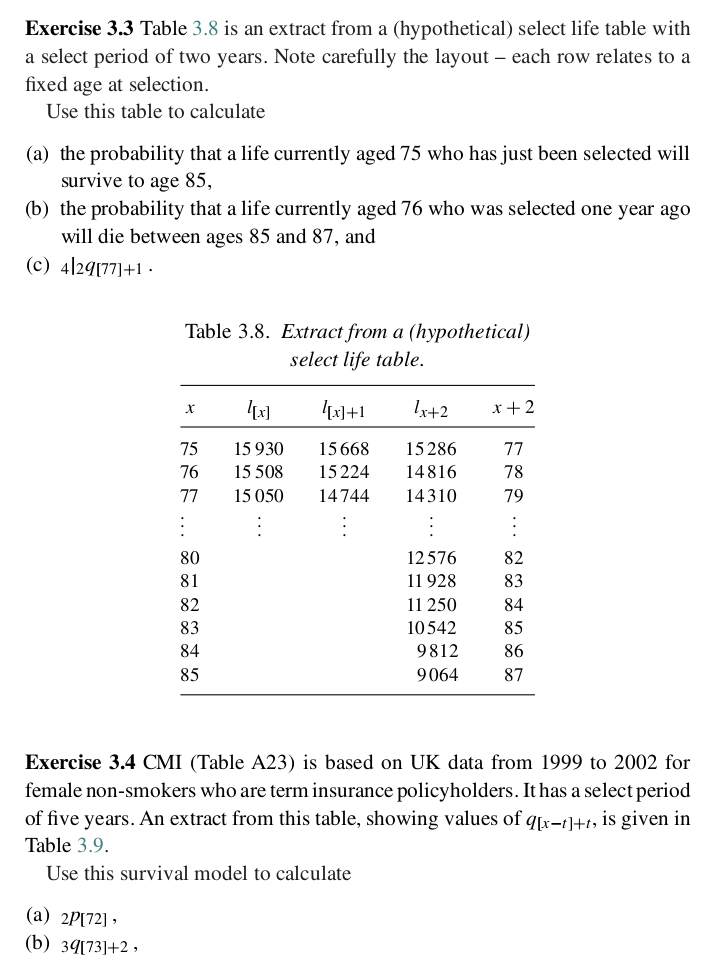
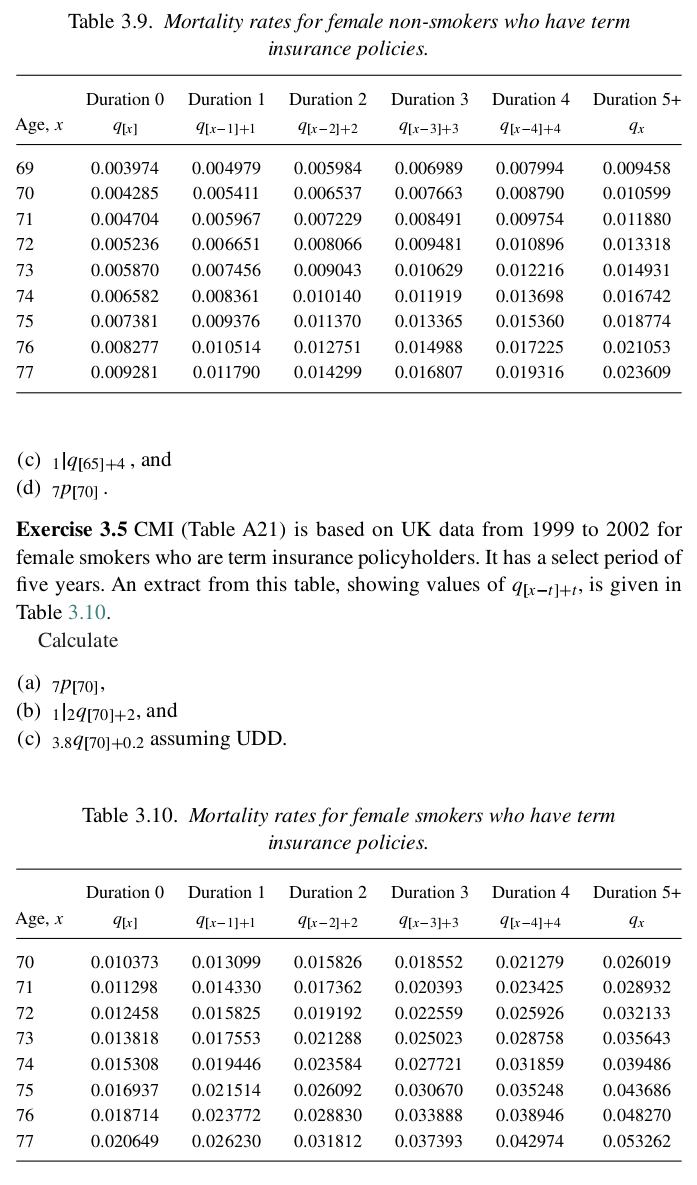
A company examining its employee retention rates considers the number of complete years a new employee works for a particular division before leaving. The results are shown in the table below: Division A 6 Division B 00 00 00 Division C 10 5 7 (i) Perform a one-way analysis of variance at the 5% level to compare the retention rates for the three divisions. [5] (ii) Present the data in a simple diagram and hence comment briefly on the validity of the assumptions required for the analysis of variance. [2] (iii) Concern is expressed over the variability of the results in Division B. It is thought that this might be significantly different from the assumed common underlying variance. (a) Write down an estimate for the underlying common variance for all three divisions. (b) Calculate an unbiased estimate for the variance in Division B based on the data for Division B only. (c) Test at the 5% level whether the variance in Division B is significantly different from your estimate in (iii)(a). [5] [Total 12]Exercise 3.3 Table 3.8 is an extract from a (hypothetical) select life table with a select period of two years. Note carefully the layout - each row relates to a fixed age at selection. Use this table to calculate (a) the probability that a life currently aged 75 who has just been selected will survive to age 85, (b) the probability that a life currently aged 76 who was selected one year ago will die between ages 85 and 87, and (c) 4 29[77]+1 . Table 3.8. Extract from a (hypothetical) select life table. X [[x] [x]+1 1x+ 2 x+2 75 15 930 15 668 15286 77 76 15 508 15 224 14816 78 77 15 050 14744 14310 79 . 80 12576 82 81 11 928 83 82 11 250 84 83 10542 85 84 9812 86 85 9064 87 Exercise 3.4 CMI (Table A23) is based on UK data from 1999 to 2002 for female non-smokers who are term insurance policyholders. It has a select period of five years. An extract from this table, showing values of qux-]+, is given in Table 3.9. Use this survival model to calculate (a) 2P[72] , (b) 39[73]+2 ,Table 3.9. Mortality rates forfomoio non-smokers who have term insurance policies. Duration 0 Duration 1 Duration 2 Duration 3 Duration 4 Duration 5+ A36. I on] tip: 11+1 fin2H2 fin3H3 4' [x4]+4 9'1 69 0.003914 0.004919 0.005934 0.006939 0.001994 0.{319453 10 0.004235 0.005411 0.006531 0.1111663 0.003190 0.010599 11 0.004104 0.005961 0.001229 0.003491 0.009154 0.011330 12 0.005236 0.006651 0.003066 0.009431 0.010396 0.013313 13 0.005310 0.001456 0.009043 0.010629 0.012216 0.014931 14 0.006532 0.110336] 0.010140 0.011919 0.013693 0.016142 15 0.001331 0.009316 0.011310 0.013365 0.015360 0.013114 16 0.003211 0.010514 0.012151 0.014933 0.011225 0.021053 11 0.009231 0.011190 0.014299 0.016301 0.019316 0.023609 (6) 1|4[65]+4. and ((1) 7pm] - Exercise 3.5 CMI (Table A21) is based on UK data from 1999 to 2002 for female smokers who are term insurance policyholders. It has a select period of ve years. An extract from this table, showing values of q[x_;]+t, is given in Table 3 .10. Calculate (a) apno]. (b) 1|2i[10]+2. and (C) 3_3q[7]+_2 assuming UDD. Table 3.10- Mortality rates forfomoio smokers who have term insurance policies. Duration 0 Duration 1 Duration 2 Duration 3 Duration 4 Duration 5+ 436:1 41x] 9LT 11+1 tin21+: tax3H3 4a41+4 4x 10 0.010313 0.013099 0.015326 0.013552 0.021219 0.026019 11 0.011293 0.014330 0.011362 0.020393 0.023425 0.023932 12 0.012453 0.015325 0.019192 0.022559 0.025926 0.032133 13 0.013313 0.011553 0.021233 0.025023 0.023153 0.035643 14 0.015303 0.019446 0.023534 0.021121 0.031359 0.039436 15 0.016931 0.021514 0.026092 0.030610 0.035243 0.043636 16 0.013114 0.023112 0.023330 0.033333 0.033946 0.043 210 11 0.020649 0.026230 0.031312 0.031393 0.042914 0.053262












