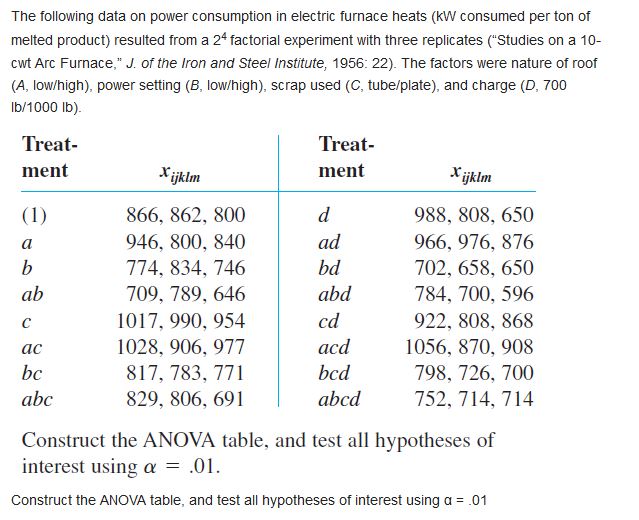
Answer these questions:

\fIdentify the statistical population, sample, and variable of interest in each of the following situations: (a) To learn about starting salaries for engineers graduating from a Midwestern university, twenty graduating seniors are asked to report their starting salary. (b) Fifty computer memory chips were selected from the thousand manufactured that day. The computer memory chips were tested, and 5 were found to be defective. (c) Tensile strength was measured on 20 specimens made of a new plastic material. The intent is to learn about the tensile strengths for all specimens that could conceivably be manufactured with the new plastic material.The article "The Foreman's View of Quality Control" (Quality Engr., 1990: 257-280) described an investigation into the coating weights for large pipes resulting from a galvanized coating process. Production standards call for a true average weight of 200 lb per pipe. The accompanying descriptive summary and boxplot are from Minitab Variable N Mean Median TrMean StDev SEMean ctg wt 30 206.73 206.00 206.81 6.35 1 . 16 Variable Min Max 03 ctg wt 193 . 00 218.00 202.75 212. 00 Coating weight 190 200 210 220 a. What does the boxplot suggest about the status of the specification for true average coating weight? b. A normal probability plot of the data was quite straight. Use the descriptive output to test the appropriate hypotheses.Consider the largesample level .01 test in Section 8.3 for testing Hp : p = .2 against Ha : p > .2. a. For the arternathre value , compute M21) for sample sizes n = 100, 2500, 10,000, 40,000, and 90,000. b. For H0: P = :2 against H33)\" 3: _2_ , compute the Pvalue when n = 100, 2500, 10,000, and 40,000. c. In most situations, would it be reasonable to use a level .01 test in conjunction with a sample size of 40,000? Why or why not? An article in the Nov. 11, 2005, issue of the San Luis Obispo Tribune reported that researchers making random purchases at California Wal-Mart stores found scanners coming up with the wrong price 8.3% of the time. Suppose this was based on 200 purchases. The National Institute for Standards and Technology says that in the long run at most two out of every 100 items should have incorrectly scanned prices. a. Develop a test procedure with a significance level of (approximately) .05, and then carry out the test to decide whether the NIST benchmark is not satisfied. b. For the test procedure you employed in (a), what is the probability of deciding that the NIST benchmark has been satisfied when in fact the mistake rate is 5%