answer this question as soon as possible.

the worksheet 8 is given below

all the last three files are given below.

the first file is 1000 prime text it contain text 1 from 7919 numbers.

second file is cs2004.java

third file is scale solution.java

Solve this by using eclipse. answer as soon as possible.

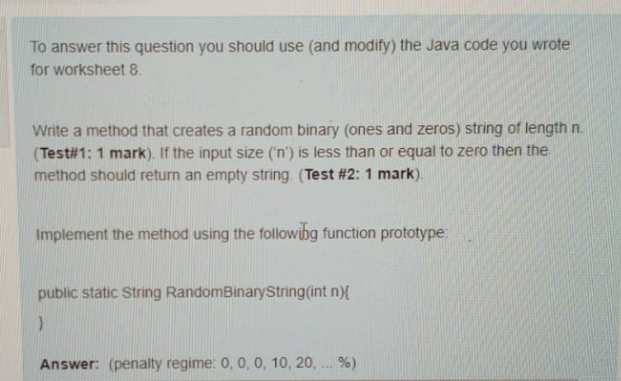
To answer this question you should use (and modify) the Java code you wrote for worksheet 8 Write a method that creates a random binary ones and zeros) string of length n. (Test#1: 1 mark). If the input size ('n') is less than or equal to zero then the method should return an empty string (Test #2: 1 mark). Implement the method using the followibg function prototype public static String RandomBinaryString(int n){ ) Answer: (penalty regime: 0, 0, 0, 10, 20, ... %) 1 and 1 inclusive. Run each test several times to verify that the list of numbers produced is different each time. 8.3 Exercise 2: The CS2004 Class Laboratory 8 Week 10 Fitness Functions the Scales Problem - 8.4 Exercise 3: The Scales Solution Class The CS2004 class contains some useful code for this laboratory and other laboratories. We will also be adding to and expanding on this class in later worksheets. Currently this class contains three static methods detailed as follows: 8.1 Introduction The ScalesSolution class contains a framework for implementing the fitness function and representation for the Scales problem. The class contains a String that holds the binary representation for a potential solution to a Scales problem. The fitness function applies the solution allocation represented by the string to set of weights passed as a parameter. static public int UI (int aa, int bb) Returns a uniformly distributed random integer between aa and bb inclusive. Firstly, the content of this worksheet is (may be) part of the Task #1 and Task #2 assessments. The attributes (data fields) and methods are as follows: static public double UR (double a, double b) Returns a uniformly distributed random double between a and b inclusive. This laboratory involves developing the fitness function for the Scales problem as discussed in the lecture. We are going to write a class that will generate a random solution and evaluate the fitness. This laboratory is VERY important since we will be using the code that we write in a number of subsequent laboratories and worksheets. private String scasol; This data field stores the representation solution for the Scales problem in question. 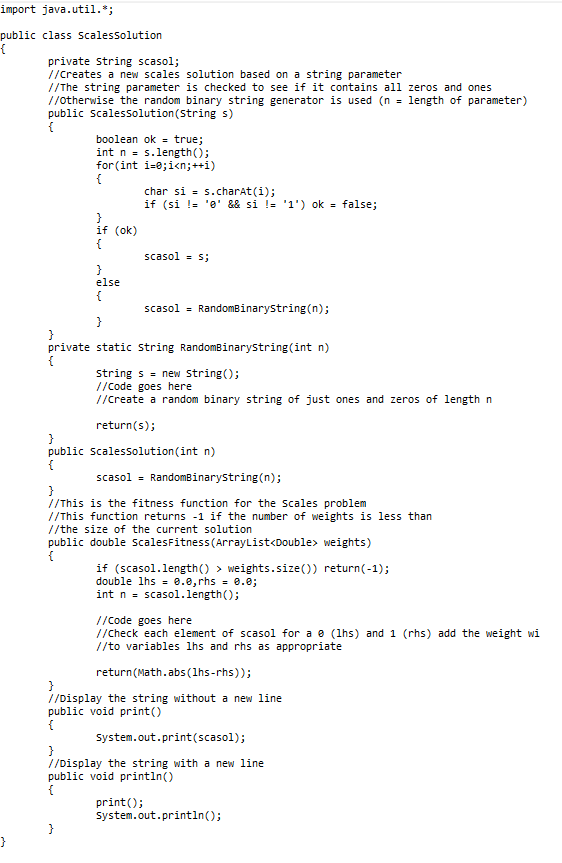static public ArrayList ReadNumberFile (String filename) Reads in a text file and parses all of the numbers in it, and returns an ArrayList of Double. We will use this method in exercise 8.5. 8.2 Exercise 1: Preliminaries public Scales Solution (String s) This constructor creates a solution from a specified String. If any character in the string is not a 'O' or 'l' then RandomBinaryString method is called with the size parameter set equal to the size of the parameter string that was passed. Add the following main method to the Lab8 class. Familiarise yourself with the lecture entitled 9.1 Search Algorithms, Representation, Fitness and Fitness Landscapes. Pay particular attention to the section on solving the Scales problem. public static void main(String args[]) { for (int i=0;i weights) This evaluates the fitness for the specified solution. An array of weights is passed as parameter. The function should return the Scales fitness function evaluated on the solution or -1 if there are fewer weights than the size of the solution. Note: this method is not complete and needs writing. You will need to complete both the RandomBinaryString and the Scales Fitness methods. The fitness function can be completed using the Pseudo-Code from the lecture. The RandomBinaryString method can be completed as follows: Generate a number (at least 100 each) of random Scales solutions for the first 10, 100, 250, 500 and 1000 primes numbers and evaluate (and average) their fitness. Is generating random solutions a good way of solving the Scales problem? What sizes could it work for? For each possible place in the string (n of them) you generate CS2004.UI (0,1). This will randomly generate a zero or one. If you get a zero add the character 'O' to the end of the string, otherwise add a 'l'. You will need to use a For loop. 8.6 Appendix A public void print() This displays the solution being represented with no new line. The following classes and text files contains the code and data you will need for this exercise sheet. public void println() This displays the solution being represented with a new line. Create an ArrayList containing the value 1, 2, 3, 4 and 10 as in the examples in the lecture. Test the fitness function on these examples (the ones from the lecture). Generate a number of random solutions and evaluate the fitness function on them, verify the accuracy manually. CS2004.java Implement the following code: Scales Solution s = new ScalesSolution ("10101"); s.println(); ScalesSolution.java 8.5 Exercise 4: Reading in Data 1000 Primes.txt This will create a new solution to the Scales problem of 5 weights called x with the odd weights on the right hand side of the scales and the even weights on the left hand side. End of document I What do you get if you run the following lines of code? The text file "1000 Primes.txt" contains (surprise, surprise) a list of the first 1000 prime numbers (http://mathworld.wolfram.com/PrimeNumber.html, http://oeis.org/A000040). We will be using these as the weights. The method ReadNumberFile within the class CS2004 can be used to read this file (and others in a similar format) into an ArrayList of Double. Read in the file and verify that this has been done correctly. s = new Scales Solution ("10101x"); s.println(); You will get nothing since the RandomBinaryString method has not been completed! When it is working, it should create a random binary string (a solution) of length six (given that the string passed as a parameter is not valid, i.e. not all 'O's or 'l's). For a small number of weights (say, less than ten) generate a number of random solutions to the Scales problems using the prime numbers (for example if you are solving it for 8 weights then the first 8 weights will be used by the fitness function) and verify the results manually. 1000Primes.txt - Notepad - File Edit Format View Help 7549 7559 7561 7573 7577 7583 7589 7591 7603 7607 7621 7639 7643 7649 7669 7673 7681 7687 7691 7699 7703 7717 7723 7727 7741 7753 7757 7759 7789 7793 7817 7823 7829 7841 7853 7867 7872 7877 7879 7883 7901 7987 7919 Ln 1, Col1 100% Windows (CRLF) Type here to search OBI A# C la UTF-8 09:27 PM 31/01/2021 import java.util.*; import java.io.*; == 1/Some useful code that we will probably reuse in later laboratories... public class CS2004 { //Shared random object static private Random rand; 1/Create a uniformly distributed random integer between aa and bb inclusive static public int UI (int aa, int bb) { int a = Math.min(aa, bb); int b = Math.max(aa, bb); if (rand null) { rand = new Random(); rand.setSeed (System.nanoTime()); } int d = b - a + 1; int x = rand.nextInt(d) + a; return(x); } 1/Create a uniformly distributed random double between a and b inclusive static public double UR(double a, double b) { if (rand == null) { rand = new Random(); rand.setSeed (System.nanoTime(); } return((b-a)*rand.nextDouble()+a); } //This method reads in a text file and parses all of the numbers in it //This code is not very good and can be improved! //But it should work!!! //It takes in as input a string filename and returns an array list of Doubles static public ArrayList ReadNumberFile(String filename) { ArrayList res = new ArrayList(); Reader r; try == { r = new BufferedReader(new FileReader(filename)); StreamTokenizer stok = new StreamTokenizer(r); stok.parseNumbers(); stok.nextToken(); while (stok.ttype != StreamTokenizer. TT_EOF) { if (stok.ttype StreamTokenizer. TT_NUMBER) { res.add(stok.nval); } stok.nextToken(); } } catch(Exception E) { System.out.println("+++ReadFile: "+E.getMessage()); } return(res); } } import java.util."; public class ScalesSolution { private String scasol; //creates a new scales solution based on a string parameter //The string parameter is checked to see if it contains all zeros and ones //otherwise the random binary string generator is used (n = length of parameter) public ScalesSolution(Strings) { boolean ok = true; int n = s.length(); for(int i=0;i weights) { if (scasol.length() > weights.size()) return(-1); double lhs = 0.0,rhs - 0.2; int n = scasol.length(); //Code goes here //Check each element of scasol for a m (1hs) and 1 (rhs) add the weight wi //to variables lhs and rhs as appropriate return(Math.abs(lhs-rhs)); } 1/Display the string without a new line public void print { System.out.print(scasol); } 1/Display the string with a new line public void println() { print(); System.out.println(); } } To answer this question you should use (and modify) the Java code you wrote for worksheet 8 Write a method that creates a random binary ones and zeros) string of length n. (Test#1: 1 mark). If the input size ('n') is less than or equal to zero then the method should return an empty string (Test #2: 1 mark). Implement the method using the followibg function prototype public static String RandomBinaryString(int n){ ) Answer: (penalty regime: 0, 0, 0, 10, 20, ... %) 1 and 1 inclusive. Run each test several times to verify that the list of numbers produced is different each time. 8.3 Exercise 2: The CS2004 Class Laboratory 8 Week 10 Fitness Functions the Scales Problem - 8.4 Exercise 3: The Scales Solution Class The CS2004 class contains some useful code for this laboratory and other laboratories. We will also be adding to and expanding on this class in later worksheets. Currently this class contains three static methods detailed as follows: 8.1 Introduction The ScalesSolution class contains a framework for implementing the fitness function and representation for the Scales problem. The class contains a String that holds the binary representation for a potential solution to a Scales problem. The fitness function applies the solution allocation represented by the string to set of weights passed as a parameter. static public int UI (int aa, int bb) Returns a uniformly distributed random integer between aa and bb inclusive. Firstly, the content of this worksheet is (may be) part of the Task #1 and Task #2 assessments. The attributes (data fields) and methods are as follows: static public double UR (double a, double b) Returns a uniformly distributed random double between a and b inclusive. This laboratory involves developing the fitness function for the Scales problem as discussed in the lecture. We are going to write a class that will generate a random solution and evaluate the fitness. This laboratory is VERY important since we will be using the code that we write in a number of subsequent laboratories and worksheets. private String scasol; This data field stores the representation solution for the Scales problem in question. static public ArrayList ReadNumberFile (String filename) Reads in a text file and parses all of the numbers in it, and returns an ArrayList of Double. We will use this method in exercise 8.5. 8.2 Exercise 1: Preliminaries public Scales Solution (String s) This constructor creates a solution from a specified String. If any character in the string is not a 'O' or 'l' then RandomBinaryString method is called with the size parameter set equal to the size of the parameter string that was passed. Add the following main method to the Lab8 class. Familiarise yourself with the lecture entitled 9.1 Search Algorithms, Representation, Fitness and Fitness Landscapes. Pay particular attention to the section on solving the Scales problem. public static void main(String args[]) { for (int i=0;i weights) This evaluates the fitness for the specified solution. An array of weights is passed as parameter. The function should return the Scales fitness function evaluated on the solution or -1 if there are fewer weights than the size of the solution. Note: this method is not complete and needs writing. You will need to complete both the RandomBinaryString and the Scales Fitness methods. The fitness function can be completed using the Pseudo-Code from the lecture. The RandomBinaryString method can be completed as follows: Generate a number (at least 100 each) of random Scales solutions for the first 10, 100, 250, 500 and 1000 primes numbers and evaluate (and average) their fitness. Is generating random solutions a good way of solving the Scales problem? What sizes could it work for? For each possible place in the string (n of them) you generate CS2004.UI (0,1). This will randomly generate a zero or one. If you get a zero add the character 'O' to the end of the string, otherwise add a 'l'. You will need to use a For loop. 8.6 Appendix A public void print() This displays the solution being represented with no new line. The following classes and text files contains the code and data you will need for this exercise sheet. public void println() This displays the solution being represented with a new line. Create an ArrayList containing the value 1, 2, 3, 4 and 10 as in the examples in the lecture. Test the fitness function on these examples (the ones from the lecture). Generate a number of random solutions and evaluate the fitness function on them, verify the accuracy manually. CS2004.java Implement the following code: Scales Solution s = new ScalesSolution ("10101"); s.println(); ScalesSolution.java 8.5 Exercise 4: Reading in Data 1000 Primes.txt This will create a new solution to the Scales problem of 5 weights called x with the odd weights on the right hand side of the scales and the even weights on the left hand side. End of document I What do you get if you run the following lines of code? The text file "1000 Primes.txt" contains (surprise, surprise) a list of the first 1000 prime numbers (http://mathworld.wolfram.com/PrimeNumber.html, http://oeis.org/A000040). We will be using these as the weights. The method ReadNumberFile within the class CS2004 can be used to read this file (and others in a similar format) into an ArrayList of Double. Read in the file and verify that this has been done correctly. s = new Scales Solution ("10101x"); s.println(); You will get nothing since the RandomBinaryString method has not been completed! When it is working, it should create a random binary string (a solution) of length six (given that the string passed as a parameter is not valid, i.e. not all 'O's or 'l's). For a small number of weights (say, less than ten) generate a number of random solutions to the Scales problems using the prime numbers (for example if you are solving it for 8 weights then the first 8 weights will be used by the fitness function) and verify the results manually. 1000Primes.txt - Notepad - File Edit Format View Help 7549 7559 7561 7573 7577 7583 7589 7591 7603 7607 7621 7639 7643 7649 7669 7673 7681 7687 7691 7699 7703 7717 7723 7727 7741 7753 7757 7759 7789 7793 7817 7823 7829 7841 7853 7867 7872 7877 7879 7883 7901 7987 7919 Ln 1, Col1 100% Windows (CRLF) Type here to search OBI A# C la UTF-8 09:27 PM 31/01/2021 import java.util.*; import java.io.*; == 1/Some useful code that we will probably reuse in later laboratories... public class CS2004 { //Shared random object static private Random rand; 1/Create a uniformly distributed random integer between aa and bb inclusive static public int UI (int aa, int bb) { int a = Math.min(aa, bb); int b = Math.max(aa, bb); if (rand null) { rand = new Random(); rand.setSeed (System.nanoTime()); } int d = b - a + 1; int x = rand.nextInt(d) + a; return(x); } 1/Create a uniformly distributed random double between a and b inclusive static public double UR(double a, double b) { if (rand == null) { rand = new Random(); rand.setSeed (System.nanoTime(); } return((b-a)*rand.nextDouble()+a); } //This method reads in a text file and parses all of the numbers in it //This code is not very good and can be improved! //But it should work!!! //It takes in as input a string filename and returns an array list of Doubles static public ArrayList ReadNumberFile(String filename) { ArrayList res = new ArrayList(); Reader r; try == { r = new BufferedReader(new FileReader(filename)); StreamTokenizer stok = new StreamTokenizer(r); stok.parseNumbers(); stok.nextToken(); while (stok.ttype != StreamTokenizer. TT_EOF) { if (stok.ttype StreamTokenizer. TT_NUMBER) { res.add(stok.nval); } stok.nextToken(); } } catch(Exception E) { System.out.println("+++ReadFile: "+E.getMessage()); } return(res); } } import java.util."; public class ScalesSolution { private String scasol; //creates a new scales solution based on a string parameter //The string parameter is checked to see if it contains all zeros and ones //otherwise the random binary string generator is used (n = length of parameter) public ScalesSolution(Strings) { boolean ok = true; int n = s.length(); for(int i=0;i weights) { if (scasol.length() > weights.size()) return(-1); double lhs = 0.0,rhs - 0.2; int n = scasol.length(); //Code goes here //Check each element of scasol for a m (1hs) and 1 (rhs) add the weight wi //to variables lhs and rhs as appropriate return(Math.abs(lhs-rhs)); } 1/Display the string without a new line public void print { System.out.print(scasol); } 1/Display the string with a new line public void println() { print(); System.out.println(); } }<><>