answer this question:

///////////////////////////////////////////////////////////

here are the ppt slides for your references:

:

a): ppt13 in LN03

:

b): ppt17 , LN03

:

c): eq 4.7

:

d): ppt20

:

e): page 30

:

f) page31-32

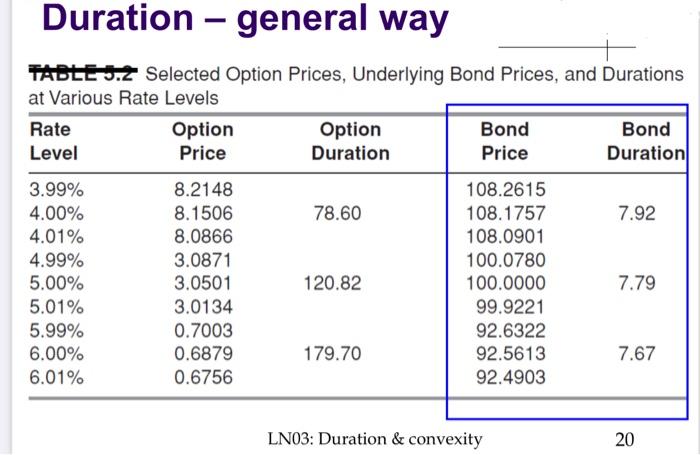
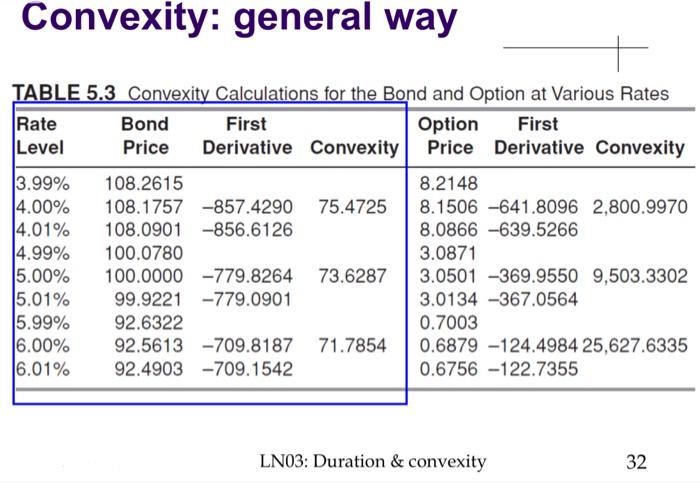
Calculate the requested measures in parts (a) through (f) for bonds A (assume that each bond pays interest semiannually): Bond A Coupon 8% Yield to maturity 8% Maturity (years) 2 Par $100.00 Price $100.00 (a) The dollar value of a basis point (ppt #13, LN03) (b) Macaulay duration (using the bond-rate function in compact form -- on ppt #17, LN03). (c) Modified duration (using the relation between modified duration and Macaulay duration, Eq. 4.7 on ppt #15, LN03). (d) The approximate duration by changing yields by +/-10 basis points (using the approximation method on ppt #20, LN03.) Compare your answers with Q3c. (e) Convexity measure (using the last equation - compact form - on ppt #30, LN03). (1) The approximate convexity measure by changing yields by +/-10 basis points (using the approximation method on ppt #31-32, LN3). Compare your answers with Q3e. - DV01 dollar value of 1 bp If yield changes by 1 basis point, how much the price changes in dollar value? 1 . DV01 = 10,000 Ay E.g.: if yield increases by 1 bp from 9% to 9.01%, the bond price drops from $100 to $99.96, DV01 = 0.04 E.g.: if yield increases by 50 bps from 9% to 9.5%, the price of this bond drops from $100 to $98.05 DV01 = Linearly related to the slope of the price-yield curve/positive related to price volatility/ sensitivity LN03: Duration & convexity 13 Duration: compact form 1+ y/ (1+y/2) y)(1+y/2) +! T D Mac 27 P 12 kl. 10-22h)-(00- 10 For 223)+(1005=12 5 1 1 T D Mod - 27 (1+y/2)27 y)(1+y/2)2T+ E.g.: a 5-year zero coupon bond selling to yield 9% c = 0,P = 100/(1.045)10 = 64.39,y=0.09,2T = 10 = = D Mac E.g.: a 5-year 9% bond selling to yield 9% C = 9,P =100, y=0.09,2T = 10 = D Mac LN03: Duration & convexity 17 1 21 t 100 D Mac +T 2T P. y Macaulay duration D Mac A simple transformation of Modified Duration DMac = (1+y/2)D Mod (4.7) DMac 2 D Mod c/2 *2 (1+y/2) (1+y/2) 100 (1+y/2) (1 + y/2) +Tx (4.5) Macaulay duration is a weighted average of terms, and the weight is percentage of discounted cash flows occurring at that term c/2 27 2T kx /) X LN03: Duration & convexity 15 Duration - general way TABLE 3.2 Selected Option Prices, Underlying Bond Prices, and Durations at Various Rate Levels Rate Option Option Bond Bond Level Price Duration Price Duration 3.99% 8.2148 108.2615 4.00% 8.1506 78.60 108.1757 7.92 4.01% 8.0866 108.0901 4.99% 3.0871 100.0780 5.00% 3.0501 120.82 100.0000 7.79 5.01% 3.0134 99.9221 5.99% 0.7003 92.6322 6.00% 0.6879 179.70 92.5613 7.67 6.01% 0.6756 92.4903 LN03: Duration & convexity 20 Convexity in compact form Convexity increases with the square of maturity Refer to #17, compact form of first derivative dP 1 T 1- + dy (1y/)?" y)(1+y/2)2T+1 dP 2c 1 2c T T(T +.5) 1 + 100- dy? (1+y/2)2T) y2 (1+y/2)2T+1 y)(1+y/2)2T+2 12c 1 2c T Convexity = T(T +.5) + 100 (1+y/2) y? (1+y/2)2+1 y)(1+y/2)2T+2 Tel.+2)+(1005)+ ( Guy2y) 42**( 1,3 1+ LN03: Duration & convexity 30 Approximate convexity day d dx dy dx d:x2 y' f"|y=5% Convexity yield price fly=5.00% Duration 4.99% Pt 4.995% fly=y' p+-po -1bp po-P -1bp 5% p+-p- -2bp PO 512 fr -1bp f" PO PO 5.005% 5.01% P C p+ - po po-p- -1bp -1bp -1bp * po II p+ + P--2p0 (Ay)2 * po Po LN03: Duration & convexity 31 Convexity: general way TABLE 5.3 Convexity Calculations for the Bond and Option at Various Rates Rate Bond First Option First Level Price Derivative Convexity Price Derivative Convexity 13.99% 108.2615 8.2148 14.00% 108.1757 -857.4290 75.4725 8.1506 -641.8096 2,800.9970 4.01% 108.0901 -856.6126 8.0866 -639.5266 14.99% 100.0780 3.0871 15.00% 100.0000 -779.8264 73.6287 3.0501 -369.9550 9,503.3302 15.01% 99.9221 -779.0901 3.0134 -367.0564 5.99% 92.6322 0.7003 16.00% 92.5613 -709.8187 71.7854 0.6879 -124.4984 25,627.6335 16.01% 92.4903 -709.1542 0.6756 -122.7355 LN03: Duration & convexity 32