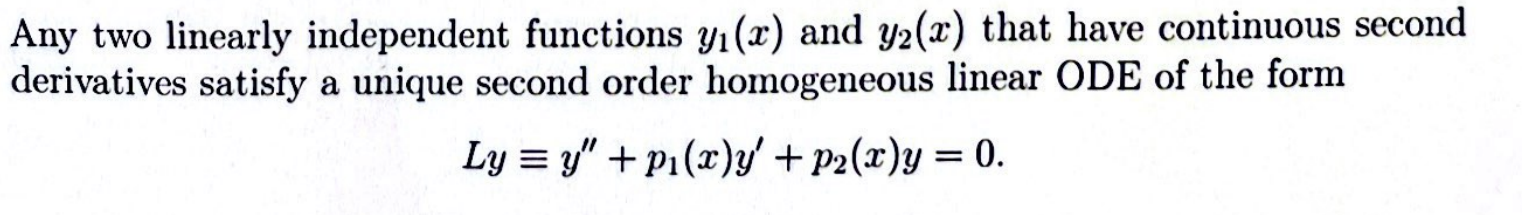
Any two linearly independent functions y(x) and y2(a) that have continuous second derivatives satisfy a unique second order homogeneous linear ODE of the form Ly=y" + pi(x)y' + p2(x)y = 0. Show that this ODE can be written in terms of a determinant as Lwy = y y' y" 31 3 3 1 = 0. yi Y y Y2 Y2 Y2 There is more than one way of showing this. One way is to find the functions p(x) and p2(x) in terms of y(x) and y2(x). There is a simpler approach that uses the form of the general solution and a basic result from linear algebra. The result can be extended to n linearly independent functions {y(x), ..., Yn(x)} that satisfy an nth order ODE which can be expressed as a determinant. What would you expect the result to be? (5 points)