approaching deadline please answer it ASAP
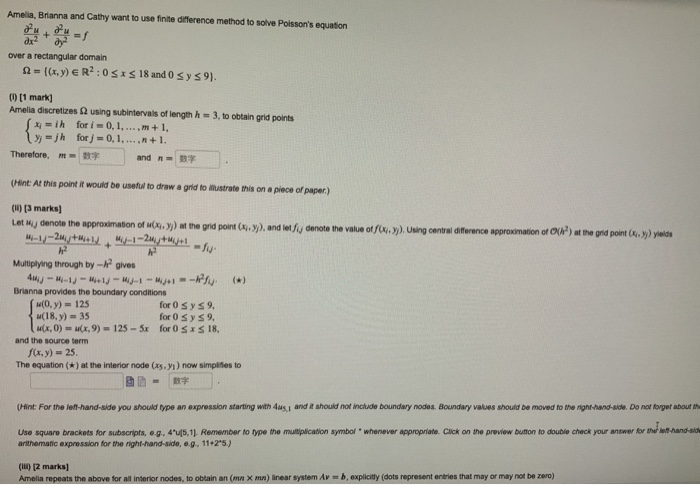
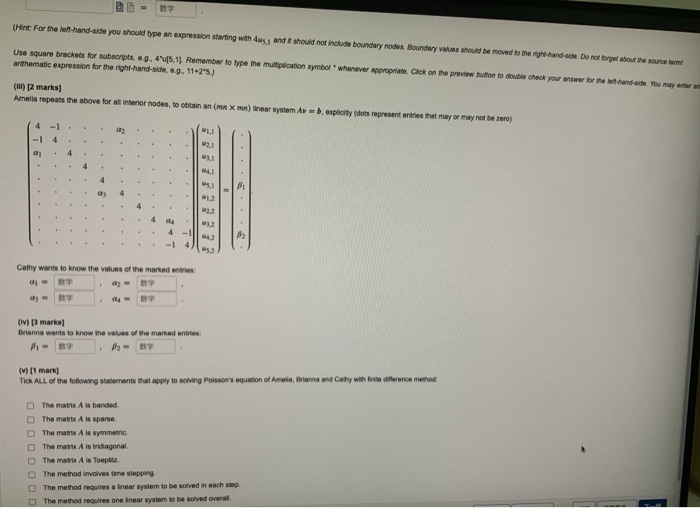
Amelia, Brianna and Cathy want to use finite difference method to solve Poisson's equation + over a rectangular domain 12 {(x,y) ER?:05xs 18 and 0 Sys 9). [1 mark] Amelia discretizes using subintervals of length h 3. to obtain grid points x=ih for i0,1,...,m+ 1 Uy-jh for j = 0,1,...,n+ 1. Therefore, and (Hint: At this point it would be useful to draw a grid to llustrate this on a piece of paper) () [3 marks] Let My denote the approximation of u(xy)) at the grid point (.)), and let y denote the value of xv.)). Using central difference approximation of ow) at the pred point (.)) yields -1/-20/+*+M-1 -2/+/+1 Multiplying through by - gives 4--1 - +/- 1 - 1 - .-ks. Brianna provides the boundary conditions (Oy) - 125 for 0 Sys9. (18,y)=35 for 0 Sys9. (x,0) = (x 9) = 125 -5x for 0 SXS 18, and the source term f(x,y) - 25 The equation (*) at the interior node (xs. Y) now simplifies to (Hint: For the left-hand-side you should type an expression starting with us, and it should not include boundary nodes. Boundary values should be moved to the right hand side. Do not forget about th Use square brackets for subscripts, eg, 4"x6.1). Remember to type the multiplication symbol" whenever appropriate. Cick on the preview button to doutilo check your answer for www.hand side arithematic expression for the right-hand side, e.g. 11-25) (II) [2 marks] Amelia repeats the above for all interior nodes, to obtain an ( X ) linear system Av=b, explicitly (dots represent entries that may or may not be zero) (HintFor the left hand side you should type an expression starting with us, and it should not include boundary nodes. Boundary values should be moved to the right and side. Do not forget about the source form Use square brackets for subscripts...425.11. Remember to type the multiplication symbol whenever appropriate. Click on the preview button to double check your answer for the hand side. You may arter arthematic expression for the night-hand-side, eg. 11-25) (1) 12 marks] Amella repeat the above for all interior nodes to obtain an ( mm) linear syster Av = esplicity dots represent entries that may or may not be ero) - 4 2.1 M M2 04 P2 -14 2 Cathy wants to know the values of the marked entries - (v) marks] Brianna wants to know the values of the marked entries: P-BY (1 marki Tick ALL of the following statements that apply to solving Poisson's equation of Amelia, Brianna and Cathy with fine difference method The matrix A is banded The matrix A is sparse The matrix A is symmetrie The matrix A is tridiagonal The matrix Ais Toeplice The method involves time stepping The method requires a linear system to be solved in each step The method requires one linear system to be solved overall Amelia, Brianna and Cathy want to use finite difference method to solve Poisson's equation + over a rectangular domain 12 {(x,y) ER?:05xs 18 and 0 Sys 9). [1 mark] Amelia discretizes using subintervals of length h 3. to obtain grid points x=ih for i0,1,...,m+ 1 Uy-jh for j = 0,1,...,n+ 1. Therefore, and (Hint: At this point it would be useful to draw a grid to llustrate this on a piece of paper) () [3 marks] Let My denote the approximation of u(xy)) at the grid point (.)), and let y denote the value of xv.)). Using central difference approximation of ow) at the pred point (.)) yields -1/-20/+*+M-1 -2/+/+1 Multiplying through by - gives 4--1 - +/- 1 - 1 - .-ks. Brianna provides the boundary conditions (Oy) - 125 for 0 Sys9. (18,y)=35 for 0 Sys9. (x,0) = (x 9) = 125 -5x for 0 SXS 18, and the source term f(x,y) - 25 The equation (*) at the interior node (xs. Y) now simplifies to (Hint: For the left-hand-side you should type an expression starting with us, and it should not include boundary nodes. Boundary values should be moved to the right hand side. Do not forget about th Use square brackets for subscripts, eg, 4"x6.1). Remember to type the multiplication symbol" whenever appropriate. Cick on the preview button to doutilo check your answer for www.hand side arithematic expression for the right-hand side, e.g. 11-25) (II) [2 marks] Amelia repeats the above for all interior nodes, to obtain an ( X ) linear system Av=b, explicitly (dots represent entries that may or may not be zero) (HintFor the left hand side you should type an expression starting with us, and it should not include boundary nodes. Boundary values should be moved to the right and side. Do not forget about the source form Use square brackets for subscripts...425.11. Remember to type the multiplication symbol whenever appropriate. Click on the preview button to double check your answer for the hand side. You may arter arthematic expression for the night-hand-side, eg. 11-25) (1) 12 marks] Amella repeat the above for all interior nodes to obtain an ( mm) linear syster Av = esplicity dots represent entries that may or may not be ero) - 4 2.1 M M2 04 P2 -14 2 Cathy wants to know the values of the marked entries - (v) marks] Brianna wants to know the values of the marked entries: P-BY (1 marki Tick ALL of the following statements that apply to solving Poisson's equation of Amelia, Brianna and Cathy with fine difference method The matrix A is banded The matrix A is sparse The matrix A is symmetrie The matrix A is tridiagonal The matrix Ais Toeplice The method involves time stepping The method requires a linear system to be solved in each step The method requires one linear system to be solved overall