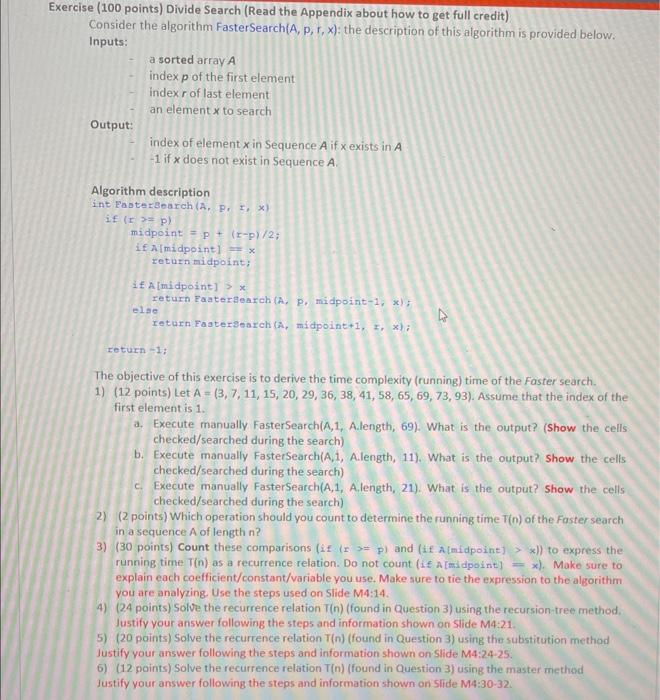
arcise ( 100 points) Divide Search (Read the Appendix about how to get full credit) Consider the algorithm FasterSearch (A,p,r,x) : the description of this algorithm is provided below. Inputs: - a sorted array A - index p of the first element - index r of last element an element x to search Output: index of element x in sequence A if x exists in A 1 if x does not exist in Sequence A. Algorithm description int PasterBearch (A, P,I,x ) if (r)=p ) midpoint =p+(rp)/2; if N[ midpoint ]=x return midpoint; if A [midpoint ]>x returh Faatergearch (A,P, midpoint-1, x); elae return Faatereoarch (A, midpoint +1,2,x); return -1; The objective of this exercise is to derive the time complexity (running) time of the Faster search. 1) (12 points) Let A=(3,7,11,15,20,29,36,38,41,58,65,69,73,93). Assume that the index of the first element is 1. a. Execute manually FasterSearch(A,1, A.length, 69). What is the output? (Show the cells checked/searched during the search) b. Execute manually FasterSearch(A,1, A.length, 11). What is the output? Show the cells checked/searched during the search) c. Execute manually FasterSearch(A,1, A.length, 21). What is the output? Show the cells checked/searched during the search) 2) (2 points) Which operation should you count to determine the running time T(n) of the Faster search in a sequence A of length n ? 3) (30 points) Count these comparisons (if (r>=p) and (if A imidpoint )>x) ) to express the running time T(n) as a recurrence relation. Do not count (if A [midpoint] =x ). Make sure to explain each coefficient/constant/variable you use. Make sure to tie the expression to the algorithm you are analyzing. Use the steps used on Slide M4:14. 4) (24 points) Solve the recurrence relation T(n) (found in Question 3) using the recursion-tree method, Justify your answer following the steps and information shown on slide M4:21. 5) (20 points) Solve the recurrence relation T(n) (found in Question 3) using the substitution method Justify your answer following the steps and information shown on slide M4:24-25. 6) (12 points) Solve the recurrence relation T(n) (found in Question 3) using the master methisd Justify your answer following the steps and information shown on slide M4:30-32