Are there any mistakes with my Plot?

I need to duplicate this plot: 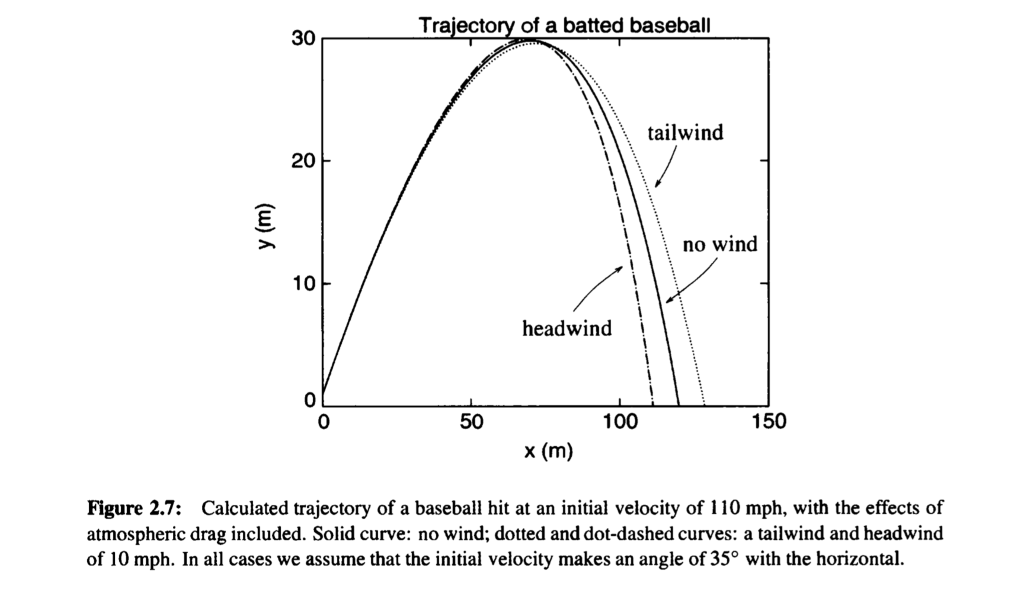I'm pretty confident I did my code correctly. But the landing points for my baseball with a headwind and with a tail wind seem to be a bit closer and a bit farther than the one from the textbook.

Here is my code:

%x() and y() are the positions of the projectile

%dt = time step

%v_init = initial speed

%theta = launch angle

%B_m = proportional to drag force = B2/m

close all

clear all

clc

%define Variables and Matrices

timeStep = .001;

initialPositionX = 0;

initialPositionY = 1;

initialVelocity = 110*0.44704; %mph to m/s

positionXNoWind = zeros(1,50);

positionYNoWind = zeros(1,50);

positionXNoWind(1) = initialPositionX;

positionYNoWind(1) = initialPositionY;

theta = 36 * 0.0174533; %degrees to radians

initialVelocityX = initialVelocity * cos(theta);

initialVelocityY = initialVelocity * sin(theta);

vd = 35; %m/s

delta = 5; %m/s

gravity = -9.8;

maxCalculations=100000000;

Bm = .0039 + (.0058)/(1+exp((initialVelocity-vd)/delta)); %B2/m

velocity = initialVelocity;

velocityX = initialVelocityX;

velocityY = initialVelocityY;

velocityWind = 0 * 0.44704; %mph to m/s

for i = 2:maxCalculations

positionXNoWind(i) = positionXNoWind(i-1) + velocityX * timeStep;

positionYNoWind(i) = positionYNoWind(i-1) + velocityY * timeStep;

velocity = sqrt(velocityX^2 + velocityY^2);

Bm = .0039 + (.0058)/(1+exp((velocity-vd)/delta));

dragForceX = Bm * (velocity - velocityWind);

dragForceY = Bm * (velocity);

velocityY = velocityY - (9.8 * timeStep) - (dragForceY * velocityY * timeStep);

velocityX = velocityX - (dragForceX * (velocityX - velocityWind) * timeStep);

%positionX(i) = positionX(i-1) + velocityX * timeStep

%positionY(i) = positionY(i-1) + velocityY * timeStep

%velocityY = velocityY - (9.8 * timeStep) - (dragForce * velocityY * timeStep)

%velocityX = velocityX - (dragForce * velocityX * timeStep)

%initialVelocity = sqrt(initialVelocityX^2 + initialVelocityY^2)

%positionX(i) = positionX(i-1) + (velocityX - (dragForce * velocityX * timeStep)) * timeStep

%positionY(i) = positionY(i-1) + (velocityY - (9.8 * timeStep) - (dragForce * velocityY * timeStep)) * timeStep

%Bm = .0039 + (.0058)/(1+exp((velocity-vd)/delta))

if positionYNoWind(i)

break

end

end

positionXTailWind = zeros(1,50);

positionYTailWind = zeros(1,50);

positionXTailWind(1) = initialPositionX;

positionYTailWind(1) = initialPositionY;

velocity = initialVelocity;

velocityX = initialVelocityX;

velocityY = initialVelocityY;

velocityWind = 10 * 0.44704; %mph to m/s

for i = 2:maxCalculations

positionXTailWind(i) = positionXTailWind(i-1) + velocityX * timeStep;

positionYTailWind(i) = positionYTailWind(i-1) + velocityY * timeStep;

velocity = sqrt(velocityX^2 + velocityY^2);

Bm = .0039 + (.0058)/(1+exp((velocity-vd)/delta));

dragForceX = Bm * (velocity - velocityWind);

dragForceY = Bm * (velocity);

velocityY = velocityY - (9.8 * timeStep) - (dragForceY * velocityY * timeStep);

velocityX = velocityX - (dragForceX * (velocityX - velocityWind) * timeStep);

%positionX(i) = positionX(i-1) + velocityX * timeStep

%positionY(i) = positionY(i-1) + velocityY * timeStep

%velocityY = velocityY - (9.8 * timeStep) - (dragForce * velocityY * timeStep)

%velocityX = velocityX - (dragForce * velocityX * timeStep)

%initialVelocity = sqrt(initialVelocityX^2 + initialVelocityY^2)

%positionX(i) = positionX(i-1) + (velocityX - (dragForce * velocityX * timeStep)) * timeStep

%positionY(i) = positionY(i-1) + (velocityY - (9.8 * timeStep) - (dragForce * velocityY * timeStep)) * timeStep

%Bm = .0039 + (.0058)/(1+exp((velocity-vd)/delta))

if positionYTailWind(i)

break

end

end

positionXHeadWind = zeros(1,50);

positionYHeadWind = zeros(1,50);

positionXHeadWind(1) = initialPositionX;

positionYHeadWind(1) = initialPositionY;

velocity = initialVelocity;

velocityX = initialVelocityX;

velocityY = initialVelocityY;

velocityWind = -10 * 0.44704; %mph to m/s

for i = 2:maxCalculations

positionXHeadWind(i) = positionXHeadWind(i-1) + velocityX * timeStep;

positionYHeadWind(i) = positionYHeadWind(i-1) + velocityY * timeStep;

velocity = sqrt(velocityX^2 + velocityY^2);

Bm = .0039 + (.0058)/(1+exp((velocity-vd)/delta));

dragForceX = Bm * (velocity - velocityWind);

dragForceY = Bm * velocity;

velocityY = velocityY - (9.8 * timeStep) - (dragForceY * velocityY * timeStep);

velocityX = velocityX - (dragForceX * (velocityX - velocityWind) * timeStep);

%positionX(i) = positionX(i-1) + velocityX * timeStep

%positionY(i) = positionY(i-1) + velocityY * timeStep

%velocityY = velocityY - (9.8 * timeStep) - (dragForce * velocityY * timeStep)

%velocityX = velocityX - (dragForce * velocityX * timeStep)

%initialVelocity = sqrt(initialVelocityX^2 + initialVelocityY^2)

%positionX(i) = positionX(i-1) + (velocityX - (dragForce * velocityX * timeStep)) * timeStep

%positionY(i) = positionY(i-1) + (velocityY - (9.8 * timeStep) - (dragForce * velocityY * timeStep)) * timeStep

%Bm = .0039 + (.0058)/(1+exp((velocity-vd)/delta))

if positionYHeadWind(i)

break

end

end

%a = -positionY(i) / positionY(i-1)

%positionX(i) = (positionX(i) + (a * positionX(i-1))) / (1 + a)

%positionY(i) = 0

%%Plots

figure(1)

hold on

box on

plot(positionXNoWind,positionYNoWind,'-k',positionXTailWind,positionYTailWind,':k',positionXHeadWind,positionYHeadWind,'-.k')

set(gca,'Xtick',linspace(0,150,31),'fontsize',18,'Ytick',linspace(0,50,6))

set(gcf,'Color','w');

set(gcf,'Resize','on');

ylim([0 30])

xlim([0 150])

hold off

Trajectory of a batted basebal 30 tailwind 20 no wind 10 headwind 0 0 50 100 150 x (m) Figure 2.7: Calculated trajectory of a baseball hit at an initial velocity of 110 mph, with the effects of atmospheric drag included. Solid curve: no wind; dotted and dot-dashed curves: a tailwind and headwind of 10 mph. In all cases we assume that the initial velocity makes an angle of 35 with the horizontal. Trajectory of a batted basebal 30 tailwind 20 no wind 10 headwind 0 0 50 100 150 x (m) Figure 2.7: Calculated trajectory of a baseball hit at an initial velocity of 110 mph, with the effects of atmospheric drag included. Solid curve: no wind; dotted and dot-dashed curves: a tailwind and headwind of 10 mph. In all cases we assume that the initial velocity makes an angle of 35 with the horizontal