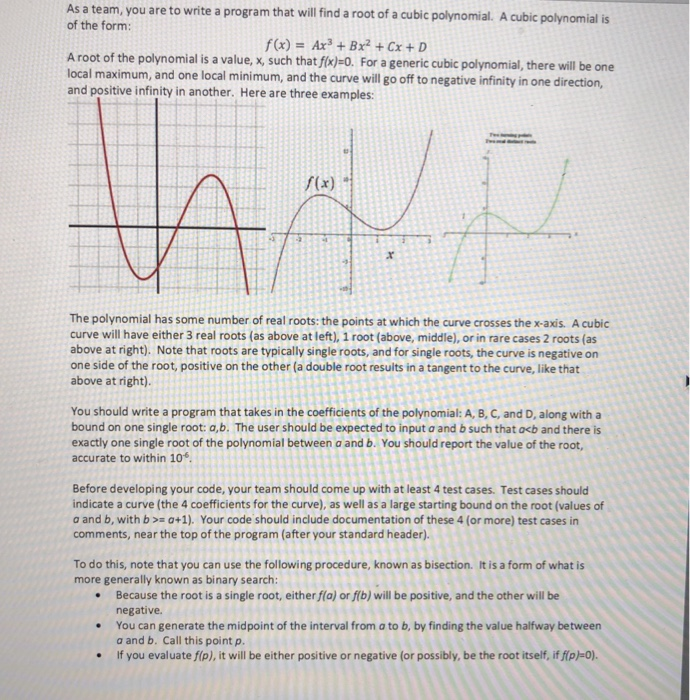
As a team, you are to write a program that will find a root of a cubic polynomial. A cubic polynomial i of the form: f(x)-Ax3 +Bx2 +Cx + D A root of the polynomial is a value, x, such that f(x)-o For a generic cubic polynomial, there will be one local maximum, and one local minimum, and the curve will go off to negative infinity in one direction and positive infinity in another. Here are three examples f(x) The polynomial has some number of real roots: the points at which the curve crosses the x-axis. A cubic curve will have either 3 real roots (as above at left), 1 root (above, middle), or in rare cases 2 roots (as above at right). Note that roots are typically single roots, and for single roots, the curve is negative on one side of the root, positive on the other (a double root results in a tangent to the curve, like that above at right). You should write a program that takes in the coefficients of the polynomial: A, B, C, and D, along witha bound on one single root: a,b. The user should be expected to input a and b such that ocb and there is exactly one single root of the polynomial between a and b. You should report the value of the root, accurate to within 1o. Before developing your code, your team should come up with at least 4 test cases. Test cases should indicate a curve (the 4 coefficients for the curve), as well as a large starting bound on the root (values of o and b, with bo+1). Your code should include documentation of these 4 (or more) test cases in comments, near the top of the program (after your standard header). To do this, note that you can use the following procedure, known as bisection. It is a form of what is more generally known as binary search: .Because the root is a single root, either fa) or fib) will be positive, and the other will be negative. .You can generate the midpoint of the interval from a to b, by finding the value halfway betweer a and b. Call this point p. .If you evaluate f(p), it will be either positive or negative (or possibly, be the root itself, if fip)-0) This will enable you to narrow the interval to either [a,p] or to [p,b]. . You can continue doing this until your interval is less than 10 wide. As a team, you should create a program that performs bisection to determine the root. More specifically, your program should do the following: . Read in the coefficients of the polynomial from the user .Read in the upper and lower bounds around a single root of the polynomial . Determine the value of that root to within 10 . Print the result of that root finding, as a single number Print out how many iterations it took to find that root. Be sure to include comments in your code. Challenge: Cubic polynomials always have one root that can be found through bisection. There also are ways to find maximum and minimum bounds on the sizes of real roots of polynomials (you will need to research this). Modify your program so that it takes in only the coefficients of the polynomial, and reports one of the real roots to within 10