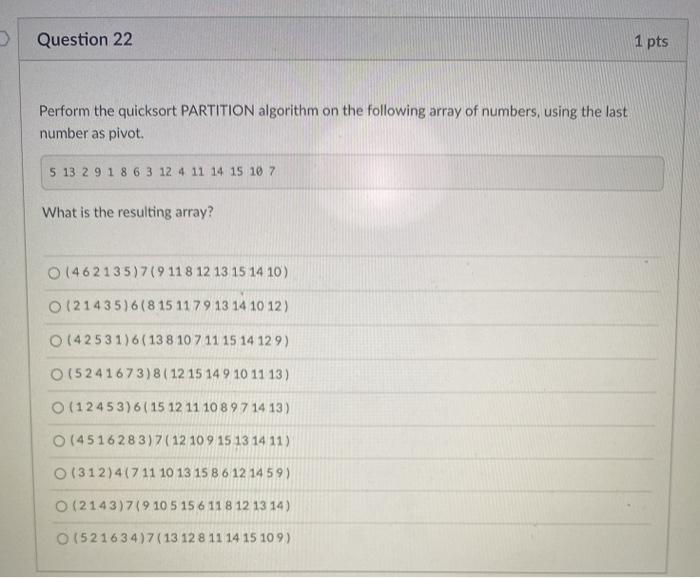
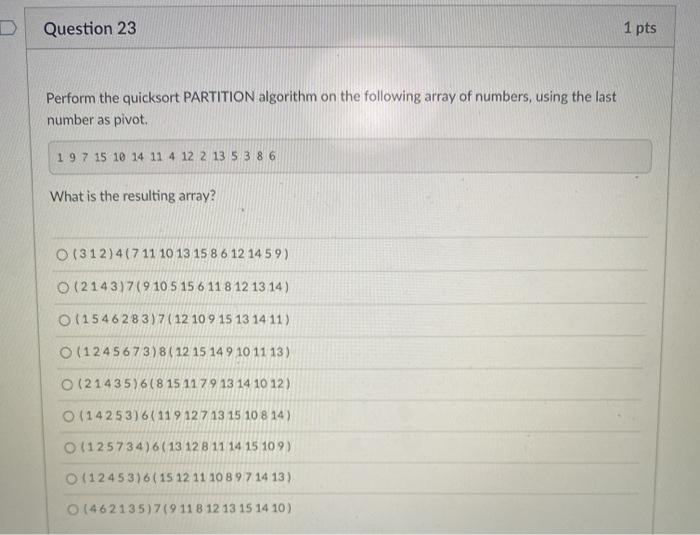
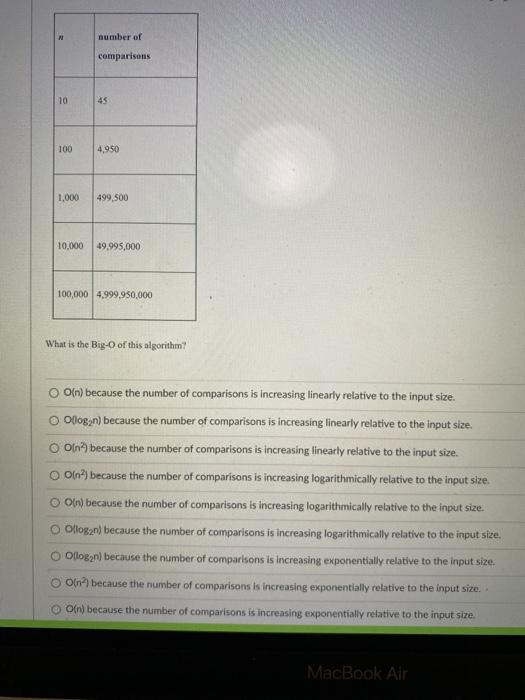
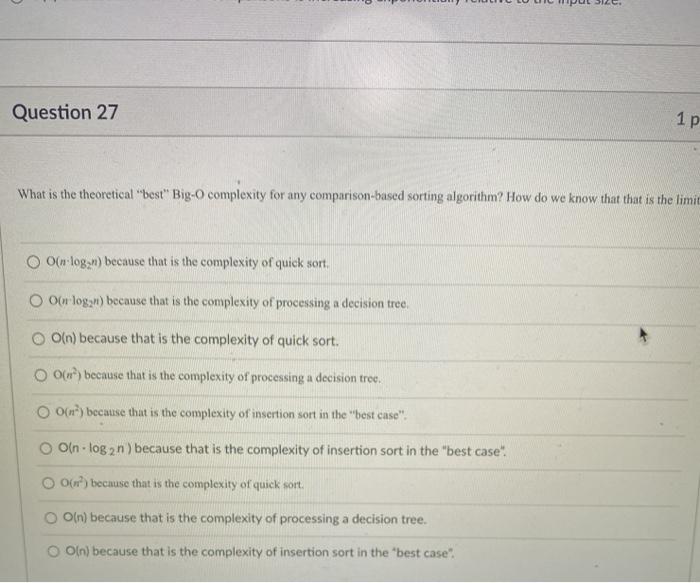
ASAP help to answer these questions, i would give a like quickly when you done with all of them asap

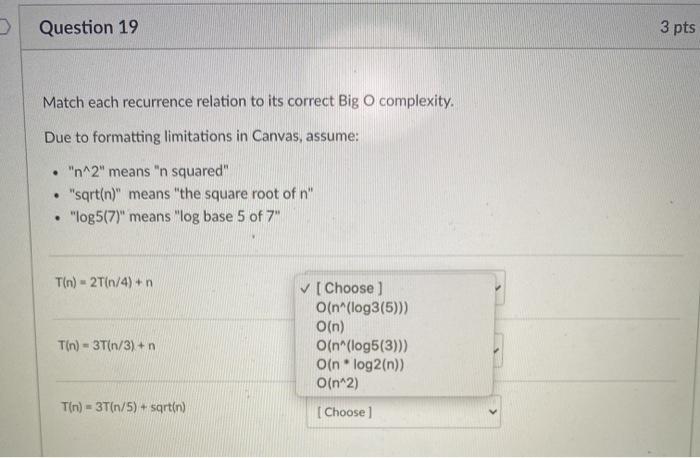
Question 19 3 pts Match each recurrence relation to its correct Big O complexity. Due to formatting limitations in Canvas, assume: "n^2" means "n squared" "sqrt(n)" means "the square root of n" "log5(7)" means "log base 5 of 7" . . T(n) = 2T(1/4) + [Choose) O(n^(log3(5))) O(n) O(n^(log5(3))) O(n * log(n)) O(n^2) T(n) = 3T(n/3) + n T(n) = 3T(n/5)+sqrt(n) [Choose Question 22 1 pts Perform the quicksort PARTITION algorithm on the following array of numbers, using the last number as pivot. 5 13 2 9 1 8 6 3 12 4 11 14 15 10 7 What is the resulting array? O (462135) 7(9 118 12 13 15 14 10) O (21435)6(8 15 1179 13 14 10 12) O(42531)6( 13 8 10 7 11 15 14 129) (5241673) 8 ( 12 15 14 9 10 11 13) (12453) 6( 15 12 11 10 8 9 7 14 13 ) (4516283)7 ( 12 10 9 15 13 14 11 ) (312)4(711 10 13 15 8 6 12 14 59) (2143) 7( 9 10 5 15 6 11 8 12 13 14 ) (52 1634)7( 13 12 8 11 14 15 109) Question 23 1 pts Perform the quicksort PARTITION algorithm on the following array of numbers, using the last number as pivot. 1 9 7 15 10 14 11 4 12 2 13 5 3 8 6 What is the resulting array? O (312) 4(711 10 13 15 8 6 12 1459) O (2143) 7( 9 10 5 15 6 11 8 12 13 14) O (1546283) 7 ( 12 10 9 15 13 14 11) O (1245673) 8 ( 12 15 14 9 10 11 13) O (21 435)6(8 15 1179 13 14 10 12) O (14253) 6( 119 127 13 15 10 8 14) (125734) 6( 13 12 8 11 14 15 109) (12453)6( 15 12 11 10 8 9 7 14 13) (462135)7(9 118 1213 15 14 10) number of comparisons 10 45 100 4,950 1.000 499,500 10,000 49.995,000 100,000 4,999,950,000 What is the Big-O of this algorithm O Oln) because the number of comparisons is increasing linearly relative to the input size. Ollogn) because the number of comparisons is increasing linearly relative to the input size. oo) because the number of comparisons is increasing linearly relative to the input size. Ol) because the number of comparisons is increasing logarithmically relative to the input size. om) because the number of comparisons is increasing logarithmically relative to the input size. Ollogen) because the number of comparisons is increasing logarithmically relative to the input size. Ollogar) because the number of comparisons is increasing exponentially relative to the input size. On because the number of comparisons is increasing exponentially relative to the input size.. O(n) because the number of comparisons is increasing exponentially relative to the input size MacBook Air Question 27 1 1 p What is the theoretical "best" Big-O complexity for any comparison-based sorting algorithm? How do we know that that is the limit O(log,n) because that is the complexity of quick sort, OOorlog20) because that is the complexity of processing a decision tree, O O(n) because that is the complexity of quick sort. O 0(?) because that is the complexity of processing a decision tree. (?) because that is the complexity of insertion sort in the best case". Oln. log 2n) because that is the complexity of insertion sort in the "best case". OO() because that is the complexity of quick sort, O(n) because that is the complexity of processing a decision tree. O Oln) because that is the complexity of insertion sort in the best case