% assemble element stiffness matrix

function K = assembly(K,e,ke)

include_flags;

for loop1 = 1:nen*ndof

i = LM(loop1,e);

for loop2 = 1:nen*ndof

j = LM(loop2,e);

K(i,j) = K(i,j) + ke(loop1,loop2);

end

end

% file to include global variables

global nsd ndof nnp nel nen neq nd

global CArea E leng phi

global plot_truss plot_nod plot_stress

global LM IEN x y stress

% In class example based on problem 2.8-book

nsd = 2; % Number of space dimensions

ndof = 2; % Number of degrees-of-freedom per node

nnp = 8; % Number of nodal points

nel = 12; % Number of elements

nen = 2; % Number of nodes/ element

neq = ndof*nnp; % Number of equations

f = zeros(neq,1); % Initialize force vector

d = zeros(neq,1); % Initialize displacement matrix

K = zeros(neq); % Initialize stiffness matrix

%

flags = zeros(neq,1); % Initializeflags = zeros(neq,1); % Initialize flags

e_bc = zeros(neq,1); % Initializee-bc = zeros(neq,1); % Initialize flags

n_bc = zeros(neq,1); % Initializee-n-bc = zeros(neq,1); % Initialize flags

% Element properties

CArea = 2*[1 1 1 1 1 1 1 1 1 1 1 1]; % Elements area

E = 30e6*[1 1 1 1 1 1 1 1 1 1 1 1]; % Youngs Modulus

% % flags for forces and prescribed disp.

flags(15)=0;% horizontal force in node 2

flags(9:14)=3000; % Vertical Force

flags(7:8)=20; % pins ins nodes 3-5

n_bc(3)=30; %magnitude of force in dof 3

e_bc(15)=0; %magnitude of known displacements

% output plots

plot_truss = 'yes';

plot_nod = 'yes';

% mesh Generation

truss_mesh;

% function to plot the elements, global node numbers and print mesh parameters

function plotdisp(d)

include_flags;

% check if truss plot is requested

if strcmpi(plot_truss,'yes')==1;

for i = 1:nel

XX = [x(IEN(1,i)) x(IEN(2,i)) ];

YY = [y(IEN(1,i)) y(IEN(2,i)) ];

line(XX,YY);hold on;

mag=1e10; %magnification factor

%to visualize disp.

dx1=mag*d(IEN(1,i)*2-1);% dof in x of node 1

dx2=mag*d(IEN(2,i)*2-1);% dof in x of node 1

dy1=mag*d(IEN(1,i)*2);% dof in y of node 1

dy2=mag*d(IEN(2,i)*2);% dof in y of node 1

XX = [x(IEN(1,i))+dx1 x(IEN(2,i))+dx2];

YY = [y(IEN(1,i))+dy1 y(IEN(2,i))+dy2];

plot(XX,YY,'--r');hold on;

% check if node numbering is requested

if strcmpi(plot_nod,'yes')==1;

text(XX(1),YY(1),sprintf('%0.5g',IEN(1,i)));

text(XX(2),YY(2),sprintf('%0.5g',IEN(2,i)));

end

end

title('Truss Plot');

end

% print mesh parameters

fprintf(1,'\tTruss Params ');

fprintf(1,'No. of Elements %d ',nel);

fprintf(1,'No. of Nodes %d ',nnp);

fprintf(1,'No. of Equations %d ',neq);

% function to plot the elements, global node numbers and print mesh parameters

function plottruss

include_flags;

% check if truss plot is requested

if strcmpi(plot_truss,'yes')==1;

for i = 1:nel

XX = [x(IEN(1,i)) x(IEN(2,i)) ];

YY = [y(IEN(1,i)) y(IEN(2,i)) ];

line(XX,YY);hold on;

% check if node numbering is requested

if strcmpi(plot_nod,'yes')==1;

text(XX(1),YY(1),sprintf('%0.5g',IEN(1,i)));

text(XX(2),YY(2),sprintf('%0.5g',IEN(2,i)));

end

end

title('Truss Plot');

end

% print mesh parameters

fprintf(1,'\tTruss Params ');

fprintf(1,'No. of Elements %d ',nel);

fprintf(1,'No. of Nodes %d ',nnp);

fprintf(1,'No. of Equations %d ',neq);

% function to plot the elements, global node numbers and print mesh parameters

function plottruss

include_flags;

% check if truss plot is requested

if strcmpi(plot_truss,'yes')==1;

for i = 1:nel

XX = [x(IEN(1,i)) x(IEN(2,i)) ];

YY = [y(IEN(1,i)) y(IEN(2,i)) ];

line(XX,YY);hold on;

% check if node numbering is requested

if strcmpi(plot_nod,'yes')==1;

text(XX(1),YY(1),sprintf('%0.5g',IEN(1,i)));

text(XX(2),YY(2),sprintf('%0.5g',IEN(2,i)));

end

end

title('Truss Plot');

end

% print mesh parameters

fprintf(1,'\tTruss Params ');

fprintf(1,'No. of Elements %d ',nel);

fprintf(1,'No. of Nodes %d ',nnp);

fprintf(1,'No. of Equations %d ',neq);

% postprocessing function

function postprocessor(d)

include_flags;

% prints the element numbers and corresponding stresses

fprintf(1,'element\t\t\tstress ');

% compute stress vector

for e=1:nel

de = d(LM(:,e)); % displacement at the current element

const = E(e)/leng(e); % constant parameter within the element

if ndof == 1 % For 1-D truss element

stress(e) = const*([-1 1]*de);

end

if ndof == 2 % For 2-D truss element

p = phi(e)*pi/180; % Converts degrees to radians

c = cos(p); s = sin(p);

stress(e) = const*[-c -s c s]*de; % compute stresses

end

fprintf(1,'%d\t\t\t%f ',e,stress(e));

end

% preprocessing read input data and set up mesh information

function [K,f,d] = preprocessor

include_flags;

% input file to include all variables

input_file;

% generate LM array

for e = 1:nel

for j = 1:nen

for m = 1:ndof

ind = (j-1)*ndof + m;

LM(ind,e) = ndof*IEN(j,e) - ndof + m;

end

end

end

% partition and solve the system of equations

function [d,f_E] = solvedr(K,f,d)

include_flags;

% partition the matrix K, vectors f and d

K_E = K(1:nd,1:nd); % Extract K_E matrix

K_F = K(nd+1:neq,nd+1:neq); % Extract K_E matrix

K_EF = K(1:nd,nd+1:neq); % Extract K_EF matrix

f_F = f(nd+1:neq); % Extract f_F vector

d_E = d(1:nd); % Extract d_E vector

% solve for d_F

d_F =K_F\( f_F - K_EF'* d_E);

% reconstruct the global displacement d

d = [d_E

d_F];

% compute the reaction r

f_E = K_E*d_E+K_EF*d_F;

% write to the workspace

solution_vector_d = d

reactions_vector = f_E

% geometry and connectivity for example problem in Figure 2.8

function truss_mesh

include_flags;

% Nodal coordinates (origin placed at node 4)

x = [ 1 4 0 2 4 ]; % x coordinate

y = [ 1.73205078 2 0 0 0]; % y coordinate

% connectivity array

IEN = [3 4 1 4 5

1 1 2 2 2 ];

for i=1:nel

x1=x(IEN(1,i)); % x value of node 1

x2=x(IEN(2,i)); % x value of node 2

y1=y(IEN(1,i)); % y value of node 1

y2=y(IEN(2,i)); % y value of node 2

leng(i)=sqrt((x2-x1)^2+(y2-y1)^2);%length of el

phi(i)=acosd((x2-x1)/leng(i));

end

plottruss;

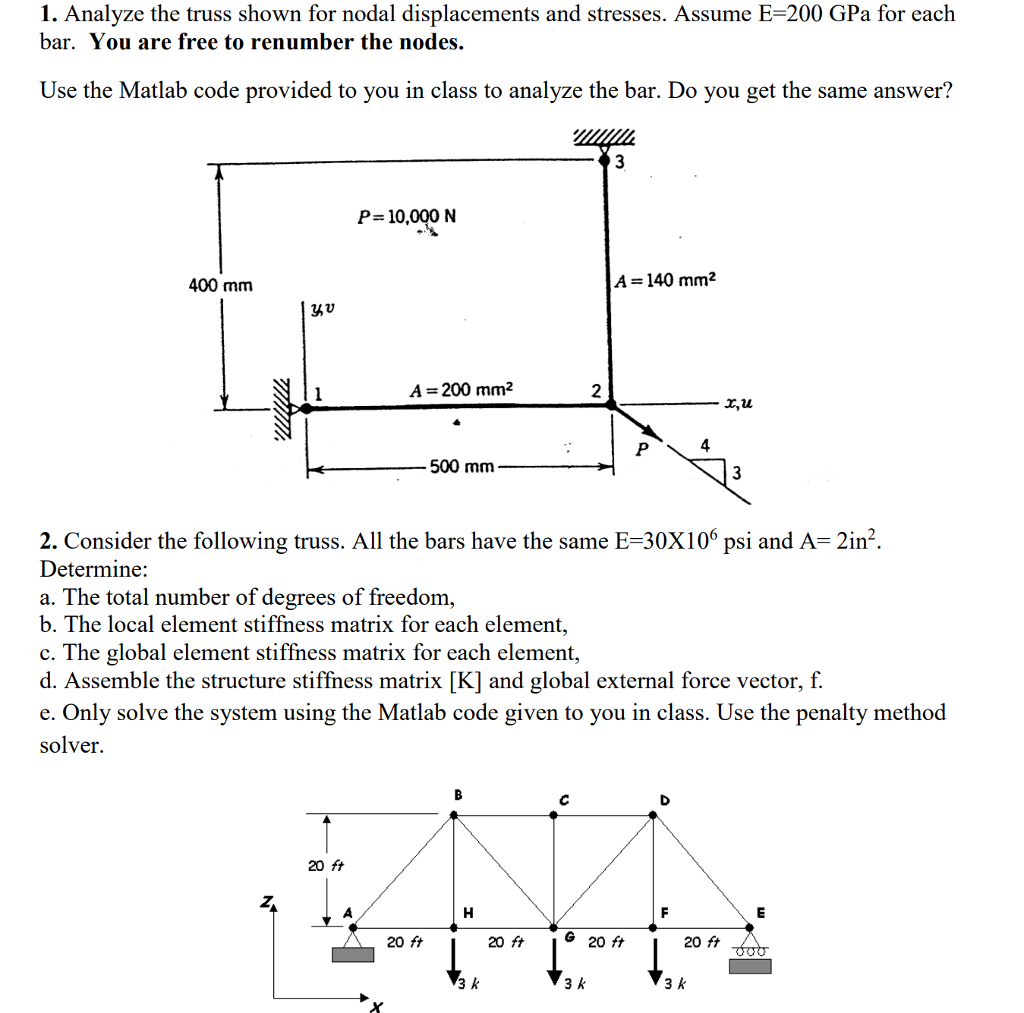
PLEASE SOLVE NUMBER 2 WITH THE CODE GIVEN BELOW> JUST HAVE TO FILL IN THE BLANKS WITH PROPPER FORCES

1. Analyze the truss shown for nodal displacements and stresses. Assume E-200 GPa for each bar. You are free to renumber the nodes. Use the Matlab code provided to you in class to analyze the bar. Do you get the same answer? P= 10,000 N 400 mm A-140 mm2 yyu A 200 mm2 2 x,u 4. 500 mm 3 2. Consider the following truss. All the bars have the same E-30X106 psi and A- 2in2 Determine: a. The total number of degrees of freedom b. The local element stiffness matrix for each element, c. The global element stiffness matrix for each element, d. Assemble the structure stiffness matrix [K] and global external force vector, f. e. Only solve the system using the Matlab code given to you in class. Use the penalty method solver. 20 ft 20 ft 20 ft G 20 ft 20 ft 3 k 3 k 3 k 1. Analyze the truss shown for nodal displacements and stresses. Assume E-200 GPa for each bar. You are free to renumber the nodes. Use the Matlab code provided to you in class to analyze the bar. Do you get the same answer? P= 10,000 N 400 mm A-140 mm2 yyu A 200 mm2 2 x,u 4. 500 mm 3 2. Consider the following truss. All the bars have the same E-30X106 psi and A- 2in2 Determine: a. The total number of degrees of freedom b. The local element stiffness matrix for each element, c. The global element stiffness matrix for each element, d. Assemble the structure stiffness matrix [K] and global external force vector, f. e. Only solve the system using the Matlab code given to you in class. Use the penalty method solver. 20 ft 20 ft 20 ft G 20 ft 20 ft 3 k 3 k 3 k