Question
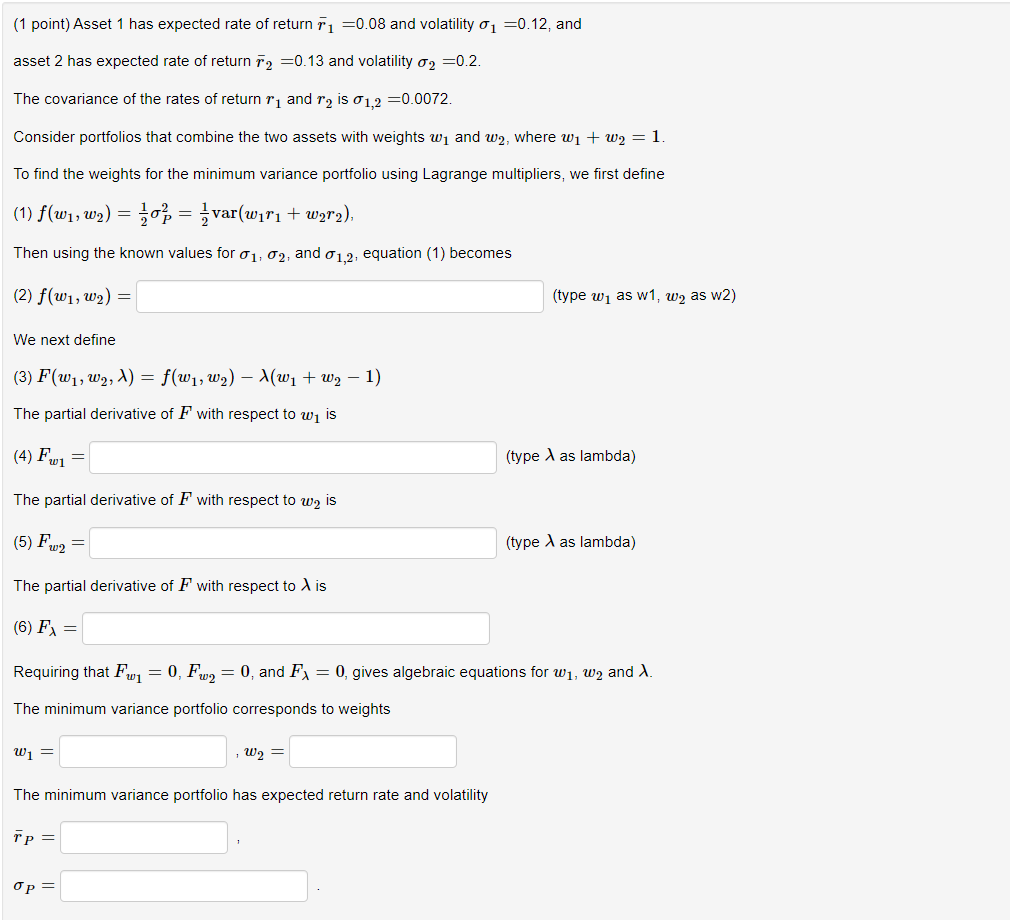
Asset 1 has expected rate of return r1=r1=0.08 and volatility 1=1=0.12, and asset 2 has expected rate of return r2=r2=0.13 and volatility 2=2=0.2. The covariance
Asset 1 has expected rate of return r1=r1=0.08 and volatility 1=1=0.12, and
asset 2 has expected rate of return r2=r2=0.13 and volatility 2=2=0.2.
The covariance of the rates of return r1r1 and r2r2 is 1,2=1,2=0.0072.
Consider portfolios that combine the two assets with weights w1w1 and w2w2, where w1+w2=1w1+w2=1.
To find the weights for the minimum variance portfolio using Lagrange multipliers, we first define
(1) f(w1,w2)=122P=12var(w1r1+w2r2)f(w1,w2)=12P2=12var(w1r1+w2r2),
Then using the known values for 11, 22, and 1,21,2, equation (1) becomes
(2) f(w1,w2)=f(w1,w2)= (type w1w1 as w1, w2w2 as w2)
We next define
(3) F(w1,w2,)=f(w1,w2)(w1+w21)F(w1,w2,)=f(w1,w2)(w1+w21)
The partial derivative of FF with respect to w1w1 is
(4) Fw1=Fw1= (type as lambda)
The partial derivative of FF with respect to w2w2 is
(5) Fw2=Fw2= (type as lambda)
The partial derivative of FF with respect to is
(6) F=F=
Requiring that Fw1=0Fw1=0, Fw2=0Fw2=0, and F=0F=0, gives algebraic equations for w1w1, w2w2 and .
The minimum variance portfolio corresponds to weights
w1=w1= , w2=w2=
The minimum variance portfolio has expected return rate and volatility
rP=rP= ,
P=P= .
Step by Step Solution
There are 3 Steps involved in it
Step: 1

Get Instant Access to Expert-Tailored Solutions
See step-by-step solutions with expert insights and AI powered tools for academic success
Step: 2

Step: 3

Ace Your Homework with AI
Get the answers you need in no time with our AI-driven, step-by-step assistance
Get Started


