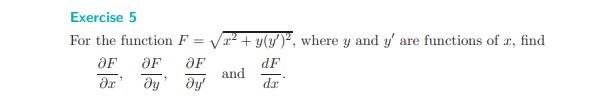Assist with the following:

Exercise 10 Consider the functional shul = [ (my' + y) dx, y(1) = In2, y(2) = In3. (a) Show that the first integral of the Euler-Lagrange equation is dy = ney, y(1) = In2, y(2) = In3, for some constant o. (b) Hence show that the stationary function is y = In(a + 1). Exercise 11 Consider the functional Stu] = ( Vy(1+ (y')?) dx, y(-1) = y(1) = A, where A > 1. (a) Show that the first integral of the Euler-Lagrange equation for this functional is y' = =vy-k2, y(-1) = y(1) = A. (b) Hence show that the functional is stationary on the paths y(x) = h+- Ah where h = =(A+ VA? - 1 ).Exercise 3 Consider the functional 2 Styl = 1 r(y')? dx, y(1) = 0, y(2) = 1. (a) Show that the stationary path satisfies ry'(a) = constant. (b) Hence show that the stationary function is y(x) = Inx/ In 2.Exercise 2 Determine the value of the functional S[yl y'(x) dr for the following functions. (a) y(x) = r (b) y(x) =1Exercise 5 For the function F = vr" +y(y'), where y and y' are functions of x, find OF OF OF dF and dy dy' dxExercise 4 Let F= xvy- + (y')?, where y and y' are functions of r. OF OF OF dF (a) Find Or ' dy and dy' and hence find dF (b) If y = sinr, then find by (i) substituting y = sin r into the formula for F and differentiating (ii) using the result from part (a).Exercise 1 Let P. = (-1,0) and P. = (1, 0). Verify the following statements. (a) If y = y(x) is the straight line joining P. to P, (i.e. the red line in Figure 4), then the functional (2) has the value Sly] = 2. (b) If y = y(x) is the upper semicircle with diameter the straight line from Pa to P (i.e. the blue curve in Figure 4), so that r' + y' = 1, then Pa P Sly] = T. -1 1 (Hint: You may assume the following standard integral, given in the Figure 4 The two paths in 1 Handbook: dex = arcsin r.) Exercise 1Exercise 7 Consider the functional Stu] = ((3)2 + y) dr, y(0) = 0, y(1) = 2. (a) Show that the stationary paths of this functional must satisfy 2y" - 1 = 0, #(0) =0, y(1) = 2. (b) Solve this differential equation to show that the stationary path is y = ta'+. Exercise 8 (a) Show that the Euler-Lagrange equation for the functional Styl = (()2 -y?) dx, y(0) =0, y(X) = 1, where 0