Assume the following:

Functional units are not pipelined.

There is no forwarding between functional units; results are communicated by the common data bus (CDB).

The execution stage (EX) does both the effective address calculation and the memory access for loads and stores. Thus, the pipeline is IF/ID/IS/EX/WB.

Loads require one clock cycle.

The issue (IS) and write-back (WB) result stages each require one clock cycle.

There are five load buffer slots and five store buffer slots.

Assume that the Branch on Not Equal to Zero (BNEZ) instruction requires one clock cycle.

For this problem use the two-issue Tomasulo MIPS pipeline with the above latencies. Show the number of stall cycles for each instruction and what clock cycle each instruction begins execution (i.e., enters its first EX cycle) for three iterations of the loop. How many cycles does each loop iteration take? Report your answer in the form of a table with the following column headers:

(1) With speculation; and assume the outcome of branch instruction is correctly predicted.

(2) Assume there is an integer ALU for address calculation; and another integer ALU for branch and all other integer operations.

(3) If the first instruction in an issue packet is a branch instruction, only this branch instruction can be issued in this cycle.

(4) Up to two instructions can be committed per cycle.

(5) There are two CDBs.

(6) For load/store, EX is for address calculation.

(7) There are twelve Reorder Buffer (ROB) entries.

(8) Only show the first two iterations and ignore the DADDIU instruction before the loop.

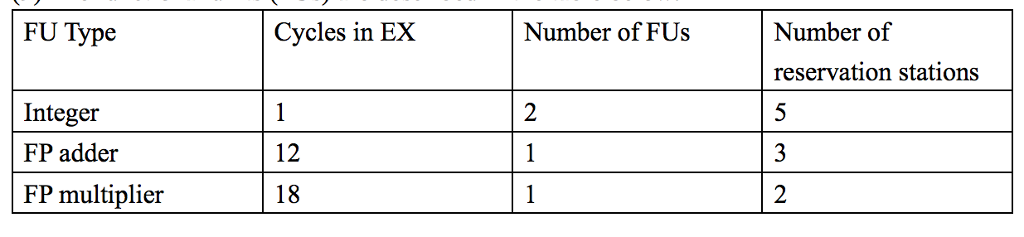
(9) The functional units (FUs) are described in the table above.

DADDIU R4,R1,#800 ; R1 = upper bound for X foo: L.D F2,0(R1) ; (F2)=x(1) MULD F4 , F2 , FO ; (F4)=a*x(1) F6 , 0 (R2) ; (F6)=Y(1) ADD . D F6, F4 , F6 ; (F6)=a*x(i) +Y(i) F6 , 0 (R2) ; Y(1) = a"X (1) + Y(1) DADDIU R1,R1,#8 ; increment X index DADDIU R2 , R2 , #8 ; increment Y index DS LTU R3,R1,R4 ;test: continue loop? BNEZ R3, foo ; loop if needed YYXXO eel nned ))iiue nd )()((XYi ))XYi e le eiXiXX te XaYaanno eecf ll ll m rrtp 12 -FFFF(nneo Yiit1 8)0)6)884 #1F2F2##R 1, R 2 R 4 R 1 2 1 O R0F0F0RRRf 4246661233 UU 11U DDTZ DDLDDDDDLE A.U D.AASN DLMLASDDDB DADDIU R4,R1,#800 ; R1 = upper bound for X foo: L.D F2,0(R1) ; (F2)=x(1) MULD F4 , F2 , FO ; (F4)=a*x(1) F6 , 0 (R2) ; (F6)=Y(1) ADD . D F6, F4 , F6 ; (F6)=a*x(i) +Y(i) F6 , 0 (R2) ; Y(1) = a"X (1) + Y(1) DADDIU R1,R1,#8 ; increment X index DADDIU R2 , R2 , #8 ; increment Y index DS LTU R3,R1,R4 ;test: continue loop? BNEZ R3, foo ; loop if needed YYXXO eel nned ))iiue nd )()((XYi ))XYi e le eiXiXX te XaYaanno eecf ll ll m rrtp 12 -FFFF(nneo Yiit1 8)0)6)884 #1F2F2##R 1, R 2 R 4 R 1 2 1 O R0F0F0RRRf 4246661233 UU 11U DDTZ DDLDDDDDLE A.U D.AASN DLMLASDDDB