Assuming you are a software analyst on a project that requires extensive (in millions) rotation of points and computation of distance between any two points and performance is key to the success of the project. However, to realize this, you are allowed to store a point either in its Polar or Cartesian coordinates formats. For example, you may choose to store a point in its Polar form but provide interfaces to convert or store it in its Cartesian form and vice-versa. In its Cartesian state, you will be storing the x and y coordinates of the point while you will be storing its distance from a reference point (r) and theta - an angle from the reference direction () in its Polar state

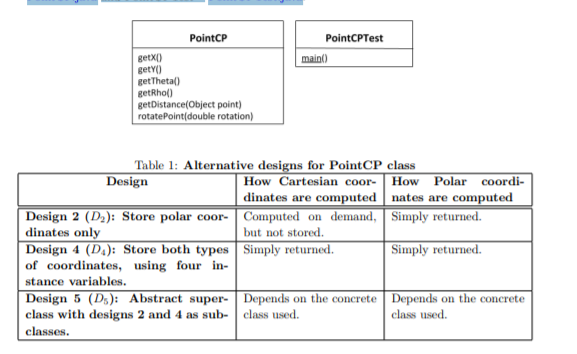
Equations (1) (4) show expressions for converting between attributes of Polar (i.e., 0 r 0 and 00 ) and its counterpart - Cartesian (i.e., 0x 0 and 0y 0 ) coordinates. In the figure below, we provide class designs of PointCP and PointCPTest whose implementations can be downloaded from: PointCP PointCP.java and PointCPTest PointCPTest.java

You are required to do the following:

(a) Modify the original implementation of PointCP.java to reflect distinct design specifications in Table 1. In particular, you will end up with 4 different implementations (say D2, D4, D52, D54). Do not modify implementations of methods - getDistance(...) and rotateP oint(...) for any of the design considerations (leave as-is). You are to hand-in a working code for each of the implementations that you have written. [20 points]

(b) Modify the downloaded version of PointCPTest.java accordingly to allow you test all the designs you have developed and write a brief report on your experiment. For each implementation, you may have different test file. You are to study execution times (in milliseconds) with implementations of rotatePoint(double rotation) and getDistance(Object point) for all the designs at different loop sizes and for at least six different runs. (see Listing 1 on how to setup your timer object) [20 points

2. Arrays : Compare the performance of ArrayList, Vector and ordinary arrays. You should do a series of experiments where you do each of the following tests with the three types of collection, timing the execution of each run. You should run each case several times on the same computer to obtain stable average timings.

You are required to do the following:

(a) Construct very large collections by putting random integers into each collection one at a time. The random integers should range in value from zero to nine. You should make each collection large enough so that the running time takes at least 10 seconds to add the integers in the case of an ArrayList. You will have to do some initial experiments to find out what is a good size. You would use the same size of elements for ArrayList, Vector and the array. The ArrayList and Vector can be created by successively adding items and allowing them to grow, while the array has to be created at its full size and then populated with its contents. You could also try to experiment with the case where you do create the ArrayList and Vector initially with their full size.

(b) Construct very large collections as in (a). Then use iterators to sum the elements. Subtract the construction time to get a measure of how much time the iteration takes. Use a for loop for the array, and an Iterator for the Vector and ArrayList. You are required to report your findings, conclusions and recommendations for developers, while presenting your data in tabular and visual formats.

r= 22 + y2. =tan(/), x=ricose, y=r sine (1) (2) (3) PointCPTest main) PointCP getxo) gety get Theta) getRhod) get Distance(Object point) rotatePoint(double rotation) Table 1: Alternative designs for PointCP class Design How Cartesian coor- How Polar coordi- dinates are computed nates are computed Design 2 (D): Store polar coor Computed on demand, Simply returned. dinates only but not stored. Design 4 (D): Store both types Simply returned. Simply returned. of coordinates, using four in- stance variables. Design 5 (Ds): Abstract super-Depends on the concrete Depends on the concrete class with designs 2 and 4 as sub- class used. class used. classes. r= 22 + y2. =tan(/), x=ricose, y=r sine (1) (2) (3) PointCPTest main) PointCP getxo) gety get Theta) getRhod) get Distance(Object point) rotatePoint(double rotation) Table 1: Alternative designs for PointCP class Design How Cartesian coor- How Polar coordi- dinates are computed nates are computed Design 2 (D): Store polar coor Computed on demand, Simply returned. dinates only but not stored. Design 4 (D): Store both types Simply returned. Simply returned. of coordinates, using four in- stance variables. Design 5 (Ds): Abstract super-Depends on the concrete Depends on the concrete class with designs 2 and 4 as sub- class used. class used. classes