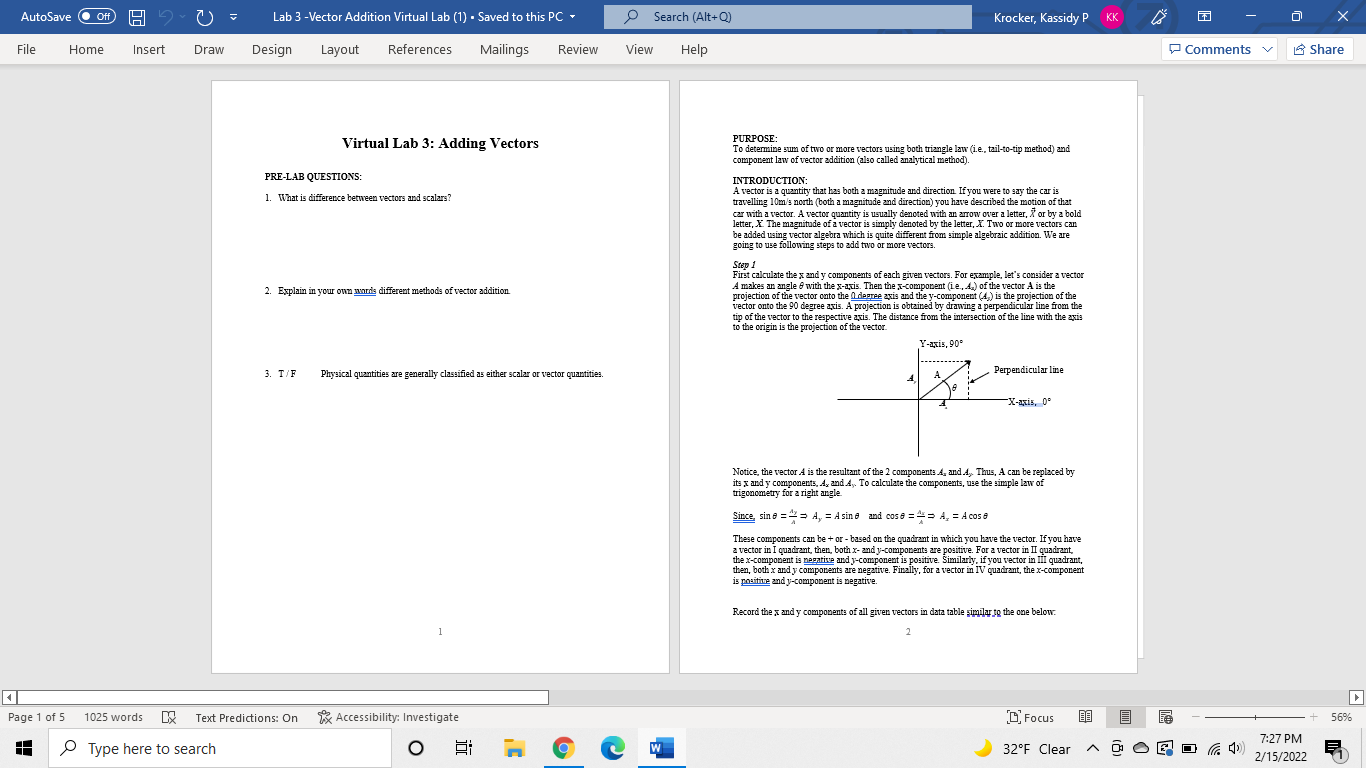
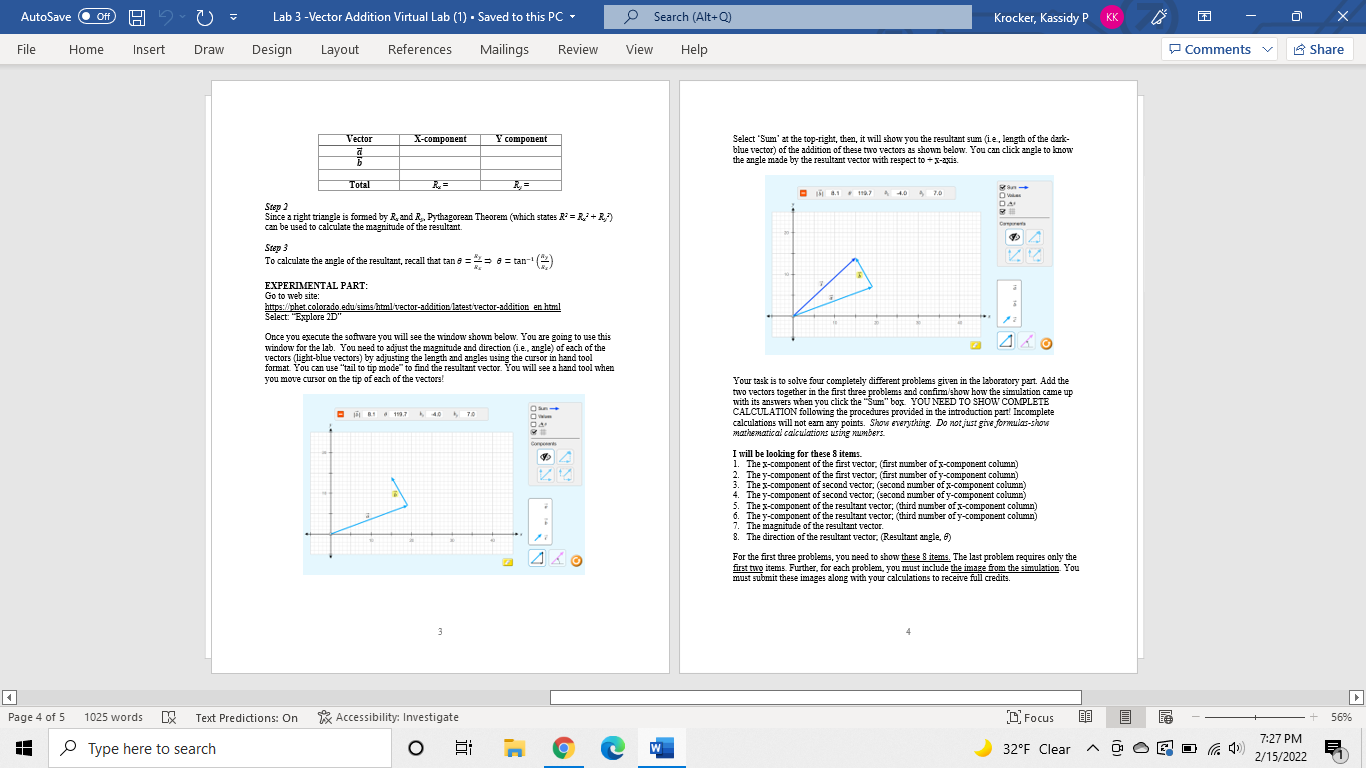
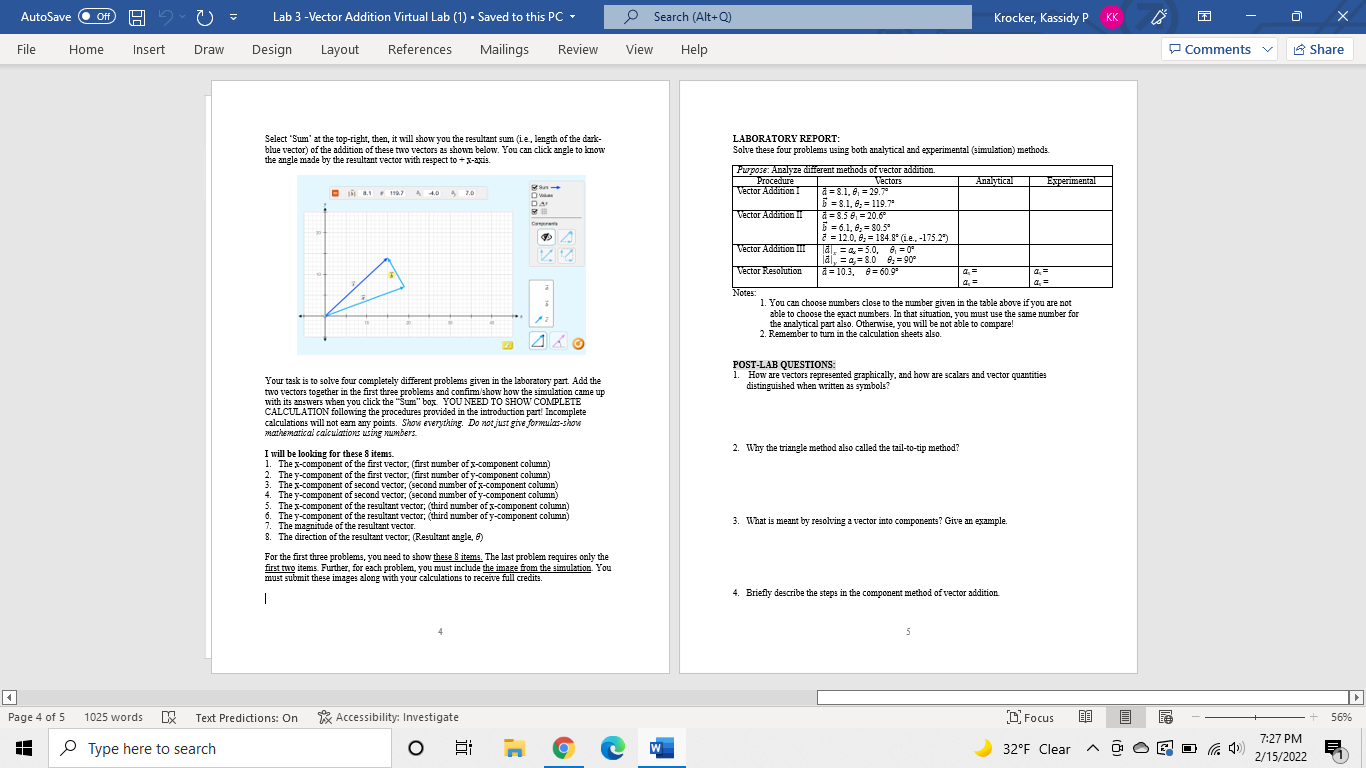
AutoSave O Off) 15 - 7) - Lab 3 -Vector Addition Virtual Lab (1) . Saved to this PC . Search (Alt+Q) Krocker, Kassidy P KK X File Home Insert Draw Design Layout References Mailings Review View Help Comments Share Virtual Lab 3: Adding Vectors PURPOSE To determine sum of two or more vectors using both triangle law (i.e., tail-to-tip method) and component law of vector addition (also called analytical method). PRE-LAB QUESTIONS: INTRODUCTION: 1. What is difference between vectors and scalars? A vector is a quantity that has both a magnitude and direction. If you were to say the car is travelling 10m/: north (both a magnitude and direction) you have described the motion of that car with a vector. A vector quantity is usually denoted with an arrow over a letter, N' or by a bold letter, X The magnitude of a vector is simply denoted by the letter, X. Two or more vectors can be added using vector algebra which is quite different from simple algebraic addition. We are going to use following steps to add two or more vectors. Step 1 First calculate the x and y components of each given vectors. For example, let's consider a vector 2. Explain in your own words different methods of vector addition. A makes an angle & with the x-axis. Then the x-component (ie., 4.) of the vector A is the projection of the vector onto the O degree axis and the y-component (4 ) is the projection of the vector onto the 90 degree axis. A projection is obtained by drawing a perpendicular line from the tip of the vector to the respective axis. The distance from the intersection of the line with the axis to the origin is the projection of the vector. 3. T/F Physical quantities are generally classified as either scalar or vector quantities. Perpendicular line X-axis, 0" Notice, the vector A is the resultant of the 2 components.4, and.4,. Thus, A can be replaced by its x and y components, A, and Ay. To calculate the components, use the simple law of trigonometry for a right angle. Since, sin # = = = A, = Asind and cose = = => A, = A cos # These components can be + or - based on the quadrant in which you have the vector. If you have a vector in I quadrant, then, both x- and J-components are positive. For a vector in II quadrant, the x-component is negative and y-component is positive. Similarly, if you vector in III quadrant, then, both x and y components are negative. Finally, for a vector in IV quadrant, the x-component is positive and y-component is negative Record the x and y components of all given vectors in data table similar to the one below. Page 1 of 5 1025 words x Text Predictions: On % Accessibility: Investigate ( Focus 56% 7:27 PM Type here to search O W 32'F Clear ~ 0 0 6 0 ( (), 2/15/2022AutoSave O Off) 15 - 7) - Lab 3 -Vector Addition Virtual Lab (1) . Saved to this PC . Search (Alt+Q) Krocker, Kassidy P KK X File Home Insert Draw Design Layout References Mailings Review View Help Comments Share Vector X-component Y component Select "Sum' at the top-right, then, it will show you the resultant sum (ie, length of the dark- blue vector) of the addition of these two vectors as shown below. You can click angle to know the angle made by the resultant vector with respect to + x-axis. Total R RE 15 8.1 + 1987 4 4.0 4 7.0 gan - Step 2 DA Since a right triangle is formed by R. and R,, Pythagorean Theorem (which states R' = R./ + R.) can be used to calculate the magnitude of the resultant. Step 3 To calculate the angle of the resultant, recall that tan s = = = 6 = tan-: (2) EXPERIMENTAL PART: Go to web site: http::/phet.colorado.edu/sims/html/vector-addition/latest vector-addition en html Select: "Explore 2D" Once you execute the software you will see the window shown below. You are going to use this window for the lab. You need to adjust the magnitude and direction (i.e., angle) of each of the 4 40 vectors (light-blue vectors) by adjusting the length and angles using the cursor in hand tool format. You can use "tail to tip mode" to find the resultant vector. You will see a hand tool when you move cursor on the tip of each of the vectors! Your tack is to solve four completely different problems given in the laboratory part. Add the two vectors together in the first three problems and confirm/show how the simulation came up with its answers when you click the "Sum" box. YOU NEED TO SHOW COMPLETE CALCULATION following the procedures provided in the introduction part! Incomplete calculations will not earn any points. Show everything. Do not just give formulas-show mathematical calculations ving numbers I will be looking for these & items. 1. The x-component of the first vector, (first number of x-component column) The y-component of the first vector, (first mum mmber of y-component column) The x-component of second vector; (second number of x-component column) The y-component of second vector, (second number of y-component column) . The x-component of the resultant vector; (third number of x-component column) The y-component of the resultant vector; (third number of y-component column) 7. The magnitude of the resultant vector. 8. The direction of the resultant vector, (Resultant angle, e) For the first three problems, you need to show these & items. The last problem requires only the first two items. Further, for each problem, you must include the image from the simulation. You must submit these images along with your calculations to receive full credits. Page 4 of 5 1025 words DX Text Predictions: On % Accessibility: Investigate [ Focus 56% 7:27 PM Type here to search O W 32'F Clear ~ 9 0 6 0 ((), 2/15/2022AutoSave O Off) 15 - 7) - Lab 3 -Vector Addition Virtual Lab (1) . Saved to this PC . Search (Alt+Q) Krocker, Kassidy P KK X File Home Insert Draw Design Layout References Mailings Review View Help Comments Share Select "Sum' at the top-right, then, it will show you the resultant sum (ie, length of the dark- LABORATORY REPORT: blue vector) of the addition of these two vectors as shown below. You can click angle to know Solve these four problems using both analytical and experimental (simulation) methods. the angle made by the resultant vector with respect to + x-1X]:. Purpose: Analyze different methods of vector addition. Procedure Vectors Analytical Experimental 151 8.1 4 1987 4 4.0 4 70 Vector Addition I a = 8.1. 81 = 29.79 B =8.1, 8, = 119.7 Vector Addition II a = 8.5 91 = 20.6- 6 = 6.1, 8, = 80.5" = 12.0, 8, = 184 8" (i.e., -175.2") Vector Addition III , = =5.0, 8 =0' lal, = a,= 8.0 4,=90 Vector Resolution a = 10.3. 8= 60.93 Notes: 1. You can choose numbers close to the number given in the table above if you are not able to choose the exact numbers. In that situation, you must use the same number for the analytical part also. Otherwise, you will be not able to compare! 410 2. Remember to tum in the calculation sheets also. POST-LAB QUESTIONS: Your task is to solve four completely different problems given in the laboratory part. Add the How are vectors represented graphically, and how are scalars and vector quantities two vectors together in the first three problems and confirm show how the simulation came up distinguished when written as symbols? with its answers when you click the "Sum" box. YOU NEED TO SHOW COMPLETE CALCULATION following the procedures provided in the introduction part! Incomplete calculations will not ear any points. Show everything. Do not just give formulas-show mathematical calculations ving numbers. I will be looking for these 8 items. 2. Why the triangle method also called the tail-to-tip method? 1. The x-component of the first vector, (first number of x-component column) 2. The y-component of the first vector, (first number of y-component column) . The x-component of second vector; (second number of x-component column) . They-component ment of second vector; (second number of y-component column) 3. The x-component of the resultant vector; (third number of x-component column) . The y-component of the resultant vector; (third number of y-component column) 7. The magnitude of the resultant vector. 3. What is meant by resolving a vector into components? Give an example. B. The direction of the resultant vector. (Resultant angle, a) For the first three problems, you need to show these & items. The last problem requires only the first two items. Further, for each problem, you must include the image from the simulation. You must submit these images along with your calculations to receive full credits. 4. Briefly describe the steps in the component method of vector addition 5 Page 4 of 5 1025 words DX Text Predictions: On % Accessibility: Investigate [ Focus 56% Type here to search O W 7:27 PM 32'F Clear ^ 0 0 B D ( (), 2/15/2022